Functions Inverse functions and composition
Course administration
Midterm:
• Wednesday, February 15, 2006
• Closed book, in-class
• Covers Chapter 1 of the textbook
Homework 4 is out
• Due on Friday, February 10, 2006
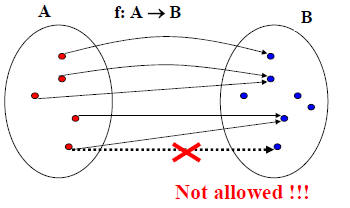
• Definition: Let A and B be two sets. A function from A to B,
denoted f: A → B , is an assignment of exactly one element of
B to each element of A. We write f(a) = b to denote the
assignment of b to an element a of A by the function f.
Injective function
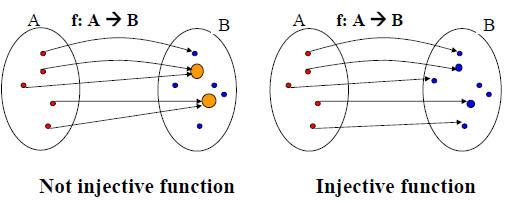
Definition: A function f is said to be one-to-one, or injective,
if
and only if f(x) = f(y) implies x = y for all x, y in the domain of
f. A function is said to be an injection if it is one-to-one.
Alternate: A function is one-to-one if and only if f(x) ≠ f(y),
whenever x ≠ y. This is the contrapositive of the definition.
Surjective function
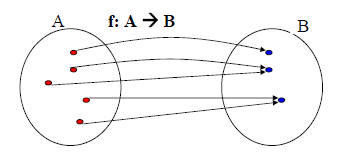
Definition: A function f from A to B is called onto, or surjective,
if and only if for every b ∈ B there is an element a ∈ A such that
f(a) = b.
Alternative: all co-domain elements are covered
Bijective functions
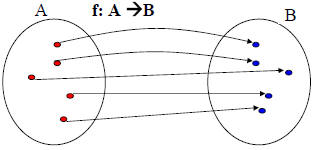
Definition: A function f is called a bijection if it is both
one-to-one
and onto.
• Let f be a function from a set A to itself, that is
f: A->A
Assume
• A is finite and f is one-to-one (injective)
• Is f an onto function (surjection)?
• Let f be a function from a set A to itself, that is
f: A->A
Assume
• A is finite and f is one-to-one (injective)
• Is f an onto function (surjection)?
• Yes. Every element points to exactly one element. Injection
assures they are different . So we have |A| different elements A
points to. Since f:A->A the co-domain is covered thus the
function is also a surjection (and bijection)
• A is finite and f is an onto function
• Is the function one-to-one?
• Let f be a function from a set A to itself, that is
f: A->A
Assume
• A is finite and f is one-to-one (injective)
• Is it an onto function (surjection)?
• Yes. Every element points to exactly one element. Injection
assures they are different . So we have |A| different elements A
points to. Since f: A -> A the co-domain is covered thus the
function is also a surjection (and bijection)
• A is finite and f is an onto function
• Is the function one-to-one?
• Yes. Every element maps to exactly one element and all elements
in A are covered. Thus the mapping must be one-to-one
Functions on real numbers
Definition: Let f1 and f2 be functions from A to R (reals). Then
f1 + f2 and f1 * f2 are also functions from A to R defined by
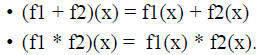
Examples:
• Assume
• f1(x) = x - 1
• f2(x) = x3 + 1
then
• (f1 + f2)(x) = x3 + x
• (f1 * f2)(x) = x4 - x3 + x - 1.
Increasing and decreasing functions
Definition: A function f whose domain and codomain
are subsets
of real numbers is strictly increasing if f(x) > f(y) whenever x >
y and x and y are in the domain of f. Similarly, f is called
strictly decreasing if f(x) < f(y) whenever x > y and x and y are
in the domain of f.
Note: Strictly increasing and strictly decreasing functions are one-to-one.
Example:
• Let g : R → R, where g(x) = 2x - 1. Is it increasing ?
Definition: A function f whose domain and codomain are subsets
of real numbers is strictly increasing if f(x) > f(y) whenever x >
y and x and y are in the domain of f. Similarly, f is called
strictly decreasing if f(x) < f(y) whenever x > y and x and y are
in the domain of f.
Note: Strictly increasing and strictly decreasing functions are one-to-one (injective).
Example:
• Let g : R → R, where g(x) = 2x - 1. Is it increasing ?
• Proof .
For x>y holds 2x > 2y and subsequently 2x-1 > 2y-1
Thus g is strictly increasing.
Definition: Let A be a set. The identity function on A is the
function iA: A → A where iA(x) = x.
Example:
• Let A = {1,2,3}
Then:
• iA(1) = ?
Definition: Let A be a set. The identity function on A is the
function iA: A → A where iA(x) = x.
Example:
• Let A = {1,2,3}
Then:
• iA(1) = 1
• iA(2) = ?
Definition: Let A be a set. The identity function on A is the
function iA: A → A where iA(x) = x.
Example:
• Let A = {1,2,3}
Then:
• iA(1) = 1
• iA(2) = 2
• iA(3) = 3.
Bijective functions
Definition: A function f is called a bijection if it is both one-to-one and onto.
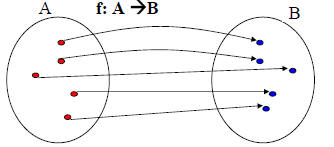
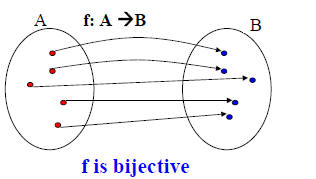
Inverse functions
Definition: Let f be a bijection from set A to set B. The inverse
function of f is the function that assigns to an element b from B
the unique element a in A such that f(a) = b. The inverse
function of f is denoted by f-1. Hence, f-1(b) = a, when f(a) = b.
If the inverse function of f exists, f is called invertible.
Note: if f is not a bijection then it is not possible to define the
inverse function of f.
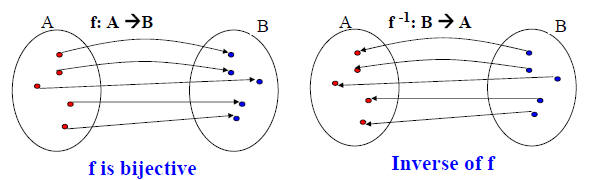
Definition: Let f be a bijection from set A to set B. The inverse
function of f is the function that assigns to an element b from B
the unique element a in A such that f(a) = b. The inverse
function of f is denoted by f-1. Hence, f-1(b) = a, when
f(a) = b.
If the inverse function of f exists, f is called invertible.
Note: if f is not a bijection then it is not possible to define the
inverse function of f.
Example 1:
• Let A = {1,2,3} and iA be the identity function

• Therefore, the inverse function of iA is iA.
Inverse functions
Example 2:
• Let g : R → R, where g(x) = 2x - 1.
• What is the inverse function g-1 ?
Approach to determine the inverse:
y = 2x - 1 => y + 1 = 2x
=> (y+1)/2 = x
• Define g-1(y) = x= (y+1)/2
Test the correctness of inverse:
• g(3) = ..
Example 2:
• Let g : R → R, where g(x) = 2x - 1.
• What is the inverse function g-1 ?
Approach to determine the inverse:
y = 2x - 1 => y + 1 = 2x
=> (y+1)/2 = x
• Define g-1(y) = x= (y+1)/2
Test the correctness of inverse:
• g(3) = 2*3 - 1 = 5
• g-1 (5) =
Example 2:
• Let g : R → R, where g(x) = 2x - 1.
• What is the inverse function g-1 ?
Approach to determine the inverse:
y = 2x - 1 => y + 1 = 2x
=> (y+1)/2 = x
• Define g-1(y) = x= (y+1)/2
Test the correctness of inverse:
• g(3) = 2*3 - 1 = 5
• g-1 (5) = (5+1)/2 = 3
• g(10) =
Example 2:
• Let g : R → R, where g(x) = 2x - 1.
• What is the inverse function g-1 ?
Approach to determine the inverse:
y = 2x - 1 => y + 1 = 2x
=> (y+1)/2 = x
• Define g-1(y) = x= (y+1)/2
Test the correctness of inverse:
• g(3) = 2*3 - 1 = 5
• g-1 (5) = (5+1)/2 = 3
• g(10) = 2*10 - 1 = 19
• g-1 (19) =
Example 2:
• Let g : R → R, where g(x) = 2x - 1.
• What is the inverse function g-1 ?
Approach to determine the inverse:
y = 2x - 1 => y + 1 = 2x
=> (y+1)/2 = x
• Define g-1(y) = x= (y+1)/2
Test the correctness of inverse:
• g(3) = 2*3 - 1 = 5
• g-1 (5) = (5+1)/2 = 3
• g(10) = 2*10 - 1 = 19
• g-1 (19) = (19+1)/2 = 10.
Composition of functions
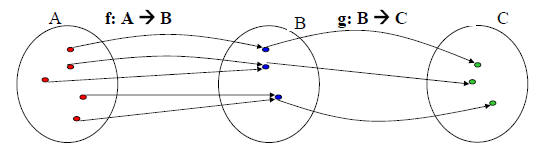
Definition: Let f be a function from set A to set B and let g be a
function from set B to set C. The composition of the functions
g and f, denoted by g 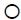 f is defined by
f is defined by
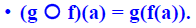
Example 1:
• Let A = {1,2,3} and B = {a,b,c,d}
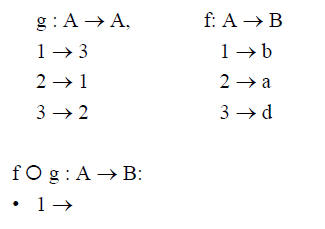
Example 1:
• Let A = {1,2,3} and B = {a,b,c,d}
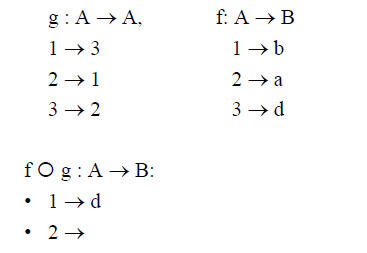
Example 1:
• Let A = {1,2,3} and B = {a,b,c,d}
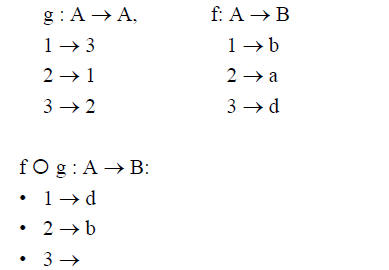
Example 1:
• Let A = {1,2,3} and B = {a,b,c,d}
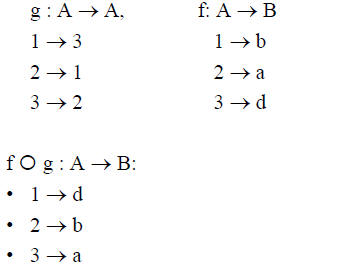
Example 2:
• Let f and g be function from Z into Z, where
• f(x) = 2x and g(x) = x^2
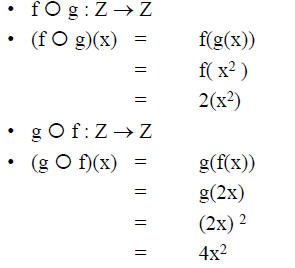
Example 3:
• (f  f-1 )(x) = x and (f-1
f-1 )(x) = x and (f-1  f)(x) = x, for all x.
f)(x) = x, for all x.
• Let f : R → R, where f(x) = 2x – 1 and f-1 (x) = (x+1)/2.
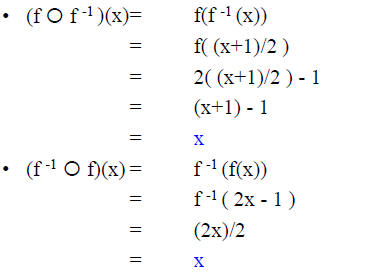
Some functions
Definitions:
• The floor function assigns a real number x the largest integer
that is less than or equal to x. The floor function is denoted by
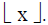
• The ceiling function assigns to the real number x the smallest
integer that is greater than or equal to x. The ceiling function is
denoted by 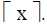
Other important functions:
• Factorials : n! = n(n-1) such that 1! = 1
| Prev | Next |