Floating-Point vs. Fixed-Point Numbers
• Fixed point has limitations
 x = 0000 0000. 0000 10012 x = 0000 0000. 0000 10012
 y = 1001 0000.
0000 00002 y = 1001 0000.
0000 00002
 Rounding? Rounding?
 Overflow? (x2
and y2 under/overflow) Overflow? (x2
and y2 under/overflow)
• Floating point: represent numbers in two fixed -width
fields: “magnitude” and “exponent”
 Magnitude: more
bits = more accuracy Magnitude: more
bits = more accuracy
 Exponent: more
bits = wider range of numbers Exponent: more
bits = wider range of numbers
| |
± |
Exponent |
Magnitude |
| X = |
 |
|
Floating Point Number Representation
• Sign field:
 When 0:
positive number, when 1, negative When 0:
positive number, when 1, negative
• Exponent:
 Usually
presented as unsigned by adding an offset Usually
presented as unsigned by adding an offset
 Example: 4 bits
of exponent, offset=8 Example: 4 bits
of exponent, offset=8
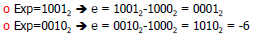
• Magnitude (also called significand, mantissa)
 Shift the
number to get: 1.xxxx Shift the
number to get: 1.xxxx
 Magnitude is
the fractional part (hidden ‘1’) Magnitude is
the fractional part (hidden ‘1’)
 Example: 6 bits
of mantissa Example: 6 bits
of mantissa
o Number=110.0101 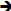 shift: 1.100101 shift: 1.100101
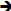 mantissa=100101 mantissa=100101
o Number=0.0001011 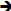 shift: 1.011 shift: 1.011
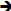 mantissa=011000 mantissa=011000 |
Floating Point Numbers: Example
| |
± |
Exponent |
Magnitude |
 |
|
| Floating Point Number Range
• Range: [-max, -min] U [min, max]
 Min = smallest
magnitude Min = smallest
magnitude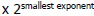
 Max = largest
magnitude Max = largest
magnitude 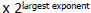
• What happens if:
 We increase #
bits for exponent? We increase #
bits for exponent?
 Increase # bits
for magnitude? Increase # bits
for magnitude?
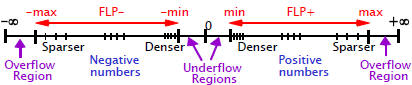
|
| Floating Point Operations
• Addition/subtraction, multiplication/division,
function evaluations, ...
• Basic operations
 Adding
exponents / magnitudes Adding
exponents / magnitudes
 Multiplying
magnitudes Multiplying
magnitudes
 Aligning
magnitudes (shifting, adjusting the Aligning
magnitudes (shifting, adjusting the
exponent)
 Rounding Rounding
 Checking for
overflow/underflow Checking for
overflow/underflow
 Normalization
(shifting, adjusting the exponent) Normalization
(shifting, adjusting the exponent) |
| Floating Point Addition
• More difficult than multiplication!
• Operations:
 Align magnitudes (so that exponents are equal ) Align magnitudes (so that exponents are equal )
 Add (and round) Add (and round)
 Normalize (result in the form of 1.xxx) Normalize (result in the form of 1.xxx)
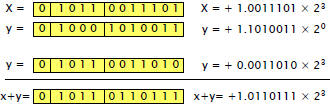
|
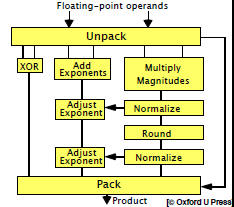
| Floating Point Adder Architecture
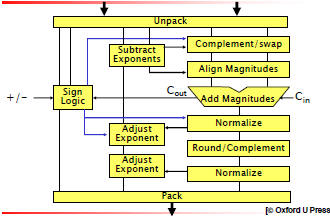 |
| Floating Point Adder Components
• Unpacking
 Inserting the “hidden 1” Inserting the “hidden 1”
 Checking for special inputs (NaN, zero) Checking for special inputs (NaN, zero)
• Exponent difference
 Used in aligning the magnitudes Used in aligning the magnitudes
 A few bits enough for subtraction A few bits enough for subtraction
o If 32-bit magnitude adder, 8 bits of exponent, only 5 bits
involved in subtraction
 If negative difference , swap, use positive diff If negative difference , swap, use positive diff
o How to compute the positive diff?
• Pre-shifting and swap
 Shift/complement provided for one operand only Shift/complement provided for one operand only
 Swap if needed Swap if needed |
|
• Rounding
 Three extra bits used for rounding Three extra bits used for rounding
• Post-shifting
 Result in the range (-4, 4) Result in the range (-4, 4) 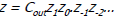
 Right shift: 1 bit max Right shift: 1 bit max
o If 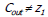 right shift right shift
 Left shift: up to # of bits in magnitude Left shift: up to # of bits in magnitude
o Determine # of consecutive 0’s (1’s) in z, beginning with z1.
 Adjust exponent accordingly Adjust exponent accordingly
• Packing
 Check for special results (zero, under-/overflow) Check for special results (zero, under-/overflow)
 Remove the hidden 1 Remove the hidden 1 |
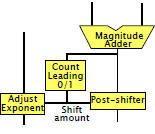
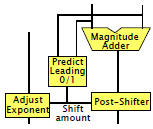
Counting vs. Predicting Leading Zeros/Ones
 |
 |
Counting:
Simpler but on the
critical path |
Predicting:
More complex
architecture |
|
| Floating Point Multiplication
• Simpler than floating-point addition
• Operation:
 Inputs: Inputs: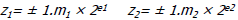
 Output = Output = 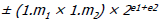
 Sign: XOR Sign: XOR
 Exponent: Exponent:
o Tentatively computed as e1+e2
o Subtract the bias (=127) HOW?
o Adjusted after normalization
 Magnitude Magnitude
o Result in the range [1,4) (inputs in the range [1,2) )
o Normalization: 1- or 2-bit shift right, depending on rounding
o Result is 2.(1+m) bits, should be rounded to (1+m) bits
o Rounding can gradually discard bits, instead of one last stage |
Floating Point Multiplier Architecture
Note:
Pipelining is
used in
magnitude
multiplier, as
well as block
boundaries |
 |
|
| Square-Rooting • Most
important elementary function
• In IEEE standard, specified a basic operation
(alongside +,-,*,/)
• Very similar to division
• Pencil-and-paper method:
 Radicand: Radicand: 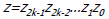
 Square root : Square root : 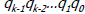
 Remainder Remainder 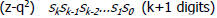 |
| Square Rooting: Example
• Example: sqrt(9 52 41)
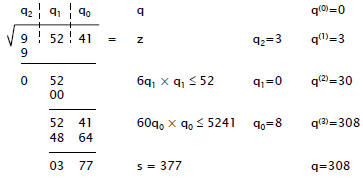
|
|
• Why double the partial root?
 Partial root after step 2 is: Partial root after step 2 is: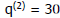
 Appending the next digit Appending the next digit 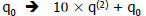
 Square of which is 1 Square of which is 1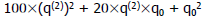
 The term The term 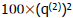 already subtracted already subtracted
 Find q0 such that Find q0 such that 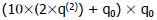 is the is the
max number ≤ partial remainder
• The binary case:
 Square of Square of 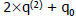 is: is:
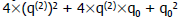
 Find q0 such that Find q0 such that 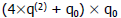 is ≤ partial is ≤ partial
remainder
 For For 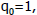 the expression becomes the expression becomes
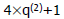 (i.e., (i.e.,
append “01” to the partial root) |
| Square Rooting: Example Base 2
• Example: sqrt(011101102) = sqrt(118)
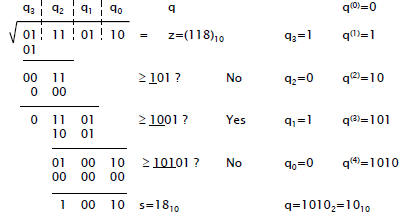
|
| Sequential Shift/Subtract Square Rooter
Architecture
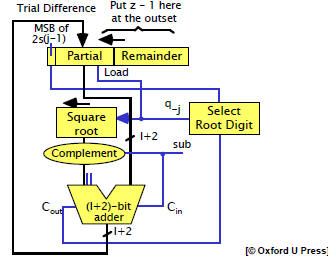 |
| Other Methods for Square Rooting
• Restoring vs. non-restoring
 We looked at the restoring algorithm We looked at the restoring algorithm
(after subtraction, restore partial remainder if the
result is negative)
 Non-restoring: Non-restoring:
Use a different encoding (use digits {-1,1} instead of
{0,1}) to avoid restoring
• High-radix
 Similar to modified Booth encoding multiplication: take Similar to modified Booth encoding multiplication: take
care of more number of bits at a time
 More complex circuit , but faster More complex circuit , but faster |
|
• Convergence methods
 Use the Newton method to approximate the function Use the Newton method to approximate the function
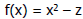 approximates approximates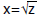
OR
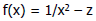 approximates approximates
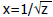 , ,
multiply by z to get 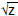
 Iteratively improve the accuracy Iteratively improve the accuracy
 Can use lookup table for the first iteration Can use lookup table for the first iteration |
| Square Rooting: Abstract Notation
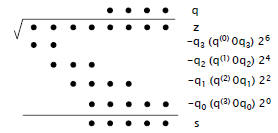
Floating point format:
- Shift left (not right)
- Powers of 2 decreasing |
| Restoring Floating-Point Square Root Calc.
 |
 |
| Nonrestoring Floating-Point Square Root Calc.
 |

If final S negative, drop the last ‘1’ in q, and
restore the
remainder to the last positive value. |
| Square Root Through Convergence
• Newton-Rapson method:
 Choose Choose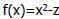
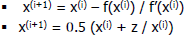
• Example: compute square root of
z=(2.4)10
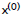 read
out from table = 1.5 read
out from table = 1.5 |
accurate to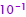 |
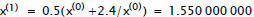 |
accurate to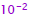 |
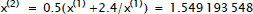 |
accurate to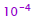 |
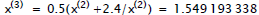 |
accurate to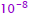 |
|
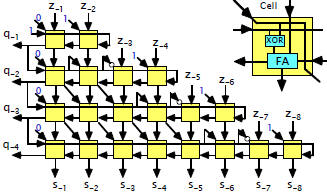
| Non-Restoring Parallel Square Rooter
 |
| Function Evaluation
•
We looked at square root calculation
 Direct hardware implementation (binary, BSD, high-radix) Direct hardware implementation (binary, BSD, high-radix)
o Serial
o Parallel
 Approximation (Newton method) Approximation (Newton method)
• What about other functions?
 Direct implementation Direct implementation
o Example: 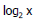 can be directly
implemented in hardware can be directly
implemented in hardware
(using square root as a sub-component)
 Polynomial approximation Polynomial approximation
 Table look-up Table look-up
o Either as part of calculation or for the full calculation |
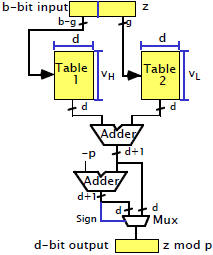
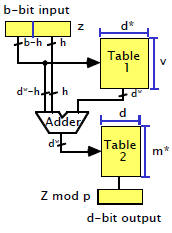
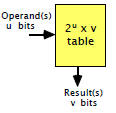
Table Lookup
 |
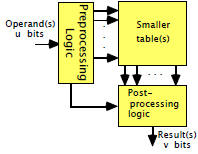 |
Direct table-lookup
implementation |
Table-lookup with pre-and
post-processing |
|
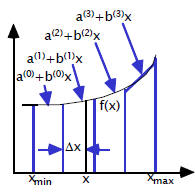
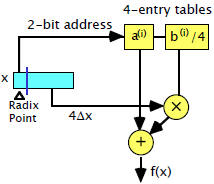
Linear Interpolation Using Four Subinterval
|
Piecewise Table Lookup
|
| Accuracy vs. Lookup Table Size Trade-off
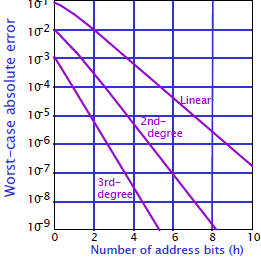 |
 x = 0000 0000. 0000 10012
x = 0000 0000. 0000 10012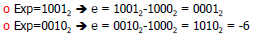
 shift: 1.100101
shift: 1.100101
 mantissa=100101
mantissa=100101 shift: 1.011
shift: 1.011
 mantissa=011000
mantissa=011000

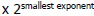
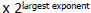

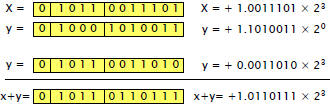

 right shift
right shift

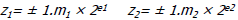
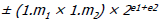

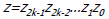
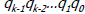
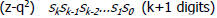
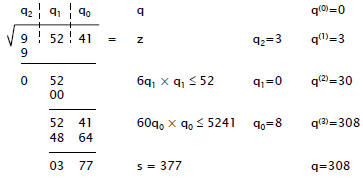
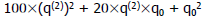
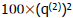 already subtracted
already subtracted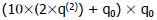 is the
is the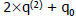 is:
is: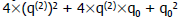
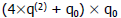 is ≤ partial
is ≤ partial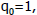 the
the 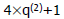 (i.e.,
(i.e.,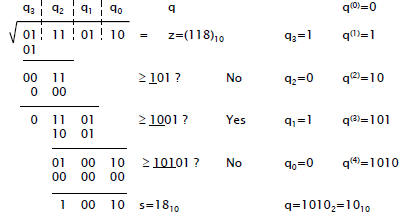

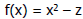 approximates
approximates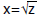
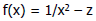 approximates
approximates
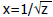 ,
,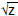





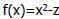
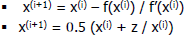
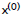 read
out from table = 1.5
read
out from table = 1.5
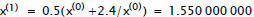
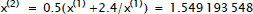
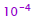
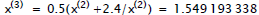
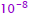

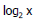 can be directly
implemented in hardware
can be directly
implemented in hardware