Get it on Google Play Get it on Apple Store

GEOMETRY DEFINITIONS

THEOREMS

Theorem 1. When two lines cross,

(a) adjacent angles add up to 180° , and

(b) vertical angles are equal.

Theorem 2. Suppose that ℓ and m are two lines crossed by a transversal.

(a) If ℓ and m are parallel, then both pairs of alternate interior angles are equal. If at
least one pair of alternate interior angles are equal, then ℓ and m are parallel.

(b) If ℓ and m are parallel, then each pair of interior angles on the same side of the
transversal adds up to 180° . If at least one pair of interior angles on the same side
of the transversal adds up to 180° , then ℓ and m are parallel.

(c) If ℓ and m are parallel, then each pair of exterior angles on the same side of the
transversal adds up to 180° . If at least one pair of exterior angles on the same side
of the transversal adds up to 180° , then ℓ and m are parallel.
 

Theorem 3. The angles of a triangle add up to 180° .

Theorem 4. If two triangles ABC and DEF have ∠A = ∠D and ∠B = ∠E then also
∠C = ∠F.

Theorem 5. (a) If two sides of a triangle are equal then the opposite angles are equal.
(b) If two angles of a triangle are equal then the opposite sides are equal.

Theorem 6. In triangle ABC, if ∠B is a right angle then the area of the triangle is
1/2AB ∙ BC.

Theorem 7. The area of a triangle is one-half of the base times the height.

Theorem 8 (Pythagorean theorem). In a right triangle the sum of the squares of the
two legs is equal to the square of the hypotenuse .

Theorem 9 (Hypotenuse-Leg Theorem). In triangles ABC and DEF, if ∠A and ∠D
are right angles, and if BC = EF and AB = DE, then ΔABC 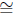ΔDEF. That is, if
two right triangles have the hypotenuse and a leg matching then they are congruent.

Theorem 10. If ABCD is a parallelogram then opposite sides of ABCD are equal.

Theorem 11. If ABCD is a parallelogram then opposite angles of ABCD are equal.

Theorem 12. If a quadrilateral has a pair of sides which are equal and parallel then it
is a parallelogram.

Theorem 13. A quadrilateral is a parallelogram 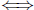the diagonals bisect each other
(that is, 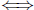the intersection of the two diagonals is the midpoint of each diagonal).

Theorem 14. (a) Suppose that C is a point on the segment AB. C is the midpoint of
AB 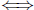AB = 2AC.
(b) A line segment can have only one midpoint.

Theorem 15. In triangle ABC, let D be the midpoint of AC and suppose that E is a
point on BC with DE parallel to AB. Then E is the midpoint of BC and DE = 1/2AB.

Theorem 16. In triangle ABC, let D be the midpoint of AC and let E be the midpoint
of BC. Then DE is parallel to AB and DE = (1/2)AB.

Theorem 17. [SAS for similarity] In triangles ABC and DEF, if ∠C = ∠F and
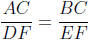then ΔABC ~ ΔDEF.

Theorem 18 (SSS for similarity). In triangles ABC and DEF, if
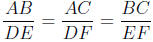
then ΔABC ~ ΔDEF.

Theorem 19. sin(∠ABC) = sin(180°  − ∠ABC)

Theorem 20. For any triangle ABC, the area can be calculated by any of the following
three formulas :

area of ΔABC = 1/2AB ∙ AC sin∠A

area of ΔABC = 1/2AB ∙ BC sin∠B

area of ΔABC = 1/2AC ∙ BC sin∠C

that is, the area is one half the product of two sides times the sine of the included angle.

Theorem 21 (Law of Sines). In any triangle ABC,

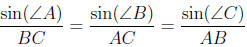
Theorem 22. For any triangle ABC, the perpendicular bisectors of AB, AC and BC
are concurrent.

Theorem 23. For any triangle ABC, the bisectors of ∠A, ∠B and ∠C are concurrent.

Theorem 24. For any triangle ABC, the three altitudes are concurrent.

Theorem 25. The point where two medians of a triangle intersect is 2/3 of the way
from each of the two vertices to the opposite midpoint.

Theorem 26. For any triangle ABC, the three medians are concurrent.

Theorem 27. Let ABC be any triangle. Let O be the circumcenter of ABC, let G be
the centroid of ABC, and let H be the orthocenter of ABC. Then O, G and H are
collinear.

Theorem 28 (Theorem of Menelaus). Let ABC be any triangle. Let A' be a point of
other than B and C, let B' be a point of 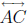other than A and C, and let C' be a
point of 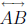other than A and B. If A', B' and C' are collinear then

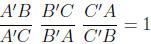
Theorem 29. The number 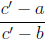is positive if C ' is outside of the segment AB and
negative if C ' is inside AB.

Theorem 30. The number 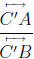is equal to 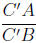if C' is outside of the segment AB and
is equal to 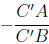if C' is inside the segment AB.

Theorem 31. Let ℓ be any line, and let C', C", A and B be points on ℓ, with A not the
same point as B. If 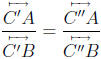then C' is the same point as C".

Theorem 32. Let ABC be a triangle. Let A' be a point of 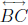other than B and C, let
B' be a point of 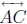other than A and C, and let C' be a point of 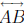other than A and
B. If A', B' and C' are collinear then

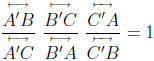
Theorem 33. Let ABC be a triangle. Let A' be a point of 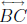other than B and C, let
B' be a point of 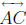other than A and C, and let C' be a point of 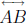other than A and
B. If

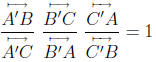
then A', B' and C' are collinear.

Theorem 34 (Theorem of Ceva). Let ABC be a triangle. Let A' be a point of 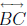other
than B and C, let B' be a point of 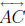other than A and C, and let C' be a point of
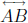
other than A and B. If 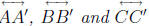are concurrent then

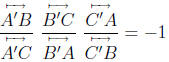
Theorem 35. Let ABC be a triangle. Let A' be a point of 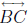other than B and C, let
B' be a point of 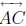other than A and C, and let C' be a point of 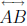other than A and
B. If

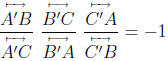
then 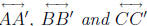are concurrent.

Theorem 36. Let A, B and C be points on a circle with center O.

(a) If B is outside of ∠AOC, then ∠ABC =(1/2)∠AOC.

(b) If B is inside of ∠AOC, then ∠ABC = 180° − (1/2)∠AOC.

Theorem 37. The arc cut off by a central angle is the same number of degrees as the
angle.

Theorem 38. Let A, B and C be points on a circle, and let ADC be the arc cut o by
∠ABC. Then

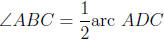
that is, the number of degrees in angle ABC is half the number of degrees in arc ADC.

Theorem 39. Let A, B, C and D be points on a circle and consider the angles ABC
and ADC.

(a) If ∠ABC and ∠ADC cut off the same arc, then ∠ABC = ∠ADC.

(b) If ∠ABC and ∠ADC do not cut o the same arc, then ∠ABC = 180° − ∠ADC.

Theorem 40. Let A, B, C and D be points on a circle, and suppose that the lines AB
and CD meet at a point P. Then PA ∙ PB = PC ∙ PD.

Theorem 41. Let C be a circle with center O, let A be a point on the circle, and let m
be a line through A. Then m is tangent to the circle m is perpendicular to OA.

Theorem 42. Let A and B be points on a circle, let C be a point on the tangent line at
B, and let ADB be the arc cut off by ∠ABC. Then
 

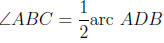
Prev Next