Introduction to Fractions
Learning Objectives
At the end of this lesson, you will be able to:
1. Understand what fractions are and what we use them for in everyday
workplace situations.
2. Understand how the concept of fractions is related to other math skills .
3. Understand how to perform simple mathematical operations with fractions.
4. Apply fractions to everyday workplace situations.
5. Write a fraction for a picture of a part of a whole or group.
6. Understand how to simplify both proper and improper fractions.
7. Understand how to add, subtract , multiply and divide fractions.
This lesson will include exercises on the simple computation of fractions as
well as
exercises that will help you to understand what the written forms of fractions
actually
represent. This lesson is not meant to teach you difficult computations of
fractions but
only introduce you to the concept of fractions and the different expressions of
fractions
that you may encounter in the workplace or your every day life.
Vocabulary and Key Terms
common denominator - A number into which all the denominators of a set of
fractions may be evenly divided.
denominator - The quantity below the line indicating the number of units
into which a
whole is divided.
divisor - The number that you are dividing by.
equivalent fractions - Two or more fractions that are of equal value such
as 4/8,
2/4, and ½.
fraction bar - The line that separates the numerator from the
denominator.
greater than symbol (>) - This is an arrow between two numbers that looks
like a
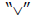 on its side and pointing toward the smaller
number. It is used to express the
on its side and pointing toward the smaller
number. It is used to express the
fact that one number is larger than the other number.
greatest common factor (GCF) - The largest number that will divide evenly
into
both the numerator and denominator of a fraction .
improper fraction - A fraction with a numerator (top number) equal to or
greater
than the denominator (bottom number).
invert - To turn upside down.
least common multiple ( LCM ) - The lowest number that two or more numbers
can
be divided into evenly.
less than symbol (<) - An arrow between two numbers that is pointing
toward the
smaller number. It is used to express the fact that one number is smaller than
the
other number.
lowest common denominator (LCD) - The lowest/smallest number that all
denominators will divide evenly into.
mixed number - A number consisting of a whole number and a fraction such
as 1½ or
3 1/8.
multiplication - Combining equal groups to get a total. The symbol “×”
(times) is
used to indicate multiplication.
numerator - This is the top number in a fraction.
proper fraction - A fraction where the top number is smaller than the
bottom
number.
reciprocal - The number turned upside down. The reciprocal of 4/1 is ¼.
Likewise,
the reciprocal of 3/5 is 5/3 and the reciprocal of 4/9 is 9/4. This is also
known as
inverting.
Prescription for Understanding
We use fractions when we want to name a part of something that is less than the
whole
or a group of items. One assumption that we make when we talk about fractions is
that
the whole or group that we are talking about is divided into equal parts. For
example,
we could divide a whole pie into six parts and to use a fraction of one sixth to
refer to
one of the pieces, then we are assuming that pie is divided into six equal
parts. We
may refer to one pencil in a group of ten pencils as being one tenth of the
group of
pencils, even though some of the pencils may be longer than the others. Observe
the
following two examples
PARTS OF A WHOLE
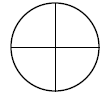
The circle above is divided into four equal parts that resemble a pie with four
large
pieces. Each so-called piece of the pie represents one fourth of the total pie.
Each
portion may also be written as 1/4 or sometimes be called a fourth.
PARTS OF A GROUP
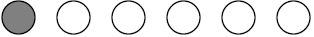
Since there are a total of six circles in the group above, the dark shaded
figure above
represents one sixth of the total group of figures. If each of the small circles
represents
balls then we could say that one of the balls is one sixth of the total group of
balls. We
could also express this part of the total group as 1/6 of the total group of
balls.
As health care providers, you will not be required to do any difficult math
operations
with fractions. You may need to understand and use the concept of fractions
while you
are performing your daily work. Since most of your activities do not require a
great deal
of computation, most of our exercises and skill practice will focus on the
understanding
of what fractions are, and how they are used in your work environment.
Proper Fractions
When working with proper fractions, it is important to simplify them or, in
other words,
reduce them to their lowest terms. To do this you need to find the Greatest
Common
Factor (GCF) for the numerator and the denominator. This is the greatest number
that
will divide into both the numerator and denominator.
Example: 40/60 will reduce to 2/3 by dividing both the numerator and the
denominator
by 20, which is the greatest common factor (GCF).
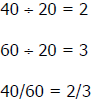
To reduce a fraction to its simplest form:
1. Find the GCF of the numerator and denominator
2. Divide both the numerator and denominator by the GCF.
Example: Find the simplest form of 10/15.
1. The GCF of 10 and 15 is 5.
2.
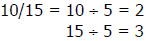
3. 2/3 is the simplest form.
Improper Fractions
When working with an improper fraction, remember to reduce it by making it a
mixed
number and then reducing the remainder by the GCF.
1. First change the fraction to a mixed numeral.
2. Then divide the numerator and denominator by the GCF.
Example: Find the simplified form of 6/4.
6/4 is reduced by making it a mixed number and then reducing the remainder by
dividing it by 2, the GCF. The whole number does not change when the fraction
is reduced to lowest terms.
6/4 = 1 2/4 2 ÷ 2 = 1 and 4 ÷ 2 = 2 Therefore 2/4 = ½ so 6/4 = 1½
Skill Check
Reduce each fraction to lowest terms, using the GCF.
1. 4/8 = __________
2. 10/15 = __________
3. 9/3 = __________
Circle the proper fraction in each pair.
4. ½ or 4/3
5. 6/7 or 7/6
6. 3/2 or 5/7
Change each improper fraction to a mixed numeral.
7. 7/3 = __________
8. 16/5 = __________
9. 18/7 = __________
10. 40/9 = __________
Addition of Fractions
When adding mixed numbers, find the Least Common Denominator (LCD) of the
fractions as needed. First add the fractions, then add the whole numbers. Reduce
the
fraction sum to lowest terms.
Problem: 1¼ + 2 7/8 = _______________
Step 1: Find the LCD. Since 4 can divide into 8, 8 is the common denominator
(you are looking for the smallest number that both of the denominators, 4 and
8, can divide into evenly, and not have a remainder.)
Step 2: Rename (change) the fraction to a fraction using a common
denominator:
Example: ¼ = 2/8
Step 3: Add the fractions and the whole numbers.
Example 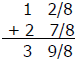
Step 4: If required, rename the improper fraction as a mixed number and
add.
Example: 3 9/8 = 3 + 1 1/8 = 4 1/8
Problem: 5 ¼ + 3 2/3 = _______________
Step 1: Find the LCD.
Example:
¼ + 2/3 = (1/4 × 3/3 ) + (2/3 × 4/4) =
3/12 + 8/12 = 11/12
Step 2: Rename (change) the fraction to a fraction using a common
denominator:
Example: ¼ = 3/ 12 and 2/3 = 8/12
Step 3: Add the fractions and the whole numbers.
Example: 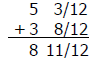
Step 4: If required, rename the improper fraction as a mixed number and
add.
Not required in this example because 8 11/12 is not an improper fraction.
Problem: 3 2/3 + 7 3/5 + 4 ¼ = _______________
Step 1: Find the LCD.
Example: 2/3 + 3/5 + ¼
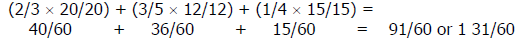
Step 2: Rename (change) the fractions(s) to a fraction using the common
denominator.
Example: 2/3 = 40/60 and 3/5 = 35/60 and ¼ = 15/60
Step 3: Add the fractions and the whole numbers.
Example: 3 40/60 + 7 36/60 + 4 15/60
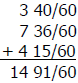
Step 4: If required, rename the improper fraction as a mixed number and
add.
Example: 14 91/60 or 14 + 1 31/60 = 15 31/60
Skill Check
11. 1 1/3 + 2 3/8 + 3 3/5 = _______________
12. 2 7/8 + 3¼ + 9 5/6 = _______________
13. 2 4/5 + 1 9/8 = _______________
14. 1 7/8 + 3½ + 5 1/9 = _______________
15. 1¾ + 2 1/8 + 1 5/7 = _______________
16. 1 3/5 + 2 1/3 + 3 3/8 = _______________
17. 2 9/8 + 1 4/5 = _______________
18. 1 1/8 + 2¾ + 1 5/7 = _______________
19. 2 5/6 + 3 7/8 + 9¼ = _______________
20. 1 1/9 + 3 7/8 +5½ = _______________
| Prev | Next |