Dividing Polynomials by Monomials

Write the following polynomials in Standard Form:





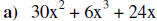
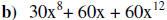
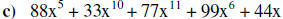
Determine the degree of the above polynomials:

a)
b)
c)

What is the leading coefficient of the above polynomials?

a)
b)
c)

Calculate the above polynomials accordingly and write them in standard form:

1.) a + b
2.) b - c
3.) a x b

Handout #1

Divide

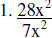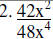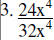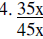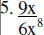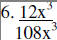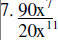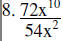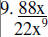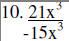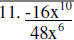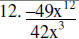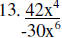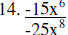Handout #2

Divide.

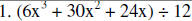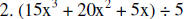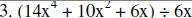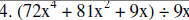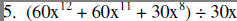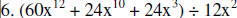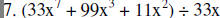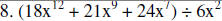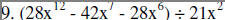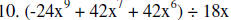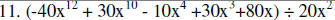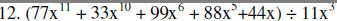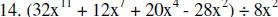Algebra Tiles Handout

Use algebra tiles to model division of polynomials .

Divide x ² + 4x + 4 by x + 3 using the following steps:

1) Use algebra tiles to model x² + 4x + 4. (Draw model below)

2) Use the tiles to create a length of x + 3. ( Draw below )

3) Keeping x + 3 as the length, try to create a rectangle that uses all the tiles from step
1. ( Draw below ) Explain whether or not all tiles can be used and why or why not.

Review Handout
(KEY)

Write the following polynomials in Standard Form:

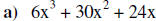
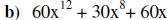
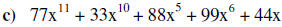
Determine the degree of the above polynomials:

a) Degree of 3.

b) Degree of 12.

c) Degree of 11.

What is the leading coefficient of the above polynomials:

a) Leading coefficient is 6.

b) Leading coefficient is 60.

c) Leading coefficient is 77.

Calculate the above polynomials accordingly and write them in standard form:

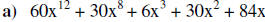
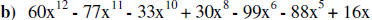
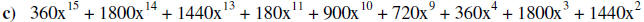
Handout #1
(KEY)

1.4	2.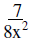
3.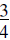	4.
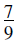5.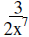	6.
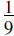7.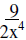	8.
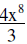9.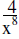	10.
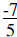11.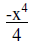	12.
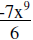13.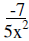	14.

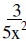Handout #2
(KEY)

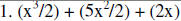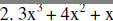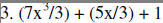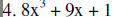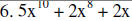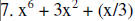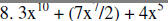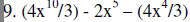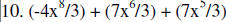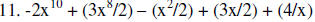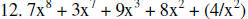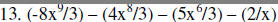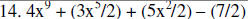Algebra Tiles Handout
(KEY)

Use algebra tiles to model division of polynomials .

Divide x² + 4x + 4 by x + 3 using the following steps:

4) Use algebra tiles to model x² + 4x + 4. (Draw model below)

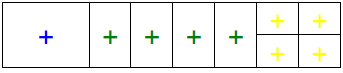
5) Use the tiles to create a length of x + 3. ( Draw below )

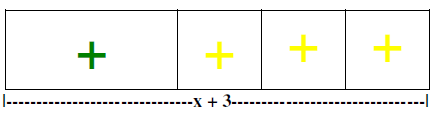
6) Keeping x + 3 as the length, try to create a rectangle that uses all the tiles from step
1. (Draw below) Explain whether or not all tiles can be used and why or why not.

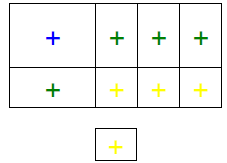
X + 3 does not divide evenly into x² + 4x + 4.