Math 111 Readiness Self Test

You do NOT have to turn this self assessment in to me. This self assessment is a tool to help you to pinpoint any weaknesses you might have as you enter this course.
You can check your answers with the Solutions to the Self Assessment when you are done.

My experience with a graphing calculator can best be described as:
• I used one often in the last math class I took. (Good!)
• I used one occasionally in the last math class I took. (Okay)
• I have used one just a few times . (You may need to do extra work to get your calculator skills up to speed)
• I have never used one before. (You will DEFINITELY need to do extra work to get your calculator skills up to speed!)

Work each problem. Check the appropriate box to the right of each problem.

1. Solve : 8(2x – 3) = 6x – 9	•This is too hard. I have never seen a problem like it before. •I have seen problems like this, but I don’t remember how to do it. •This problem is easy for me.
2. Solve by graphing : (by hand or using calculator) y = ⅔x + 3 y + 1 = 2x	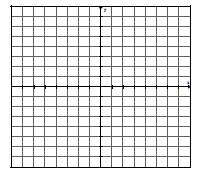•This is too hard. I have never seen a problem like it before. •I have seen problems like this, but I don’t remember how to do it. •This problem is easy for me.
3. Simplify the following expressions. a) -3a(a + 6b) + 5a(4b + 8) b) (2x + 8)(x – 3)	•This is too hard. I have never seen a problem like it before. •I have seen problems like this, but I don’t remember how to do it. •This problem is easy for me.
4. Solve: (use any method but indicate method used) x² + 11x + 18 = 0	•This is too hard. I have never seen a problem like it before. •I have seen problems like this, but I don’t remember how to do it. •This problem is easy for me.
5. Given y = f(x) = 2x² - 6x - 20 a) Find the vertex . b) Find the intercepts (x and y). c) Sketch graph.	•This is too hard. I have never seen a problem like it before. •I have seen problems like this, but I don’t remember how to do it. •This problem is easy for me.
6. Sketch: a) the graph of a quadratic equation when the leading coefficient is less than 0. b) the graph of any function that is NOT linear and is always increasing. c) any graph that is NOT a function. d) the graph of a quadratic equation that has imaginary roots .	•This is too hard. I have never seen a problem like it before. •I have seen problems like this, but I don’t remember how to do it. •This problem is easy for me.
7. If f(x) = 2x² + 4, find the following.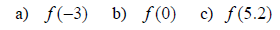	•This is too hard. I have never seen a problem like it before. •I have seen problems like this, but I don’t remember how to do it. •This problem is easy for me.
8. Solve the following equations by algebra (not graphing).	•This is too hard. I have never seen a problem like it before. •I have seen problems like this, but I don’t remember how to do it. •This problem is easy for me.
9. Simplify the following leaving no negative exponents.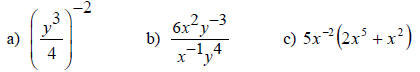	•This is too hard. I have never seen a problem like it before. •I have seen problems like this, but I don’t remember how to do it. •This problem is easy for me.