Math 135 Homework

Directions: Answer all the following questions. Be sure you have read and thought about the material
in Chapter 1 in our text. Try to phrase your answers in complete sentences so the reader has a narrative
instead of just short, clipped phrases or only symbolic notation . This is a group homework set so you will
need to work with your group members to create solutions and write them up nicely for presentation. Your
group'S written solutions are due Monday in class.

1) Give a definition for rational number . Using your definition, prove that the sum , difference, product, and
quotient (with one exceptional case) of rational numbers are again rational numbers. This is showing the
set of rational numbers is closed under these operations (again with one exception in the case of division).

2) Consider these predicate symbols with the indicated interpretations:
Rat(x) means `x is a rational number'.
Real(x) means `x is a real number '.
L(x; y) means `x is (strictly) less than y'.

a) Using these predicates, our two quantifier symbols, variables, and logical connectives, translate this
statement (*) into our formal symbolism:
(*) On the real number line , between any two rational numbers there is another rational number.
Informally speaking, this is saying the rational numbers are dense in themselves.

b) Prove statement (*) using an appropriate proof method .
Consider this statement:
(**) On the real number line , between any two real numbers there is a rational number.

c) Is (**) true or false? If false, produce a counterexample; if true outline a proof strategy on how you might
prove it. What type of proof would you use, what context or basic assumptions would be useful, etc?

3) Prove by contradiction that 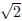is not rational. Note: this problem is NOT directly connected to the
previous ones but certainly should use your definition of a rational number.

4) Rework this problem from a previous problem set:
a) Write out in our style of mathematical language the standard 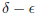definition of the following important
definition from calculus. Be sure to make all the quantifiers and logical connectives explicit so we can see
the full logical structure of this statement.

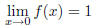
Here we assume f is some specific function. Be sure you have no free variables or mixed predicates and
quantifiers in your statement.
b) Now, form the negation of this statement and write it out in as positive a form as you can.
c) Write up an explanation of how to use your negated statement to show the following statement is false:

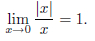
Notice that your statement in a) is universally quantified, so its negation is existential. How do we show an
existential statement is true?