Quadratic Functions and Models
Basic Forms of a Quadratic Function
There are two basic forms for quadratic functions. The first one (standard form)
is f (x) = ax2 + bx + c
and the second one ( vertex form ) is f (x) = a(x - h) 2 + k . The graph of a
quadratic function is a
parabola . If a is positive , the parabola opens upward and if a is negative, it
opens downward.
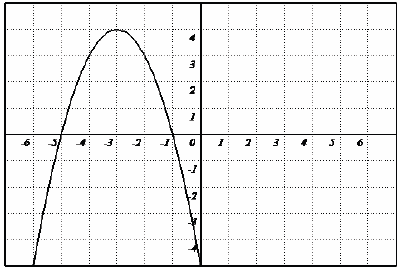
Example: Consider the following quadratic function . Find
the maximum or minimum function value ,
the axis of symmetry, and the range:
Finding the Vertex
Given the vertex form of a quadratic function, the vertex is the point (h, k ) .
Given the standard form of a
quadratic function , the x coordinate of the vertex is given by
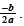
Example: Find the vertex .
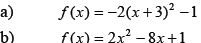
Additional Notes
• In exercises # 103 & 105, you are asked to use least -squares
regression to find a quadratic function that
models the data. This is done almost in exactly the same way that linear
regression is done.
| Prev | Next |