MATH 145 SAMPLE PROBLEMS FOR EXAM 2
Problems
(1) Let an denote the number of strings of n digits from
{0, 1, 2}, containing no consecutive 1s or 2s. Find
a1, a2, a3. Derive a second order homogeneous linear recurrence for an.
(2) Let dn be the derangement sequence. Using the
asymptotic fact that 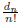 converges rapidly to
1/e , find
converges rapidly to
1/e , find
a good approximation to the probability that a random shuffling of a 52-card
deck will leave at most two
cards in their original position.
(3) Use bubble sort to arrange the list of numbers 7,4,6,3
in increasing order. List all the intermediate stages
of this process.
(4) In determining the generating function for the Catalan
numbers, we came up with the quadratic equation
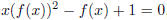 , where f(x) is regarded as the unknown . The
quadratic formula then gave us
, where f(x) is regarded as the unknown . The
quadratic formula then gave us
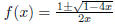 , an ambiguous result. Explain how to make
the correct choice for f(x).
, an ambiguous result. Explain how to make
the correct choice for f(x).
(5) Show that if you remove any edge from a tree with at least two vertices, you create a disconnected graph.
(6) A certain graph G has n red vertices, n white
vertices, and n blue vertices. What is the maximum
number of edges it can have if no edge has both of its end vertices the same
color?
(7) A spanning tree T for a graph G is a tour if each
vertex of the tree has degree ≤ 2. Give an example of
a graph with no tour. Show that Kn has a tour.
(8) What is the total number of simple graphs you can make
with three vertices? How about 4 vertices? Is
there a way of counting the number of graphs on n + 1 vertices, once you know
the number for n vertices?
9 Let 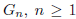 , be the simple
graph with vertices
, be the simple
graph with vertices 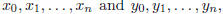 where the edges are
where the edges are
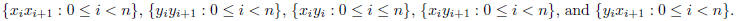
Is  bipartite? How about planar?
bipartite? How about planar?
(1) Let an denote the number of strings of n digits from
{0, 1, 2}, containing no consecutive 1s or 2s. Find
a1, a2, a3. Derive a second order homogeneous linear recurrence for an.
a1 = 3, a2 = 7, a3 = 17. Call a string good if it contains
no consecutive 1s or 2s. Each
string of length n + 1 is formed by adding a digit to the end of a string of
length n. Let
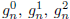 be the number of good strings of length n
that end in 0, 1, 2, respectively. Then
be the number of good strings of length n
that end in 0, 1, 2, respectively. Then
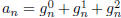 Now it is clear that
Now it is clear that
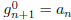 ; goodness is neither ruined nor created by
; goodness is neither ruined nor created by
affixing a 0. The only way to create a good (n + 1)-length string ending in a 1
is for the n-
string you affix the 1 to to be good and to end in either 0 or 2. This tells us
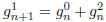
Likewise, 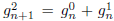 . Clearly, by symmetry (switch 1s
and 2s in any given string),
. Clearly, by symmetry (switch 1s
and 2s in any given string),
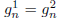 . Let this number be
. Let this number be
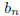 . Then
. Then 
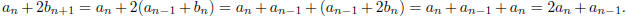
This gives us the initial value recurrence , 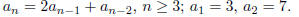
(2) Let dn be the derangement sequence. Using the
asymptotic fact that 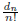 converges rapidly to
1/e , find
converges rapidly to
1/e , find
a good approximation to the probability that a random shuffling of a 52-card
deck will leave at most two
cards in their original position.
The probability P is exactly
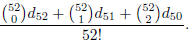
To get the desired approximation, we replace each
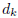 by
by 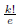 ,
obtaining
,
obtaining 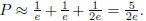
(3) Use bubble sort to arrange the list of numbers 7,4,6,3
in increasing order. List all the intermediate stages
of this process.
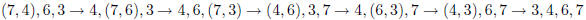
(4) In determining the generating function for the Catalan
numbers, we came up with the quadratic equation
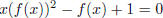 , where f(x) is regarded as the unknown.
The quadratic formula then gave us
, where f(x) is regarded as the unknown.
The quadratic formula then gave us
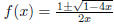 , an ambiguous result. Explain how to make
the correct choice for f(x).
, an ambiguous result. Explain how to make
the correct choice for f(x).
Let 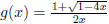 . Then, as x -> 0,
the denominator converges to 0, while the numerator
. Then, as x -> 0,
the denominator converges to 0, while the numerator
converges to 2. Then 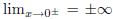 . Since every power
series in x is defined at x = 0,
. Since every power
series in x is defined at x = 0,
g cannot be the generating function for  . The
other possibility is
. The
other possibility is 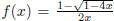 . As
. As
x -> 0, both numerator and denominator converge to 0; so we may use
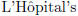 rule to
rule to
obtain 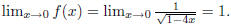
(5) Show that if you remove any edge from a tree with at least two vertices , you create a disconnected graph.
Suppose T be the tree in question; say T has p≥2 vertices.
Then the number of edges is
p − 1. Let the resulting graph be G. Then it has p vertices and p − 2 edges, so
cannot be a
tree. However, since removal of edges does not create cycles, G can have no
cycles; hence, if
it were connected, it would have to be a tree. We conclude that G cannot be
connected.
(6) A certain graph G has n red vertices, n white
vertices, and n blue vertices. What is the maximum
number of edges it can have if no edge has both of its end vertices the same
color?
Let the vertex set V be the disjoint union
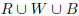 , where |R| = |W| = |B| = n. Then
, where |R| = |W| = |B| = n. Then
there are n^2 possible edges between vertices in R and vertices in W; likewise
for R and B ;
likewise for W and B. No two edge sets have any edges in common ; so the total
possible
number of edges is 3n^2.
(7) A spanning tree T for a graph G is a tour if each
vertex of the tree has degree ≤ 2. Give an example of
a graph with no tour. Show that 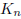 has a tour.
has a tour.
The triod 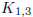 has no tour.
In fact, any tree with a vertex of degree ≥ 3 has no tour. As for
has no tour.
In fact, any tree with a vertex of degree ≥ 3 has no tour. As for
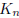 , list its vertices as
, list its vertices as
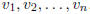 . Then there is a unique edge from
. Then there is a unique edge from
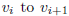 for each
for each
1 ≤ i < n, and this path gives us a tour.
(8) What is the total number of simple graphs you can make
with three vertices? How about 4 vertices? Is
there a way of counting the number of graphs on n + 1 vertices, once you know
the number for n vertices?
Let 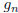 be the number of
simple graphs on the vertices
be the number of
simple graphs on the vertices 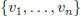 . Then
. Then
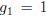 ; since
; since
there are no loops, there is just one vertex and no edges. With two vertices,
they’re either
adjacent or they aren’t; so 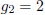 . For three
vertices, you have either no edges (1 way), one
. For three
vertices, you have either no edges (1 way), one
edge (3 ways), two edges (3 ways), or three edges (1 way). Hence
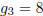 . Suppose we want
. Suppose we want
to count the number of simple graphs on vertex set
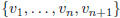 . We may specify any
. We may specify any
such graph by determining the adjacency structure on vertices
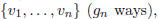 and
and
then pick a set of vertices from 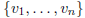 to form an
edge with
to form an
edge with 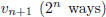 . Thus
. Thus
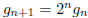 . ( Solving this recurrence gives us
. ( Solving this recurrence gives us
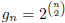 . Another way to get this result is
. Another way to get this result is
to line up the pairs of vertices (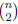 ways) and
to decide which of these pairs are to receive
ways) and
to decide which of these pairs are to receive
an edge (2 ways for each). This also gives us  .)
.)
9 Let 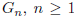 , be the simple
graph with vertices
, be the simple
graph with vertices 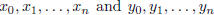 , where the edges are
, where the edges are
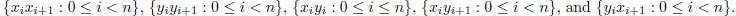
Is 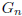 bipartite? How about planar?
bipartite? How about planar?
The graph is not bipartite because it has a cycle
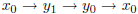 of odd length 3. It is
of odd length 3. It is
planar because it contains no subdivision of 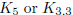 .
(This latter fact may be determined
.
(This latter fact may be determined
by induction.)
| Prev | Next |