Strategy for solving Linear Equations with one variable
Section 9.1 – 9.3 Worksheet
Strategy for solving Linear Equations with one variable:
1. Simplify both sides of the equation
§ Clear Parentheses (Use distributive property as needed )
§ Clear fractions or decimals by multiplying both sides by a common denominator
(for fractions) or a power of 10 (for decimals)
§ Combine like terms on each side of equation
2. Use addition property of equality to get all variable terms on one side and
constants on the
other (Keep using this property as many times as needed ).
3. Use multiplication property to make the coefficient of the variable = one
4. Check your solution in original equation
Remember:
Get rid of fractions and decimals by multiplying by LCD or power of 10
Distribute your negatives
Change subtraction to addition to make it easier
Don’t try to do too many steps at one time
| Example: | Description of steps: |
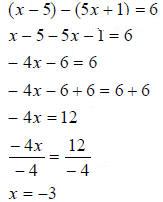 |
Step 1: Distribute (notice I distributed the
negative) Step 1c. Combine like terms . Step 2: Addition property of equality to get x-term by itself Step 3: Multiplication property of equality to get x by itself |
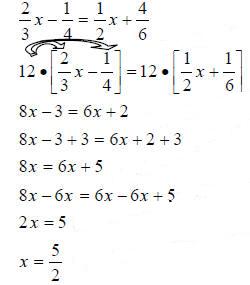 |
Step 1a: Get rid of fractions by multiplying both
sides by the LCD (12 is the LCD) Step 2: Addition property of equality to get x-term on one side and constants on the other. Step 3: Multiplication property of equality to get x by itself. Solution: Fractions are perfectly acceptable answers! |
Solve the following equations:
| Equation: | Solution: |
| 4x - 9 = -25 | |
| 4x + 3 = 2x - 5 | |
| 15x - 7 - 3x +12 = 4x - 2 + 6x | |
| x - 9x + 20 = -3x -5 | |
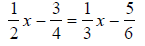 |
|
| 3( x - 1) = 2x + 6 | |
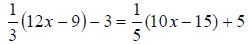 |
|
| - (4x - 5) = 2(5x -1) - 7 | |
| 0.2x - (0.3x - 0.5) = -1.3 | |
| 6( x - 5) - (3x + 2) = -5x + 8 |
| Prev | Next |