Math 41 Study Guide
6.3 Trigonometric Functions of Angles
• Memorize in which quadrants each trig function is positive
• Reference angles: Acute angle formed by x-axis and terminal side
• Using reference angles to evaluate trig functions
• Reciprocal Identities :
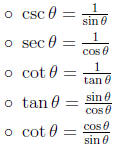
• Pythagorean Identities:
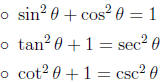
• Expressing trig functions in terms of other trig
functions
• Evaluating trig functions using identities
• Area of a Triangle: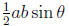 
(where θ is the
angle between a and b)
6.4 Law of Sines
• Law of Sines: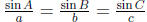 
• Solving triangles :
o SAA
o SSA (either no solution, one solution or two solutions )
6.5 Law of Cosines
• Law of Cosines:
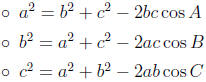
Solving triangles:
o SSS
o SAS
• Navigation: Bearing
• Heron’s Formula: Area of a triangle is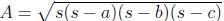 
where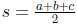 
7.1 The Unit Circle
• Terminal Points
• Reference Numbers
7.2 Trigonometric Functions of Real Numbers
• Definitions of trig functions using unit circle
• Domains of trig functions
• Reciprocal Identities (see 6.3)
• Pythagorean Identities (see 6.3)
• Even-Odd Properties:
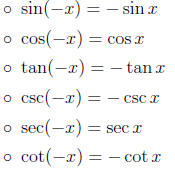
7.3 Trigonometric Graphs
• Periodic Properties:
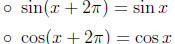
• Graphs of sin and cos
• Transformations
• y = a sin k(x − b) has amplitude |a|, period
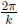, and phase shift b
• y = a cos k(x − b) has amplitude |a|, period
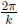, and phase shift b
7.4 More Trigonometric Graphs
• Periodic Properties:
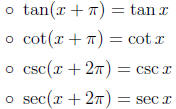
• Graphs of tan, cot, csc, sec
• Transformations
8.1 Trigonometric Identities
• Cofunction Identities:
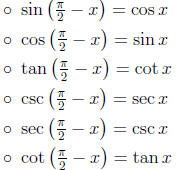
• Simplifying trig expressions
• Proving trig identities
8.2 Addition and Subtraction Formulas
• Addition Formulas:
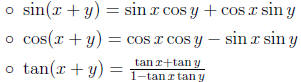
• Subtraction Formulas:
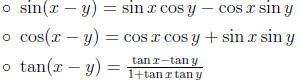
• Sums of Sines and Cosines: change Asin x + B cos x to k
sin(x +Ø )
o First calculate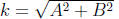 
o Ø satisfies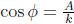 
and
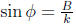
8.3 Double-Angle, Half-Angle, and Product-Sum Formulas
• Double-Angle Formulas:
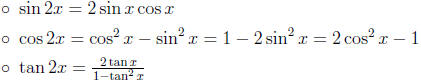
• Half-Angle Formulas:
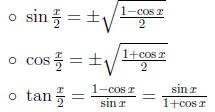
• Formulas for lowering powers:
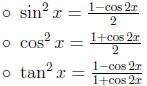
• Product-to-Sum Formulas:
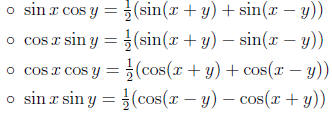
• Sum-to-Product Formulas:
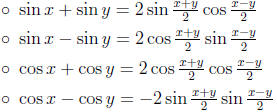
8.4 Inverse Trigonometric Functions
• Grahps of sin-1, cos-1, tan-1
• Domains and Ranges of inverse trig functions
• Evaluating expressions involving inverse trig functions
8.5 Trigonometric Equations
• Methods to solve trig equations:
o Factoring
o Substitution
o Using trig identities
o Squaring (check answers!)
9.1 Polar Coordinates
• Definition of polar coordinates
• Relationship between polar and rectangular coordinates:
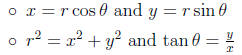
• Converting equations between polar and rectangular coordinates
9.2 Graphs of Polar Equations
• Use table to graph
• Symmetry:
o x-axis (polar axis): equation unchanged when θ replaced by −θ
o origin (pole): equation unchanged when r replaced by −r
o y-axis: equation unchanged when θ replaced by π −θ
9.3 Polar Form of Complex Numbers; DeMoivre’s Theorem
• Polar Form of Complex Numbers:
z = r(cosθ + i sinθ ) where r is the modulus and θ is the
argument
• Conversion between standard and polar form:
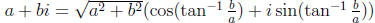
• Multiplication of complex numbers in polar form: multiply moduli, add
arguments
• Division of complex numbers in polar form: divide moduli, subtract arguments
• DeMoivre’s Theorem: if z = r(cosθ + i sinθ ) then zn = rn(cos(nθ
) + i sin(nθ ))
• n-th roots: if z = r(cosθ + i sinθ ) then z has n n-th roots and
they are:
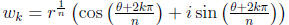for k = 0, 1, 2, . . . , n − 1
12.1 Sequences and Summation Notation
• A few commonly used terms:
o (−1)n or (−1)n+1 for sequences alternating in sign
o 2n for even numbers
o 2n − 1 for odd numbers
• Recursively defined sequences, Fibonacci Numbers
• Partial sums
• Sigma notation: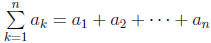 
• Properties:
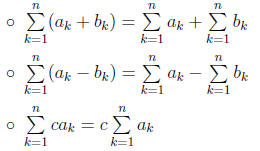
12.2 Arithmetic Sequences
• Arithmetic sequence: a, a + d, a + 2d, . . .
• 
= a + d(n − 1)
• Gauss: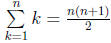 
• Partial sums of an arithmetic sequence: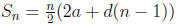 
12.3 Geometric Sequences
• Geometric sequence: a, ar, ar2, . . .
• 
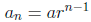
• Partial sums of an arithmetic sequence: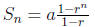 
• Sum of an infinite geometric series: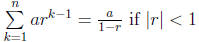 
| Prev | Next |