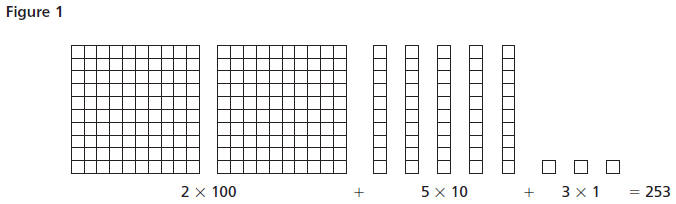
Math Glossary

base ten number system The common number
system we use . Our number system is based on the
number 10 because we have ten fingers with which to
group. Each group represents ten of the previous
group, so we can write numbers efficiently. By
extending the place value system to include places
that represent fractions with 10 or powers of 10 in
the denominator, we can easily represent very large
and very small quantities. Below is a graphic
representation of counting in the base ten number
system. (Figure 1)

benchmark A reference number that can be used to
estimate the size of other numbers. For work with
fractions, 0, 1/2, and 1 are good benchmarks. We often
estimate fractions or decimals with benchmarks
because it is easier to do arithmetic with them , and
estimates often give enough accuracy for the
situation. For example, many fractions and
decimals—such as 37/50, 5/8, 0.43, and 0.55—can be
thought of as being close to 1/2.You might say 5/8 is
between 1/2 and 1 but closer to 1/2, so you can estimate 5/8
to be about 1/2 .We also use benchmarks to help
compare fractions and decimals. For example, we
could say that 5/8 is greater than 0.43 because 5/8 is
greater than 1/2 and 0.43 is less than 1/2 .


decimal A special form of a fraction. Decimals, or
decimal fractions, are based on the base ten
place-value system. To write numbers as decimals, we
use only 10 and powers of 10 as denominators .
Writing fractions in this way saves us from writing
the denominators because they are understood. When
we write as a decimal (0.375) the denominator
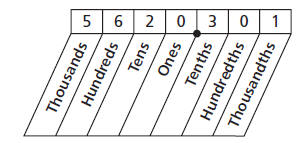
of 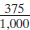is understood. The digits to the left of the
decimal point show whole units. The digits to the
right of the decimal point show a portion of a whole
unit. The diagram shows the place value for each
digit of the number 5,620.301.

denominator The number written below the line in
a fraction. In the fraction 3/4, 4 is the denominator. In
the part-whole interpretation of fractions, the
denominator shows the number of equal-size parts
into which the whole has been split.

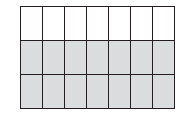
equivalent fractions Fractions that are equal in
value, but may have different numerators and
denominators . For example, 2/3 and 14/21 are equivalent
fractions. The shaded part of this rectangle represents
both 2/3 and 14/21.

fraction A number (quantity) of the form a/b where a
and b are whole numbers. A fraction can indicate a
part of a whole object, set, or measurement unit; a
ratio of two quantities ; or a division. For the picture
below, the fraction 3/4 shows the part of the rectangle
that is shaded. The denominator 4 indicates the
number of equal-size pieces. The numerator 3
indicates the number of pieces that are shaded.

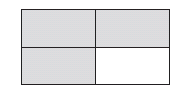
The fraction 3/4 could also represent three of a group
of four items meeting a particular criteria. For
example, when 12 students enjoyed a particular
activity and 16 students did not, the ratio is 3 to 4.
Another example is the amount of pizza each person
receives when three pizzas are shared equally among
four people (3 ÷ 4 or 3/4 of a pizza per person).

improper fraction A fraction in which the
numerator is larger than the denominator. An
improper fraction is a fraction that is greater than 1.
The fraction 5/2 is an improper fraction. The fraction 5/2
means 5 halves and is equivalent to 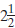, which is
greater than 1.

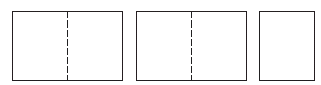
mixed number A number that is written with both
a whole number and a fraction. A mixed number is
the sum of the whole number and the fraction. The
number 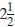represents two wholes and one half and
can be thought of as 2 + 1/2.

numerator The number written above the line in a
fraction. In the fraction 5/8, 5 is the numerator. When
you interpret the fraction 5/8 as a part of a whole, the
numerator 5 represents 5 of 8 equal parts.

percent “Out of 100.”A percent is a special decimal
fraction in which the denominator is 100.When we
write 68%, we mean 68 out of 100, 68/100, or 0.68.We
write the percent sign (%) after a number to indicate
percent. The shaded part of this square is 68%.

ratio A number, often expressed as a fraction, used
to make comparisons between two quanitities. Ratios
may also be expressed as equivalent decimals or
percents. 3/5, 0.6, and 60% are all ratios. A phrase such
as “120 out of 200” is another way to represent a ratio.

rational number A number that can be written as a
quotient of two positive or negative whole numbers.
You are familiar with positive rational numbers like
3/4, 107/5,and 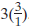. Some examples of the negative
rational numbers you will see in the future are –3,
–2/5, and –20. Both positive and negative rational numbers
can be used to represent real -life situations. For
example, temperatures or yardage during a football
game can be positive, negative, or 0.There are other
numbers, such as pi, that are not rational numbers.

unit fraction A fraction with a numerator of 1. In
the unit fraction 1/13, the denominator 13 indicates
the number of equal-size parts into which the whole
has been split. The fraction represents the quantity of
1 of those parts.