Systems of Linear Equations
Introduction: One equation in one variable
3x + 2 = 14
3x + 2 − 2 = 14 − 2
3x = 12
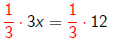
x = 4
we:
• Subtract two from each side to have the variable on one side
and the constant on the other
• Divide both sides by 3 to scale the coefficient of x to be one .
• See the solution x = 4
Alegebra (al-jabr) = “Restoration”
= “Do the same thing to both sides of the equation”
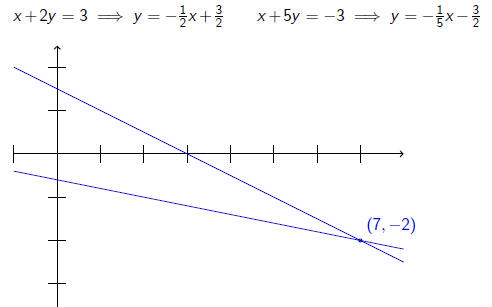
Systems of two equations in two variables
x + 2y = 3
x + 5y = −3
We might
• Subtract both equations to get −3y = 6
• Divide by −3 to get y = −2
• Substitute back into the first equation to get
x + 2(−2) = 3 -> x = 7
So the solution is the pair (7,−2).
Geometric interpretation
Each equation represents a line in the plane
Anamolies
Two lines need not intersect in a point!
• They may be parallel
• They may be coincidental
Systems of three equations in three variables
Solve
x − 2y + z = 0
2y − 8z = 8
−4x + 5y + 9z = −9
Solution
x = 29, y = 16, z = 3
Geometric Interpretations
• In three variables , the solution set to one equation is
a plane
• Multiple equations give intersections of these planes.
• How can planes intersect?
• not at all
• lines
• a point
| Prev | Next |