DEFINING LEARNER OUTCOMES FOR INTERMEDIATE ALGEBRA
The following learner outcomes for Intermediate Algebra
are classified into 3
categories.
 These core outcomes represent the
fundamental concepts of
These core outcomes represent the
fundamental concepts of
Intermediate algebra which students should be able to do at the end of this
course. Some
of these concepts are new to the students while others have been introduced in
elementary algebra and now require greater depth.
 Students should have experience with these
outcomes in order to
Students should have experience with these
outcomes in order to
begin developing familiarity with the ideas and confidence performing related
skills.
Indicators for these outcomes would be on midterms but not necessarily on the
final
exam.
 These outcomes are optional. An instructor
may expect these of
These outcomes are optional. An instructor
may expect these of
students during the course but not in lieu of a C1 or C2 outcome.
Simplifying Expressions
C1  1.
1.  Factor
an algebraic expression using a combination of greatest common
Factor
an algebraic expression using a combination of greatest common
 factor, difference of two squares , sum or
difference of two cubes , and/or
factor, difference of two squares , sum or
difference of two cubes , and/or
 trinomial factoring
trinomial factoring
C1  2.
2.  Use
factoring procedures to solve equations and problems.
Use
factoring procedures to solve equations and problems.
C1  3.
3.  Know
and apply the rules of integral and fractional exponents.
Know
and apply the rules of integral and fractional exponents.
C2  4.
4.  Use
scientific notation in application problems.
Use
scientific notation in application problems.
O  5.
5.
 Divide polynomials using synthetic division.
Divide polynomials using synthetic division.
Complex Numbers
C1  1.
1.  Rewrite
a radical expression with a negative radicand in the a + bi form.
Rewrite
a radical expression with a negative radicand in the a + bi form.
C1  2.
2.  Combine
complex numbers by adding, subtracting , multiplying, or dividing
Combine
complex numbers by adding, subtracting , multiplying, or dividing
 (by bi only).
(by bi only).
C2  3.
3.  Use
conjugates to divide complex numbers.
Use
conjugates to divide complex numbers.
O  4.
4.
 Evaluate powers of i.
Evaluate powers of i.
Functions
C1  1.
1.  Evaluate
functions using numerical and algebraic values.
Evaluate
functions using numerical and algebraic values.
C1  2.
2.  Identify
domain (inputs) and range (outputs) graphically for basic functions.
Identify
domain (inputs) and range (outputs) graphically for basic functions.
C1  3.
3.  Interpret
functional notation in a variety of application problems.
Interpret
functional notation in a variety of application problems.
C2  4.
4.  Write
the equation of the inverse for linear, exponential, and logarithmic
Write
the equation of the inverse for linear, exponential, and logarithmic
 functions and show their relationship
graphically.
functions and show their relationship
graphically.
C2  5.
5.  Determine
if a relation is a function by looking at a graph, table, or equation.
Determine
if a relation is a function by looking at a graph, table, or equation.
C2  6.
6.  Combine
two functions by adding, subtracting, multiplying, dividing, and
Combine
two functions by adding, subtracting, multiplying, dividing, and
 composition.
composition.
O  7.
7.  Identify
which functions are one-to-one by looking at their graphs.
Identify
which functions are one-to-one by looking at their graphs.
Linear Functions , Equations, and Inequalities
C1  1.
1.  Write
the equation of a linear function if given two ordered pairs, two data
Write
the equation of a linear function if given two ordered pairs, two data
 points, or a linear graph. Use functional
notation in the answer.
points, or a linear graph. Use functional
notation in the answer.
C1  2,
2,  Solve
compound linear inequalities joined by and or or, and of the form
Solve
compound linear inequalities joined by and or or, and of the form
 C<ax + b <d. Express answer algebraically,
graphically, and using interval
C<ax + b <d. Express answer algebraically,
graphically, and using interval
 notation.
notation.
C1  3.
3.  Write
the equation of a linear function given the slope and a point on the l
Write
the equation of a linear function given the slope and a point on the l
 line.
line.
C1  4.
4.  Express
the slope as a rate of change using appropriate units.
Express
the slope as a rate of change using appropriate units.
C2  5.
5.  Solve
an equation or inequality involving absolute value of the form lax + bl .
Solve
an equation or inequality involving absolute value of the form lax + bl .
 Express answer in interval notation.
Express answer in interval notation.
C2  6.
6.  Graph
linear inequalities in two variables
Graph
linear inequalities in two variables
C2  7.
7.  Write
the equation of a linear function given a point and a line perpendicular
Write
the equation of a linear function given a point and a line perpendicular
 or parallel to it.
or parallel to it.
C2  8.
8.  Isolate
a particular variable in a literal equation.
Isolate
a particular variable in a literal equation.
Quadratic Functions
C1  1.
1.  Graph
a quadratic function by finding the vertex, x- and y-intercepts.
Graph
a quadratic function by finding the vertex, x- and y-intercepts.
C1  2.
2.  Use
quadratic formula to find exact values of a quadratic equation with
Use
quadratic formula to find exact values of a quadratic equation with
 irrational or imaginary solutions.
Approximate the irrational solutions.
irrational or imaginary solutions.
Approximate the irrational solutions.
C1  3.
3.  Given
a quadratic model, find and interpret the maximum or minimum
Given
a quadratic model, find and interpret the maximum or minimum
 values, and the intercepts.
values, and the intercepts.
C1  4.
4.  Solve
an application problem involving quadratic equations.
Solve
an application problem involving quadratic equations.
C2  5.
5.  Solve
a quadratic inequality. Write the answer in interval notation.
Solve
a quadratic inequality. Write the answer in interval notation.
O  6.
6.
 Relate the discriminant in the quadratic
formula to the graph of a parabola.
Relate the discriminant in the quadratic
formula to the graph of a parabola.
Rational Expressions and Equations
C1  1.
1.  Add,
subtract, multiply, divide rational expressions. Reduce the answers.
Add,
subtract, multiply, divide rational expressions. Reduce the answers.
C1  2.
2.  Simplify
a complex fraction.
Simplify
a complex fraction.
C1  3.
3.  Solve
a rational equation and check for extraneous solutions.
Solve
a rational equation and check for extraneous solutions.
C1  4.
4.  Solve
an application problem that involves rational expressions.
Solve
an application problem that involves rational expressions.
O  5.
5.
 Solve a rational inequality.
Solve a rational inequality.
Radical Equations and Expressions
C1  1.
1.  Solve
a radical equation that produces a second-degree equation. Check for
Solve
a radical equation that produces a second-degree equation. Check for
 extraneous solutions.
extraneous solutions.
C1  2.
2.  Know
the meaning of rational exponents and their relationship to radical
Know
the meaning of rational exponents and their relationship to radical
 form.
form.
C2  3.
3.  Simplify
radical expressions with emphasis on cube roots and higher .
Simplify
radical expressions with emphasis on cube roots and higher .
C2  4.
4.  Rewrite
radical expressions by rationalizing numerator or denominator.
Rewrite
radical expressions by rationalizing numerator or denominator.
C2  5.
5.  Add,
subtract, multiply, and divide radical expressions.
Add,
subtract, multiply, and divide radical expressions.
C2  6.
6.  Solve
application problems involving the Pythagorean Theorem.
Solve
application problems involving the Pythagorean Theorem.
O  7.
7.
 State the domain of radical functions.
State the domain of radical functions.
Exponential and Logarithmic Equations and Expressions
C1  1.
1.  Solve
basic exponential and logarithmic equations.
Solve
basic exponential and logarithmic equations.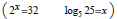
C1  2.
2.  Evaluate
basic logarithmic expressions, and convert between logarithmic and
Evaluate
basic logarithmic expressions, and convert between logarithmic and
 exponential form.
exponential form.
C1  3.
3.  Solve
an exponential equation that requires the use of logarithms.
Solve
an exponential equation that requires the use of logarithms.
C1  4.
4.  Solve
a logarithmic equation requiring properties of logarithms to condense.
Solve
a logarithmic equation requiring properties of logarithms to condense.
 Be able to use base
Be able to use base
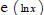 or base
or base 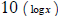 logarithms.
logarithms.
C1  5.
5.  Solve
for specific values of the independent or dependent variables in
Solve
for specific values of the independent or dependent variables in
 exponential and logarithmic expressions.
exponential and logarithmic expressions.
C2  6.
6.  Graph
a basic exponential or logarithmic function.
Graph
a basic exponential or logarithmic function.
C2  7.
7.  Know
the graphical relationship between exponential and logarithmic
Know
the graphical relationship between exponential and logarithmic
 functions.
functions.
C2  8.
8.  Solve
an application problem involving a given exponential or logarithmic
Solve
an application problem involving a given exponential or logarithmic
 model.
model.
O  9.
9.
 Change the base of logarithmic expressions to
other bases.
Change the base of logarithmic expressions to
other bases.
O  10.
10.
 Find a model for natural growth and decay
problems.
Find a model for natural growth and decay
problems.
System of Equations
C1  1.
1.  Solve
linear and nonlinear systems of equations algebraically and graphically.
Solve
linear and nonlinear systems of equations algebraically and graphically.
O  2.
2.
 Solve an application problem in two
variables.
Solve an application problem in two
variables.
Conic Sections
C1  1.
1.  Graph
the equation of a circle by plotting the center and using the radius.
Graph
the equation of a circle by plotting the center and using the radius.
C1  2.
2.  Graph
the parabola given by f (x) = ax2 + bx + c or x = ay2 + by + c by finding the
Graph
the parabola given by f (x) = ax2 + bx + c or x = ay2 + by + c by finding the
 vertex and another point.
vertex and another point.
C2  3.
3.  Identify
the graph of a second-degree equation. (no xy term )
Identify
the graph of a second-degree equation. (no xy term )
C2  4.
4.  Find
the distance between two points.
Find
the distance between two points.
C2  5.
5.  Find
the midpoint between two points.
Find
the midpoint between two points.
O  6.
6.
 Graph the equation of an ellipse or a
hyperbola .
Graph the equation of an ellipse or a
hyperbola .
| Prev | Next |