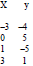Math Grade 8 Standards

Idaho Department of Education Content Standards	Objective	Sub Objectives	Task Analysis	Essential Vocabulary	Sample Assessment	Resources
Standard 3: Concepts and Language of Algebra and Functions
Goal 3.1: Use algebraic symbolism as a tool to represent mathematical relationships .	8.M.3.1.1 Use variables in expressions, equations, and inequalities. CL: D Calc: CN Content Limit: Evaluate an expression by substituting a number for every variable in the expression. Items are limited to at most three variables at a time. Items may also check solutions to equations or inequalities by substituting values for the variable(s) in an equation or inequality.	• Use variables in expressions, equations, and inequalities	• Apply order of operations to variable expressions • Evaluate expressions by replacing variables with given numbers	variable • algebraic • expression • evaluate • simplify	• Evaluate for n=3: 2n+5-n • Evaluate the expression for m=5.2 and n=4.1: 5m-2n*3
	8.M.3.1.2 Translate simple word statements and story problems into algebraic expressions and equations. CL: D Calc: CN Content Limit: Items should be set in a real-world context. Expressions and equations may contain at most three operations and may require at most two grouping symbols . May contain one or two variables.	• Translate simple word statements and story problems into algebraic expressions and equations	• Assign variables to write algebraic expressions • Represent given mathematical vocabulary with appropriate operational symbols	sum • difference • quotient • product • less/greater than • increased/decreased by	• An object's weight on Mars is 0.38 times the object 's weight on Earth. Write an algebraic expression for an object's weight on Mars.
	8.M.3.1.3 Use symbols “<,” “>,”“=,” “≤,” “≥.” and “≠” to express relationships. CL: D Calc: CN Content Limit: Items should be set in a real-world context. Item may include integers between −50 and 50, up to three operations, at most two grouping symbol, and exponents limited to 2, 3, and 4. May include one variable.	• Use symbols “<,” “>,”“=,” “≤,” “≥,” and “≠” to express relationships	• Define symbols of inequality • Write inequalities and equations to represent numerical relationships	not equal	• Write the inequality for:y minus 4 is a negative number. People at least 65 years old receive a senior citizen discount.
Goal 3.2: Evaluate algebraic expressions.	8.M.3.2.1 Use and apply the following properties in evaluating algebraic expressions: commutative, associative, identity, zero, inverse, distributive, and substitution. CL: C Calc: CN Content Limit: Items can use positive fractions with no more than two-digit numerators and denominators or decimals less than ten-thousandths. Expressions may include integers between −50 and 50, up to three operations, at most two grouping symbol, and exponents limited to 2, 3, and 4. May include one variable.	• Use and apply the following properties in evaluating algebraic expressions: commutative, associative, identity, zero, inverse, distributive, and substitution	• Use associative and commutative properties to simplify expressions • Identify identity properties of addition and multiplication • Identify inverse properties of addition and multiplication • Apply distributive property to expressions • Describe zero property • Practice evaluating expressions using substitution	commutative • associative • identity • zero • inverse • distributive • substitution	• Use the appropriate property to simplify: 2.5+5.3+7.5 (n+14)(-8) -2135
	8.M.3.2.2 Use the order of operations in evaluating simple algebraic expressions. CL: C Calc: CN Content Limit: Expressions may include parentheses, exponents, multiplication, division, addition, and/or subtraction. Items can use positive fractions with no more than two-digit numerators and denominators or decimals less than ten-thousandths. Roots are limited to square roots and cube roots. Items require students to compute only the cube root of 8, 27, 64, 125, or 1,000. May include one or two variables.	• Use the order of operations in evaluating simple algebraic expressions	• Recognize and apply correct order of operations		• Evaluate: n+(13-n)/5 for n=3
	8.M.3.2.3 Simplify algebraic expressions. CL: C Calc: CN Content Limit: Items can use positive fractions with no more than two-digit numerators and denominators or decimals less than ten-thousandths. Expressions may include integers between −50 and 50, up to three operations, at most two grouping symbol, and exponents limited to 2, 3, and 4. May include one or two variables.	• Simplify algebraic expressions	• Apply properties from 8.M.3.2.1 • Illustrate simplifying expressions by combining like terms and using distributive property	like terms	• Simplify: 8c-3(c+5)
Goal 3.3: Solve algebraic equations and inequalities.	8.M.3.3.1 Solve one- and two- step equations and inequalities. CL: C Calc: YES Content Limit: Items can use positive fractions with no more than one-digit numerators and denominators or decimals less than ten-thousandths. Equations and inequalities may include integers between −50 and 50. Variable may appear on left or right side of equal or inequality sign.	• Solve one- and two-step equations and inequalities	• Apply properties from 8.M.3.2.1 • Apply addition and subtraction properties of equality/inequality • Apply multiplication and division properties of equality/inequality including multiplicative inverse/reciprocal	isolate • solution • reciprocal/multiplicative • inverse	• 7+x/4=3 • 7b+3=24
	8.M.3.3.2 Match graphical representations with simple linear equations . CL: C, D Calc: CN Content Limit: The x- and y-axes may have different scales . Linear equations will be given in slope-intercept (y = mx + b) form.	• Recognize linear equations in slope-intercept form • Match graphical representations with simple linear equations	• Identify parts of a coordinate plane • Create a table of values given a linear equation and use the ordered pairs to plot a line • Identify slope and y-intercept from y = mx + b and represent as a graph	origin • x- and y-axes • ordered pair • slope • y-intercept • linear • slope intercept form • coordinate plane	• Which of the following is a graph of the equation y=2x-1? • Graph y=-2/3x-2 using 0,3 and 6 as the x values
Goal 3.4: Understand the concept of functions.	8.M.3.4.1 Extend patterns and identify a rule (function) that generates the pattern using rational numbers . CL: E Calc: YES Content Limit: Items may require a verbal description of the pattern. Variables can be used to write the rule (function). Items should not include more that two variables or include more than two operations. Fraction denominators limited to 2, 3, 4, 5, 6, 8, and 10. Decimals limited to tenths, hundredths, and thousandths. Functions must be expressible as y = mx + b. Items may ask the student to extend the pattern, state the rule for the pattern, or both.	• Extend patterns and identify a rule (function) that generates the pattern using rational numbers	• Recognize input/output relationships of functions • Represent function using a table • Write a rule to extend pattern • Use function notation to represent relationship (y = mx + b as f(x) = mx + b)	function • function rule • input/output • relation	• Graph the relation in the table. Then use the vertical-line test. Is the relation a function? • Identify the slope and y-intercept of the graph of the equation. Then graph the equation. y = x + 1
	8.M.3.4.2 Use relationships to explain how a change in one quantity may result in a change in another, and identify the relationship as a positive, negative, or neither. CL: Calc: Content Limit: Assessed in the classroom, not on the ISAT.	• Use relationships to explain how a change in one quantity may result in a change in another, and identify the relationship as a positive, negative, or neither	• Use a graph or table to show how a change in one quantity affects the other quantity	quantity • rate of change
	8.M.3.4.3 Use appropriate vocabulary and notations. CL: Calc: Content Limit: Assessed in the classroom, not on the ISAT.	• Use appropriate vocabulary and notations	• Communicate using correct mathematical terminology
Goal 3.5: Represent equations, inequalities and functions in a variety of formats.	8.M.3.5.1 Represent a set of data in a table, as a graph, and as a mathematical relationship. CL: C, D Calc: CN Content Limit: On the graph, x- and y-axes may have different scales. Items do not require students to graph or generate a table of a non-linear relation; students may read points off of a graph of a non-linear relation. Items may include real-world context. Given a continuous (i.e., individual points not indicated) linear graph, students will generate a table of values. Relationship is presented as a table, graph, or equation. The answer options will include a table, a graph, or an equation.	• Represent a set of data in a table as a graph, and as an equation	• Establish input/output relationship between data in table and graph or equation	data table	• Write a rule for the linear function in the graph. • The scatter plot shows the study times and test scores for a number of students. • Describe the person represented by point A.
Goal 3.6: Apply functions to a variety of problems.	8.M.3.6.1 Use patterns and linear functions to represent and solve problems. CL: D Calc: YES Content Limit: Patterns may include rational numbers. Linear functions are limited to whole number variable values.	• Use patterns and linear functions to represent and solve problems	• Identify patterns in problems • Discover function rule for pattern • Evaluate using function