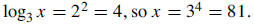MATHEMATICS CONTEST 2006 SOLUTIONS
PART II: 30 Minutes; CALCULATORS NEEDED
Section A. Each correct answer is worth 1 point.
| 1. Evaluate: 45 − 54
Solution : This is simple on a calculator, but even without one, we can compute
45 = 42 · 42 · 4 = |
| 2. The area of a triangle is 2006 sq. cm. Its base is 2006 cm. What is its
height? Solution: Area equals 1/2bh = 1/2(2006)(h) = 2006, so h = 2 cm. |
| 3. If 2/5
of a number is 2.5, what is the number? Solution:
|
| 4. Find the sum of x and y if 3x = 90, and 3y = x.
Solution: Solve 3x = 90 to find x = 30, then solve 3y = x to find y = 10.
Therefore, |
| 5. Find the measure (to the nearest degree) of the acute angle whose tangent is
1.732050808. Solution 1: Put your calculator in degree mode, and compute tan-1(1.732050808),
which should Solution 2: If you recognize that
|
| 6. The average of 11 numbers is 121. When one number is dropped, the average of
the remaining set of numbers is 120. What number was dropped?
Solution: If the average of 11 numbers is 121, their sum must be (11)(121) =
1331. If 10 numbers |
| 7. Give an example of two numbers such that their product is positive, and their
sum is negative. Solution: This is two for any two negative numbers, for example: (−1)(−2) = 2 is
positive, but |
Section B. Each correct answer is worth 2 points.
| 8. Take a three- digit number ending in 1, say ab1. The sum of the digits, a
+b+1, is a two-digit number, cd. The product of those digits, c · d, equals 8. List all possible values for the original number. Solution: If c · d = 8, then the two-digit number cd must be one of these: 18,
81, 24, 42. But |
| 9. A single die ( number cube ) is tossed three times. What is the probability
that all three numbers are the same? Express as a ratio in simplest form .
Solution 1: Here is one line of reasoning: There are 6·6·6 = 63 = 1296 possible
outcomes from Solution 2: Roll the die once. Regardless of how it turns up, there is a 1/6
chance that the second |
| 10. Doc Math chose a two-digit number. He subtracted it from 300 and doubled the
result. Then he added the original two-digit number to this result. What is the largest number that Doc Math could get? Solution: If x is the two-digit number, Doc Math has computed (300 − x) · 2 + x
= 600 − x. |
| 11. While driving, Dale Jr. noticed that his car’s odometer reading, 47974
miles, was a palindrome (reads the same forward as backward). Dale Jr. continued driving, and two hours later the odometer showed the next possible palindrome. What was the average speed of his car during those 2 hours (in mph)? Solution: The next palindrome after 47974 is 48084, 110 miles later. Therefore,
Dale Jr. traveled |
12. Find the largest integer n for which
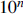 is a factor of
is a factor of
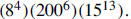
Solution: We have
|
Section C. Each correct answer is worth 3 points.
| 13. In a set of ten whole numbers, the minimum
number is 62, the range is 25, and the median is 82. Find the smallest and largest possible values for the mean of that set of numbers (given to the nearest tenth). Solution: The
answer is 74.5 to 82. The smallest number is 62, the largest is 62 + 25
= 87, and
where
|
| 14. Given a triangle with sides 6, 7, and 9 units, write the length of the
altitude to the shortest side. The answer may be exact, or to the nearest hundredth.
Solution: Given the three side lengths a, b, c of a triangle, we can find its
area using Heron’s |
15.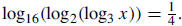 Write the value of x. Write the value of x.
Solution: In general, if
|
| Prev | Next |
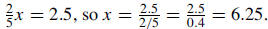
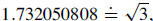 you can
you can 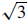 .so that the tangent of the larger acute angle would be
.so that the tangent of the larger acute angle would be
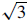 . The hypotenuse
. The hypotenuse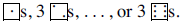 Therefore, the probability that all faces are the same is
Therefore, the probability that all faces are the same is
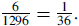
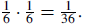
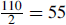 mph.
mph.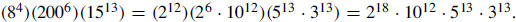 That
That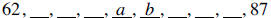
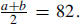 The smallest (or largest) possible means happen when the blanks have the
The smallest (or largest) possible means happen when the blanks have the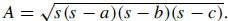
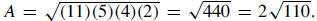 Using the
Using the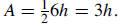
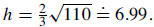
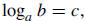 then
then
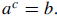 Therefore,
Therefore,
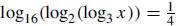 means that
means that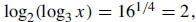 which in turn means that
which in turn means that