Equation Solving IV

A+S 101-003: High school mathematics from a more advanced point of view

1. We’ll proceed with quadratic equations today. We’ll come back to 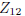 stuff after
quadratics.

2. We need a volunteer to take notes and send them to the email list as an attachment.

3. You received Amy Curl’s wonderful notes on last week’s discussion. (If you need a
hard copy, ask Dr S.) Here are a couple of things Amy brought to light:

• Multiplying both sides of an equation by an expression involving a variable can
result in a change of the domain of the new equation. (Think of multiplying
by 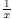, as in the example Brad put forth in Seminar 3; 0 is lost to the domain
of the resulting equation. If 0 is a solution to the original equation, we might
a solution.) What to do in real class time about this? Maybe. put in
parentheses next to the equation that the domain has been messed around
with and when giving the solution set there will have to be accounting for
that.

• Students aren’t always clear about the meaning of “solution” to an equation.
Dr. Jones’ example was interesting (and students do this stuff all the time) :
To solve x ² −3x+2 = 0, students isolate the variable (a great tactic in linear
equations) and solve for x with 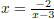. Is that wrong? Hmm.
In the classroom when solving an equation, it will help to provide students
with a clear idea of your expectations.

4. A problem presented last time (but slightly gussied up). Here it is again:

Problem Let E be an equation. Which of the following operations to E results
in an equivalent equation ? If one uses the operation under consideration, what
notations/comments could be made next to the resulting equation?

(a) Adding the same constant to both sides of the equation.

(b) Adding the same algebraic expression to both sides, assuming that involves
only the variables in that algebraic expression are in E also .

(c) Adding the same algebraic expression to both sides of E, assuming the algebraic
expression contains variables not in E.

(d) Squaring both sides of E.

(e) Cubing both sides of E.

(f) Taking the square root of both sides of the equation.

(g) Multiplying both sides of E by the same constant.

(h) Multiplying both sides of E by the same algebraic expression, assuming the
algebraic expression involves only variables contained in E.

Quadratic equations in the real numbers

The algorithm for solving a linear equation with one variable calls for isolating the variable.
Last time we briefly discussed the appropriateness of isolating variables in the quadratic
equation case. We saw that it might not lead to a (numerical) solution to a quadratic but
that students could be expected to do stuff like

x² = −2x + 5.

x² + 2x = 5 (isolate the variable)

x(x + 2) = 5 ( factor out the variable )

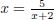Voila!

Of course there’s not all that much wrong with the above procedure. The only problem:
we expected to have a real- number solution (s).

Note. We should expect to see such procedures/solutions from high school students.
As Dr. J pointed out during the first seminar, we ask high school students to solve
x + 2y = 7 for y in terms of x, so a solution that involves x isn’t unheard of. Of course
here with the equation x² = −2x + 5 we expect real number solutions-it’s important to
clarify what is meant by “solution to the equation(s)”.

Okay, so we assume that the student knows what we mean by “solution set” to the
given quadratic equation. Obviously, isolating the variable is not the cleanest way to solve.
So how do we find the numeric solutions to a quadratic?

So, let’s take up a simpler quadratic equation:

x² = 4

This one “talks to us”. It says to me “ a number squared is 4”. Arithmetic facts lead
me to the two solutions {−4, 4}. No prob. Should the “square root word” be invoked here?
There’s some confusion about the meaning of “square root” .these guys can be negative,
versus the square root function.a function with range the non- negative reals . Let’s leave
that for another time.

How about

(x − 1)² = 4?

Or,

(2x − 3)² = 4.

So how can be solve

x² = −2x + 5?

Real-world problem You’re designing a small rectangular city garden. The length
is one less than twice the width. What dimensions should the garden be built so that its
area is 6 square yards? I leave you with the following questions: Could you do a clean,
student-friendly derivation of the quadratic formula? In your most honest moment, do
you think presenting such a derivation, or having students discover it with you, might be
of interest to you and to your students?

It might do some good to bring home to our students that ingenuity was required to solve
quadratic equations. Some human(s), somewhere, quite cleverly finessed the “isolating the
variable doesn’t work” obstruction. Do our students just want to see the “formula” and
get it over with? Might they be able to appreciate that formula if it was presented as a
pretty decent accomplishment? Or let them discover themselves how to do the “finessing”
?

Question. Do you think it would be helpful/useful to derive the quadratic formula,
perhaps jointly with your students? Have you ever tried yourself to derive it and/or
thought about its derivation and its validity?