NUMBER THEORY

1999-A-6. The sequence 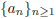is defined by 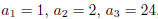and for n ≥ 4,

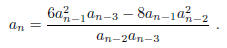
Show that, for all n, a_n is an integer multiple of n.

1999-B-6. Let S be a finite set of integers, each greater than 1. Suppose that for each integer n there
is some s ∈ S such that gcd (s, n) = 1 or gcd (s, n) = s. Show that there exists s, t ∈ S such that gcd (s, t)
is prime. [Here gcd (a, b) denotes the greatest common divisor of a and b.]

1998-A-4. Let A₁ = 0 and A₂ = 1. For n > 2, the number A_n is defined by concatenating the
decimal expansions of 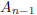and 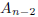from left to right. For example,
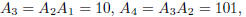
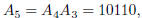and so forth. Determine all n such that 11 divides A _n.

1998-B-5. Let N be the positive integer with 1998 decimal digits, all of them 1; that is, N = 1111 · · · 11
(1998 digits). Find the thousandth digit after the decomal point of

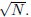
1998-B-6. Prove that, for any integers a, b, c, there exists a positive integer n such that
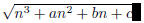
is not an integer.

1997-A-5. Let N_n denote the number of ordered n−tuples of positive integers (a₁, a₂, · · · , a_n) such
that 1/a₁ + 1/a₂ + · · · + 1/a_n = 1. Determine whether 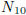is even or odd.

1997-B-3. For each positive integer n write the sum 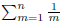in the form 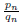where p_n and q_n are
relatively prime positive integers . Determine all n such that 5 does not divide q_n.

1997-B-5. Prove that for n ≥ 2,

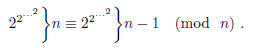
1996-A-5. If p is a prime number greater than 3, and 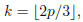prove that the sum

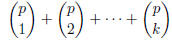
of binomial coefficients is divisible by p².
(For example,)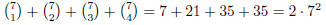

1995-A-3. The number d₁d₂ · · · d₉ has nine (not necessarily distinct) decimal digits. The number
e₁e₂ · · · e₉ is such that each of the nine 9-digit numbers formed by replacing just one of the digits d_i in
d₁d₂ · · · d₉ by the corresponding digit e_i (1 ≤ i ≤ 9) is divisible by 7. The number f₁f₂ · · · f₉ is related
to e₁e₂ · · · e₉ in the same way; that is, each of the nine numbers formed by replacing one of the e_i by
the corresponding f_i is divisible by 7. Show that, for each i, d_i − f_i is divisible by 7. [For example, if
d₁d₂ · · · d₉ = 199501996, then e₆ may be 2 or 9, since 199502996 and 199509996 are multiples of 7.]

1995-A-4. Suppose we have a necklace of n beads. Each bead is labelled with an integer and the sum
of all these labels is n − 1. Prove that we can cut the necklace to form a string whose consecutive labels x₁,
x₂, · · ·, x_n satisfy

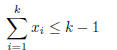for k = 1, 2, · · · n .

1994-B-1. Find all positive integers that are within 250 of exactly 15 perfect squares. (Note: A perfect
square is the square of an integer; that is, a member of the set {0, 1, 4, 9, 16, · · · , }. a is within n of b if
b − n ≤ a ≤ b + n.)

1994-B-6. For any integer a, set 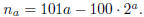Show that for 0 ≤ a, b, c, d ≤ 99,

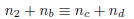(mod10100)

implies {a, b} = {c, d}.

1993-A-4. Let 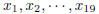be positive integers each of which is less than or equal to 93. Let
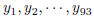be positive integers each of which is less than or equal to 19. Prove that there exists a
(nonempty) sum of some x_i’s equal to a sum of some y_j ’s.

1993-B-1. Find the smallest positive integer n such that for every integer m, with 0 < m < 1993, there
exists an integer k for which

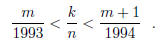
1993-B-5. Show there do not exist four points in the Euclidean plane such that the pairwise distances
between the points are all odd integers.

1993-B-6. Let S be a set of three, not necessarily distinct, positive integers. Show that one can
transform S into a set containing 0 by a finite number of applications of the following rule: Select two of the
three integers, say x and y, where x ≤ y, and replace them with 2x and y − x.

1992-A-3. For a given positive integer m, find all triples (n, x, y) of positive integers, with n relatively
prime to m, which satisfy

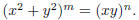
1992-A-5. For each positive integer n, let

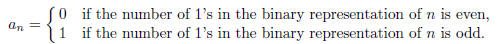
Show that there do not exist positive integers k and m such that

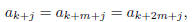for 0 ≤ j ≤ m − 1 .

1989-A-1. How many primes among the positive integers, written as usual in base 10, are such that
their digits are alternating 1’s and 0’s, beginning and ending with 1?

1988-B-1. A composite (positive integer) is a product ab with a and b not necessarily distinct integers
in {2, 3, 4, · · ·}. Show that every composite is expressible as xy + xz + yz + 1, with x, y, and z positive
integers.

1988-B-6. Prove that there exist an infinite number of ordered pairs (a, b) of integers such that for
every positive integer t the number at +b is a triangular number if and only if t is a triangular number. (The
triangular numbers are the t _n = n(n + 1)/2 with n in {0, 1, 2, · · ·}.

1987-A-2. The sequence of digits

1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 9 2 0 2 1 · · ·

is obtained by writing the positive integers in order . If the 10ⁿ-th digit in this sequence occurs in the part of
the sequence in hich the m− digit numbers are placed, define f(n) to be m. For example f(2) = 2 because
the 100th digit enters the sequence in the placement of the two digit integer 55. Find, with proof, f(1987).