NUMBER SENSE
NUMBER SENSE : Fractions and Decimals
The Winning EQUATION
A HIGH QUALITY MATHEMATICS PROFESSIONAL DEVELOPMENT
PROGRAM FOR TEACHERS IN GRADES 4 THROUGH ALGEBRA II

STRAND: NUMBER SENSE: Fractions and Decimals
MODULE TITLE: PRIMARY CONTENT MODULE VI
MODULE INTENTION: The intention of this module is to inform and instruct
participants in
the underlying mathematical content in the areas of fractions and decimals.
THIS ENTIRE MODULE MUST BE COVERED IN-DEPTH.
The presentation of these Primary Content Modules is a departure from past
professional
development models. The content here, is presented for individual teacher’s
depth of
content in mathematics. Presentation to students would, in most cases, not
address the
general case or proof, but focus on presentation with numerical examples.
In addition to the underlying mathematical content provided by this module, the
facilitator
should use the classroom connections provided within this binder and referenced
in the
facilitator’s notes.
TIME: 2 hours
PARTICIPANT OUTCOMES:
•· Demonstrate understanding of fractions and decimals.
• Demonstrate understanding of the relationships of fractions and decimals.
• Demonstrate how to convert fractions to decimals and decimals to fractions for
repeating
and non-repeating decimals.
| Pre- Post-Test T-1 H-1 |
PRIMARY CONTENT MODULE VI
NUMBER SENSE: Fractions and Decimals
Facilitator’s Notes
Ask participants to take the pre-test. After reviewing the results of the
pre-test proceed with the following lesson on fractions and decimals.
Arithmetic provides two ways of representing non-whole numbers:
decimals and fractions. An understanding of the connections between
these notations is an important part of arithmetic. While the ability to
transform decimals into fractions and fractions into decimals is a
practical skill of importance in itself, it also leads to some profound
insights into the concept of "number."
Recall the decomposition of whole numbers in powers of ten. An
example is
428 = 4 • 100 + 2 • 10 + 8 • 1
Decimals Into Fractions: By recalling their definition in terms of
powers of 10, the problem of transforming decimals into fractions
becomes straightforward. Facilitator should guide teachers through
each step in this example . For example, to express .428 as a fraction
we recall that
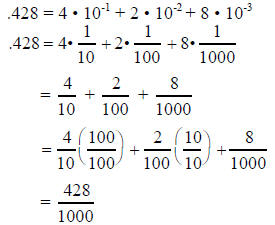
One representation of .428 in fractional form is 428/1000.
In order to
reduce this fraction to lowest terms, we note that GCD(428, 1000) = 4.
Dividing top and bottom by 4 we obtain a fraction in simplified form .
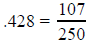
Have participants do H-1 for practice converting decimals to fractions.
| T-2 H-2 T-3 T-4 T-5 |
Fractions Into Decimals: One way of obtaining "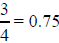 "
is by long
"
is by long
division. Recalling that one interpretation of the fraction a/b is "the
answer to the division problem a ÷ b ." We carry out the division
process 3 ÷ 4 as follows:
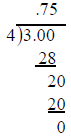
Have participants do H-2 for practice converting fractions
to decimals.
But why does dividing numerator by denominator give the correct
decimal? When converting a fraction into a decimal by dividing
numerator by denominator, we essentially find an equivalent fraction
whose denominator is a power of 10, i.e. a fraction of the form:
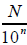
In the case of 3/4, we are to find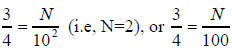
(How do we know to use 100 for the searched equivalent
fraction?
We’ll come back to this question.) Solve N, we use cross
multiplication.
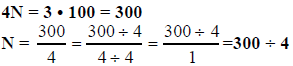
Then using long division, we obtain N=75. Long division shows
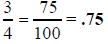
Note, however, not all fractions may have an equivalent
fraction
whose denominator is a power of 10. Fractions like
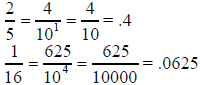
have corresponding terminating decimal forms.
| T-6 T-7 T-8 |
Other fractions can only be converted into decimals with
an infinite
number of decimal places.
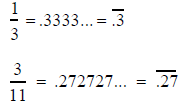
How can we tell if a fraction can convert into a
terminating decimal?
Answer: For any fraction a/b that is written in the lowest terms, it can
be shown that the corresponding decimal terminates only when
b = 2m • 5n for m, n = 0, 1, 2, … Note: m or n could be
zero.
As shown above, a terminating fraction equals a fraction whose
denominator is a power of 10. Also recall that (cd)n = an
bn from
Module 1. Therefore, 10n = (2 • 5)n = 2n • 5n.
This means that the only
prime factors of 10n are 2 and 5.
In order for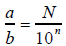 , we must multiply a and
b by some whole
, we must multiply a and
b by some whole
number, let’s say, k so that the answer is bk = 10n. Since
bk = 10n =
(2 • 5)n = 2n • 5n, we can conclude, that b
(as well as k) has only prime
factors of 2 and/or 5.
For example,
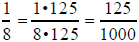
or 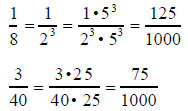
or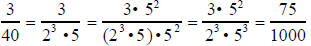
This also explains why, in the case of 3/4, we chose to convert it to
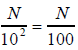 because
because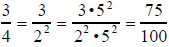
| T-9 T-10 |
Fractions Into Repeating Decimals: The second
method described
above made use of the fact that, when written in lowest terms, the
denominators of
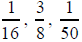 , and
, and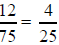 all
have prime
all
have prime
factorizations consisting only of 2s and 5s. For fractions such as 1/3,
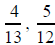 , it is impossible to transform them into
terminating decimal
, it is impossible to transform them into
terminating decimal
form.
It is possible to use long division to relate such fractions to a repeating
form in decimal notation. Here we use long division to show that
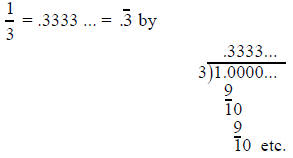
Indeed, long division shows that it is possible to convert
any fraction
a/b into a terminating or a repeating decimal. Regarding a/b as the
solution of a division problem of the form a ÷ b, we note that long
division eventually involves "bringing down zeros." These zeros are
appended to remainders that are whole numbers smaller than the
divisor b. Thus, in the course of at most b divisions we must have a
remainder that appeared before. When this occurs, we fall into a
repeating pattern that leads to a repeating decimal representation for
a ÷ b.
By way of example,3/11 corresponds to the long division problem
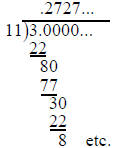
The fact that we alternate between remainders of 8 and 3
shows that
the pattern .272727 ... will repeat indefinitely and that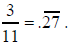
| T-11 H-3 T-12 H-3A |
Ask participants to find the decimal for 1/7 and explain
why it must
have a repeating block. The repeating decimal pattern corresponding
to 4/13 is not revealed by the first eight digits of its decimal expansion.
However, even without knowing what the repeating decimal is, long
division assures the existence of a pattern of length at most 12.
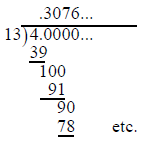
The reason is that in applying the long division
algorithm, the dividend
4 is written with an unending string of zeros to the right of the decimal
point. Each time we apply the algorithm to obtain a new digit in the
quotient, we obtain a remainder that is less than 13. Since the numbers
0 through 12 are the only possible remainders, 12 applications of the
division process are sure to lead either to a remainder of zero (in which
case we have a terminating decimal), or else to a positive remainder that
has occurred previously. Since we are always bringing down zeros, a
repeated remainder leads to an operation identical with one that has
occurred before. As a result, this operation is followed by a pattern that
will repeat indefinitely. This gives us the following point to consider.
A Point to Consider: The number of places in a repeating pattern is, at
most, 1 less than the divisor.
Have participants do worksheet H-3A on repeating decimals.
We have seen that reduced fractions of the form a/b correspond to
terminating decimals whenever b has prime factorization of the form
2m ×5n . For fractions whose decimal expansion fails to
terminate, long
division assures that a/b corresponds to a repeating decimal. By
regarding terminating decimals as a special kind of repeating decimal;
i.e., one whose repeating pattern consists of zeros - one can assert that
all fractions correspond to repeating decimals.
| T-14 T-15 H-4 |
Repeating Decimals into Fractions: If you didn’t already know that
 how could you deduce
it?
how could you deduce
it?
Let:
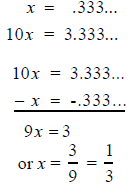
This technique works for longer repeating patterns as
well. For
example, to evaluate 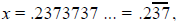 we note that
we note that

An easier way to do this might be to consider having only
the
repeating portion to the right of the decimal, then when you subtract,
you will always get a whole number for the numerator.
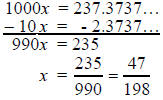
Have participants do worksheet H-4 to convert these
decimals to
fraction form: .888 ... ; .232323 ... ; .311311311 ... ; .763545454 ... .
Theorem
Irrational Numbers: The fact that fractions correspond to terminating
or repeating decimals and vice-versa has profound consequences.
Non-repeating decimals such as .101001000100001000001 ....
correspond to numbers that are not rational. Conversely, "irrational"
numbers such as
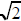 correspond to decimals that fail to repeat.
correspond to decimals that fail to repeat.
| T-18 H-5 T-19 |
The fact that a number is rational if and only if its
decimal
representation has a repeating block can also be used to show that the
irrational numbers are "dense" in the following sense: Given any two
rational numbers, there exists an irrational number between them. For
example, an irrational number between 1/4 and .26 is given by
.2501001000100001 ... .
Have participants do worksheet H-5 to find an irrational number
between 1/2 and .5001. One of many possible answers is:
0.500 01 001 0001 000001…
While a full discussion of such "irrational numbers" is not called for in
the standards, the study of long division and the correspondence
between decimals and fractions sets the stage for an understanding of
this profoundly important part of mathematics.
Show the chart on T-19.
Administer the post-test.
Fractions and Decimals
Pre- Post-Test
Convert each fraction to a decimal:


Convert each decimal to a fraction:


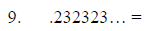
Fractions and Decimals
Pre- Post-Test Answer Key

Decimals to Fractions
Recall:
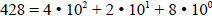
We can use this same process to change .428 to a
fraction
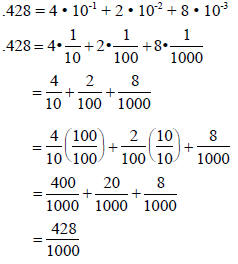
This can be reduced using GCD(428, 1000) = 4

Fractions and Decimals
Worksheet
Convert these decimals to fraction form:
.6 =
.415 =
.503 =
Fractions to Decimals
The fraction a/b is
“the answer to the division problem a ÷ b.”
So 3/4 can be converted to its decimal equivalent by
dividing 3 by 4.
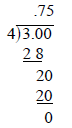
Fractions and Decimals
Worksheet
Convert these fractions to decimal form:
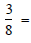
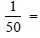
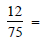
Fractions to Decimals
Why does dividing numerator by denominator
give the correct decimal?
When converting a fraction into a decimal by
dividing numerator by denominator, we essentially
find an equivalent fraction whose denominator is a
power of 10, i.e., a fraction of the form:
![]()
In the case of 3/4 , we choose n = 2. Thus,
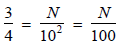
Fractions to Decimals
Why does dividing numerator by denominator
give the correct decimal?
To find an equivalent fraction for 3/4, set
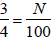
Use cross multiplication:
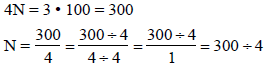
Then use long division to obtain N = 75. That is,
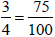
This is why long division yields
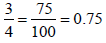
But, how do we know which power of 10 to use in
the denominator, e.g. 102 for 3/4?
Fractions to Decimals
Not all fractions may have an equivalent fraction
whose denominator is a power of 10. Fractions
like:
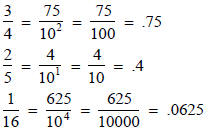
have corresponding terminating decimal forms.
But other fractions can only be converted into
decimals with an infinite number of decimal
places
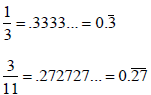
etc.
Fractions to Decimals
Question: How can we tell if a fraction can be
converted into a terminating decimal?
Answer: A fraction a/b that is written in the lowest
terms can be converted into a terminating decimal
if and only if b = 2m • 5n for m, n = 0, 1, 2,… In
other words, if and only if the prime factors of b
are 2 and/or 5.
Rationale: As shown above, a terminating decimal
is a fraction whose denominator is a power of 10.
That is,
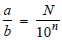
Recall that (cd)n = cndn
from Module I.
Therefore,
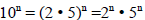
This means that the only prime factors of 10n
are
2 and 5.
Fractions to Decimals
In order for 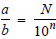 we must
multiply a and b by
we must
multiply a and b by
some whole number k so that ak = N and bk=10n.
That is,

Since bk = 10n = 2n • 5n,
we conclude that b (as
well as k) has only prime factors of 2 and/or 5.
For example,
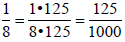
or 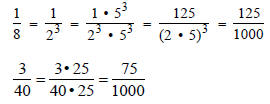
or 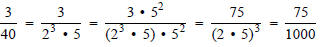
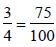 Revisited
Revisited
In the argument that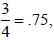 using long division,
using long division,
we wrote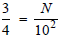 Why 102?
Why 102?
Answer:
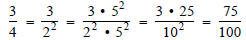
Since 4 = 22 , we needed a factor of 5 to the
same
power.
Note: Any higher power of 10 would also work,
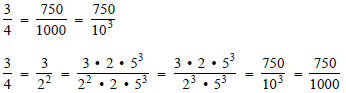
This may be reduced to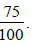
Fractions Into Repeating Decimals
Long division converts some fractions to repeating
decimals.
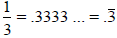 by doing long division
for 1 ÷ 3
by doing long division
for 1 ÷ 3
4/13and 5/12 also have infinite decimals because the
denominators have prime factors other than 2 and 5.
Example:
Converting 3/11 to a decimal corresponds to
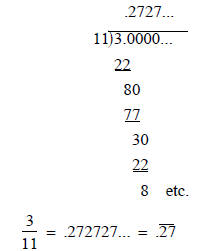
Assignment
Use long division to find the decimal for1/7. Be
prepared to explain why the decimal has a repeating
block to the other teachers here today.
What feature of the standard long division
algorithm is crucial to your argument?
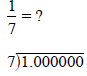
What is the maximum number of digits in a
repeating block in relation to the divisor?
A calculator will not show 4/13 as a repeating decimal.
Long division determines the repeating pattern.
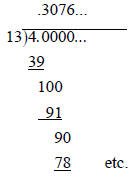
Fractions and Decimals
Worksheet
Continue the long division problem. At which
point does it repeat?
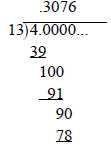
Is 5/17a repeating or terminating decimal?
Show how you determined your answer
Terminating Decimals
Terminating decimals can be regarded as a special
kind of repeating decimal
with a repeating pattern of zeros.
Converting 3/4 to a decimal using long division
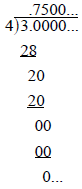
means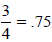
So, all fractions correspond to repeating decimals.
Repeating Decimals to Fractions
If you didn’t already know that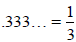 ,how
,how
could you deduce it?
Let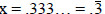
Then
Then 10x = 3.333…
Subtract x from both sides.
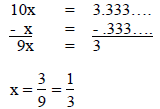
For more complicated decimals, this also works:
Evaluate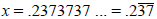
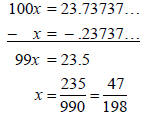
An easier way is to consider having only the
repeating portion to the right of the decimal.
Fractions and Decimals
Worksheet
Convert these decimals to fraction form:
.888 ... =
.232323 ... =
.311311311 ... =
.763545454 ... =
Theorem
Combining the algebraic method for converting
repeating decimals to fractions with the long
division argument gives this important result:
Theorem – Any fraction is equal to a decimal with
a repeating block, and any decimal with a repeating
block is equal to a fraction.
What about infinite decimals without repeating
blocks?
Irrational Numbers
Not all decimals have repeating blocks. Look
carefully at
.101001000100001…
This decimal has no repeating block. It is an
example of an
Irrational Number
An irrational number is an infinite decimal which
has no repeating block. Another example is
![]()
but it requires a careful argument to show this.
Real Numbers
The set of real numbers is the set of all rational
numbers together with the set of all irrational
numbers.
Between any two different real numbers is a
rational number and an irrational number.
Example: One irrational number between
1/4 and .26
is: .2501001000100001…
A rational number between
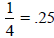 and .26 is
and .26 is
.255 or 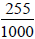
Fractions and Decimals
Worksheet
Find an irrational number between 1/2 and .5001.
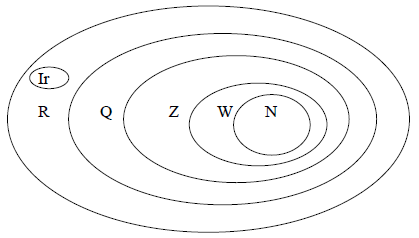
Sets of numbers

N: natural numbers (counting numbers)
W: whole numbers (natural numbers and 0)
Z: integers
Q: rational numbers
R: real numbers
Ir: irrational numbers
Fractions and Decimals
Pre- Post-Test Answer Key




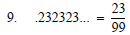
Fractions and Decimals
Worksheet Answer Key
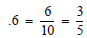
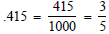
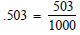
Fractions and Decimals
Worksheet Answer Key
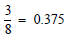

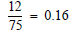
Assignment
Answer Key
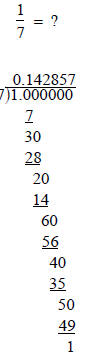
Fractions and Decimals
Worksheet Answer Key

Fractions and Decimals
Worksheet Answer Key
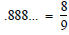
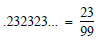
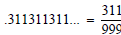
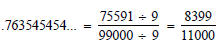
Fractions and Decimals
Worksheet Answer Key

For instance,
.50001010010001
| Prev | Next |