MATH 130 REVIEW FOR TEST 3

TEST POLICIES (REMINDERS)

If you know that you will be absent on the day of a test, it may be possible to make arrangements with me to take
the test on an earlier day. This alternative is not automatic!! Each case will be considered individually. You should
notify me as soon as possible regarding planned absences. There are no make-up exams provided for unexpected
absences. If you miss an exam for an unexpected absence, the average that you earn on the final will make-up the
score for your missed exam. There are no exceptions – do not ask!!

HONOR POLICY:

You must observe the following rules during any in class exam or quiz.
(1) You will be assigned a seat on the day of the exam.
(2) Be prepared to move to your designated seat.
(3) You are not permitted to leave the room.
(4) You must not look anywhere in the room other than at your own test paper.
(5) You may not use or even touch a cell phone.
Remember your cell phone is always silenced in class.
(6) You may not speak to another student.
(7) You may not share materials with another student.
(8) Have all your materials ready. You may not retrieve items from your backpack etc.

Failure to observe all of the policies will result in a zero score for the test or quiz.

When you complete a test, you will hand it to me personally. You may leave the room at this time and
return (if necessary) at the planned time. The only questions permitted during an exam is in reference to
a misprint, omission, or illegible text. You are responsible for being prepared for the exam. You do not
have the time to figure out problems on exam day. You must turn in your test paper when time is called.
I will give a five minute warning before collecting exams. If you do not hand in your paper at that time, I
will not accept it later. It is your responsibility to keep track of time during the exam.

TEST REVIEW PROBLEMS

This test review will give you an idea of the difficulty level of the problems that will
be on the exam. This test review contains a sample problem from every topic that
will be covered on the exam. Test problems will be similar, but not identical. if you
have done all the homework, asked for help as needed, and reviewed the material
diligently, you should now find this review easy to moderate to complete. If you
struggle with the review, we will go over some solutions in class . However, please
be aware that your struggle is an indication that you should go back to the
homework sets and work additional problems similar to those on this review in order
to perform well on the exam.

The problems begin on the next page. The answers are included at the end of the review.

Chapter 4
1. If a number W divides 300 and W divides 50, will W divide 350? Provide a
counterexample or state the name of the theorem that supports the claim.

2. If a number V divides 450 and V divides 50, will V divide 400? Provide a counterexample
or state the name of the theorem that supports the claim.

3. If a number X divides 30, will X divide 300? Provide a counterexample or state the
name of the theorem that supports the claim.

4. If a number Y divides 24, will divide 8 and 3? Provide a counterexample or state the
name of the theorem that supports the claim.

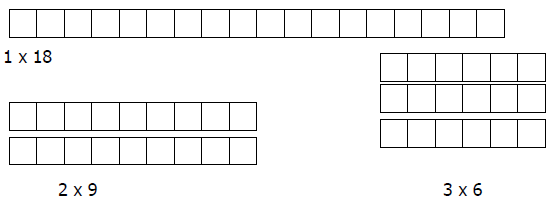
5. Use rectangles to show all pairs of factors of 18.

6. Fill in the blank with all possible digits so that the number: 457_ is divisible by
A. 2
B. 3
C. 4
D. 5
E. 6
F. 8
G. 9
H. 10

7. Are the following statements true or false? If the statement is true, justify your answer
using terms from Chapter 4. If the statement is false, provide a counterexample.
A. If a number is divisible by 3 and 5, then it is divisible by 15.
B. If a number is divisible by 2 and 6, then it is divisible by 12.

8. Give two examples of factors of 40.

9. Give two examples of multiples of 40.

10. Find the following:
A. The prime factorization of 210
B. The prime factorization of 63
C. GCF (210, 63)
D. LCM (210, 63)

11. If p = 2⁸ x 3⁷ x 5⁸ x 11 and q = 2 x 3⁵ x 7 x 11 x 13, find (leave answers in factored form)
A. GCF (p, q) B. LCM (p, q)

12. If p = r¹⁷s²²t⁵u¹⁸v⁷²w²³x²yz⁴ and q = r⁴s⁵t⁶u⁷v⁸wx⁹y¹⁰z²⁰, find (leave answers in factored
form)
A. GCF (p, q) B. LCM (p, q)

13. Jane and Tom were giving a dinner party, and Jane was making hors d’oeuvres. Because
one couple had not yet responded, she wasn’t sure whether there would be 8 or 10
people (including herself and Tom) at the party. In either case, Jane wanted to make
enough hors d'oeuvres for each person to have an equal number. What is the smallest
number she could make?

14. Arturo and Samantha are riding their bikes around a course. They start at the same time,
but Arturo takes eight minutes to complete a lap, while Samantha only takes six minutes
for each lap. After how many minutes with they meet at their starting point again?

15. Mr. Knot has two lengths of rope which he wants to cut into equal pieces, each as long as
possible for his cub scout troop to use to practice tying knots. He doesn’t want to have
any short pieces left over. If one length of rope is 75 inches long and the other is 135
inches long,
A. what length pieces should be cut?
B. how many pieces will he have?

16. Give an example of two composite numbers that are relatively prime (to each other).

Chapter 5
17. Perform the following operations :
A. |-5 - (-4)|
B. (-4)(-5) + (3)(-2)
C. 3(-2) + (-5)(-6)
D. 4(-3)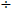 -2 X -5

18. Explain how to compute -6 - 3 using: (Draw a pictorial model)
A. a number line
B. signed counters

19. Explain how to compute 4 - (-2) using: (Draw a pictorial model)
A. a number line
B. signed counters

20. Make up a temperature or money problem for 5 - 8.

21. Write an application problem that is solved by computing -4 x (-10).

22. Write an application problem that is solved by computing -8 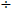2,

23. Suppose you have a student who turns in the following problems. What misconception
does the child have?
-5 + 3 = -8
-3 + (-2) = -5
7 + (-2) = 9

24. Suppose you have s student who turns in the following problems:
-5 + 3 = -8
-3 + (-2) = 5
7 + (-2) = -9
A. What would you expect the child to answer for the following:
-4 + (-5) = __________ -4 + 5 = ____________
B. What misconception does the child have?

25. The temperature dropped 15 degrees from the high temperature to reach a low
temperature of ;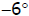C. What was the high temperature? Write an equation and solve it.

26. Fill in the property that justifies each step .
3 x 4 = 3 x (4 + 0) _______________________________
3 x (4 + 0) = (4 + 0) x 3 _______________________________
(4 + 0) x 3 = (4 + (5 + -5)) x 3 _______________________________
(4 + (5 + -5)) x 3 = ((5 + -5) + 4) x 3 _______________________________
((5 + -5) + 4) x 3 = (5 + (-5 + 4)) x 3 _______________________________
(5 + (-5 + 4)) x 3 = 5 x 3 + (-5 + 4) x 3 _______________________________

ANSWERS:

1. Yes, Divisibility of a sum
2. Yes, Divisibility of a difference
3. Yes, Divisibility of a product
4. No; 6 divided 24, but 6 does not divide 8 or 3.
5.

6.
A. 0, 2, 4, 6, 8
B. 2, 5, 8
C. 2, 6
D. 0,5
E. 2,8
F. 6
G. 2
H. 0
7. A. True, a number that is divisible by 15 must contain its prime factorization 3 x 5.
B. False, many counterexamples: 6 is the minimum number which is divisible by 2 and
6 but not by 12.
8. Any two of 1, 2, 4, 5, 8, 10, 20, or 40
9. Any two of 40, 80, 120, 160, ….

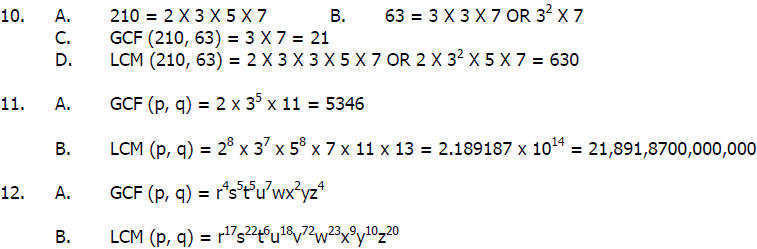
13. LCM (8, 10) = 40. The smallest number of hors d’oeuvres Jane should prepare is 40.

14. LCM(8, 6) = 24. Samantha and Arturo will meet at the starting point in 24 minutes.
15.
A. GCF (75, 135) =15. Mr., Knot should cut the rope into pieces 15 inches long.
B. He would get (75 + 135)/15 = 14 pieces each 15 inches long.

16. 15 and 16 provide one example. You can choose any pair of numbers so that their GCF is
one.

17. A. |-5 + 4| = |-1| = 1
B. 20 + -6 = 14
C. -6 + 30 = 24
D. -12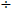 (-2)(-5) = 6(-5) = -30

18.
A. Go to -6 on the number line. Then move left 3 places to -9. Thus, -6 – 3 = -9.

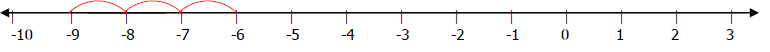
B. Use six negative counters to represent -6. You can’t take away 3, so add 3 pairs of
positive and negative counters. Now take away three positive counters. There are
9 negative counters left. So
-6 – 3 = -9.

19. A. Go to 4 on the number line. You would move left two places for -2, but since you
are subtracting , reverse the direction and move right 2 places to 6. 4 – (-2) = 6.

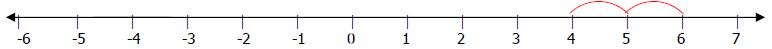
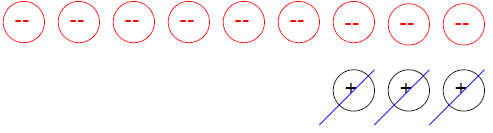
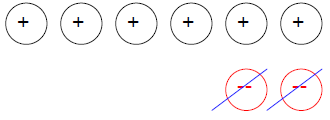
B. Use four positive counters to represent 4. You can’t take away -2 so add two pairs
of positive and negative counters. Now take away 2 negative counters. There are
six positive counters left.
-4 – (-2) = 6.

20. One day in December the temperature was 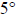F at sundown and then it fell 8 F in the
evening. What is the new temperature?

21. You have spent $10 an hour on lottery tickets and you now have no money left. How
much money did you have 4 hours ago?

22. The temperature has dropped 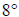in two hours. What is the average change in
temperature each hour?

23. The child is adding the absolute values of the numbers and affixing the sign of the number
with the larger absolute value.
24. A. -4 + (-5) = 9
-4 + 5 = -9
B. The child appears to be using the rules for signs that are used for multiplication
with these addition problems. The child is consistently giving a positive result when
the signs are the same, and a negative result when the signs are different .

25. H – 15 = -6 so H = 15 + (-6) = 9. The high temperature was 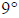C.

26. Identity Property for Addition, Commutative Property of Multiplication, Property of Additive
Inverses, Commutative Property of Addition, Associative Property of Addition, Distributive
Property of Multiplication over Addition