QUICK INTRODUCTION TO MATLAB
General Remarks
This worksheet is designed for use with MATLAB version 6.5 or later. Once you
have
MATLAB running on your machine, you get MATLAB to do things for you by typing
commands at the prompt sign ">>".
There are various forms of help available. Typing
helpwin, helpdesk, or demo opens an interactive help window
help <function_name> lists the description of <function_name> in the command
window
diary on, diary off - record all activities on the command window into a file
named
"diary" (e.g. for assignments)
diary <filename> - save your session in a file named "<filename>". If the
file already
exists, the new listing is appended.
Matrices
The basic object in MATLAB is a matrix (hence the name, MATtrix LABoratory). The
entries
of a matrix are complex numbers .
There is no limitation on the size of the matrix (number of rows and number of
columns).
Scalars are treated as 1x1 matrices.
To type a matrix into MATLAB
use square brackets "[" and "]"
separate elements in a row with commas "," or
spaces " "
use a semicolon ";" to separate rows.
For example, type
[1 2 3;4 5 6;7 8 9]
ans =
1 2 3
4 5 6
7 8 9
[2+3*i; pi; exp(1)]
ans =
2.0000 + 3.0000i
3.1416
2.7183
All computations are performed in double precision. The
format commands switch
between different output formats:
format short; pi % 4 decimal digits
ans =
3.1416
format long; pi % 14 decimal digits
format short e; pi % 4 decimals in exponential nonation
format long e; pi % 14 decimals in exponential notation
ans =
3.14159265358979
ans =
3.1416e+000
ans =
3.141592653589793e+000
Alternatively, you can tell num2str how many digits to display
num2str(pi, 3)
ans =
3.14
MATLAB has several ways to generate simple matrices (need to specify the size)
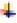zeros - matrix with all elements equal to
zero
ones - matrix with all
elements equal to one
eye – identity matrix
rand – matrix with
uniformly distributed random elements
randn - matrix with
normally distributed random elements
Examples to try:
zeros(2,3), ones(2,2), eye(3)
ans =
0 0 0
0 0 0
ans =
1 1
1 1
ans =
1 0 0
0 1 0
0 0 1
Variables
Variables in Matlab are named objects that are assigned using the equal sign
"=". They
may contain upper and lowercase letters ,
any number of "_" characters and numerals, but cannot start with a numeral.
names and types of
variables do not have to be declared apriori.
names of variables
should not overlap with MATLAB keywords, function names
and command names
Scalar variables can
be later extended into vectors and matrices
Examples of valid MATLAB variable assignments:
a = 1
ind = [1 3 5 7]
Output_Type1 = v*Q*v'
name='John Smith'
The following are bad choices for variable names
2for1 = 'yes'
end = 1
sin = 10
i = 2
clear
<variable_name> - delete the value of <variable_name> from the current
working space
clear all - clear
values of all variables
clc - clear the
command window and move the cursor to the top
Common Operators
Semicolon ";" is used
to assign a variable without getting an echo from MATLAB.
Comma "," separates
different commands on the same line, the result is printed
for each command
Colon ":" generates an
ordered set of numbers
Three periods "…"
split a long command into several lines.
Comment sign "%" makes
MATLAB ignore the whole line after the sign, hence is
used for comments.
Try the following:
a = 2
b = 3;
c = a+b;
d = c/2;
c, d
who % Lists all variables defined so far
whos
clear % Clears all previously defined variables
f = 1:5;
who
Arithmetic Operations
"+", "-", "*", "/" –
conventional operators for addition , substraction,
multiplication and division
"\" – inverse division
(3\2 = 2/3 = 0.6666)
"^" – power operator
Type the following
r = 10;
vol = 4*pi ...
*r^3/3;
r,vol
r =
10
vol =
4.1888e+003
".*", "./" –
multiplication and division between the elements of two matrices of
the same dimension
".^" – power operation
for each element of the matrix
Try the following commands
A = [1 2;3 4], B=2*ones(2)
A.^2, A.*B %Note that these are not the same as A^2 and A*B
A =
1 2
3 4
B =
2 2
2 2
ans =
1 4
9 16
ans =
2 4
6 8
Vectors
A vector is a one-dimensional array, which is a matrix consisting of one column
(column
vectors) or of one row (row-vectors).
MATLAB code is designed to handle matrices (in particular vectors) in an optimal
way, and
it contains an extensive list of operations
with vectors/matrices. Let's start learing the most elementary ones.
Consider the row
vector x and the column vector y as follows
x = [ 0, 0.5, 1, 1.5, 2] , y=[0; 2; 4; 3; 1]
x =
0 0.5000 1.0000 1.5000 2.0000
y =
0
2
4
3
1
Toaccess individual
elements, try
x(2), y(3)
ans =
0.5000
ans =
4
x(6)
??? Index exceeds matrix dimensions.
y(0)
??? Subscript indices must either be real positive integers or
logicals.
x(2:4) % reduces the dimension of x by retaining only the elements
ranked 2 thru 4
y(end-2:end) % reduce the dimension of y and retain only the last
three elements
ans =
0.5000 1.0000 1.5000
ans =
4
3
1
One can extract rows
and columns from a given matrix. For example
a = [1 2 3;4 5 6;7 8 9]
a =
1 2 3
4 5 6
7 8 9
a(:,2), a(3,:)
ans =
2
5
8
ans =
7 8 9
Conversely, one can
generate new matrices by concatenating old
vectors/matrices:
b = [a -a; a(3,:) zeros(1,3)]
b =
1 2 3 -1 -2 -3
4 5 6 -4 -5 -6
7 8 9 -7 -8 -9
7 8 9 0 0 0
To list all the
elements of a matrix and form a row vector, type
a(:)'
ans =
1 4 7 2 5 8 3 6 9
Note that the listing starts with the elements on the first column, then the
second and the
third!
An equally-spaced vector x can be defined using the colon operator ":"
x = 0:0.5:2 % (first element, step size, last element)
x =
0 0.5000 1.0000 1.5000 2.0000
Another example is
t = 0:.3:2*pi
t =
Columns 1 through 7
0 0.3000 0.6000 0.9000 1.2000 1.5000 1.8000
Columns 8 through 14
2.1000 2.4000 2.7000 3.0000 3.3000 3.6000 3.9000
Columns 15 through 21
4.2000 4.5000 4.8000 5.1000 5.4000 5.7000 6.0000
Another way to
generate an equally-spaced vector is using the 'function'
"linspace".
x=linspace(0,0.25,5) % linspace (first element, last element, number of
elements)
x =
0 0.0625 0.1250 0.1875 0.2500
Pointwise multiplication, division and pointwise power:
x=[1,2,3]; y=[0,2,-1];
x.*y % multiplies pointwise two vectors of the same size
x./y % no loops required for accessing individual elements
ans =
0 4 -3
Warning: Divide by zero.
(Type "warning off MATLAB:divideByZero" to suppress this warning.)
ans =
Inf 1 -3
x.^2
x.^y % same as x(k)^y(k) for every k
3.^x % same as 3^x(k); the output has same size as x
ans =
1 4 9
ans =
1.0000 4.0000 0.3333
ans =
3 9 27
These operation are one of the main advantages of MATLAB, since they do not
require
involving loops.
Basic Graphics
The most efficient way of representing the outcome of a numerical computation is
to plot
the data.
Here are a few examples of MATLAB plots.
x = 0 : 0.3 : 2*pi; % low resolution
y = exp(-x).*sin(2*x);
plot(x,y)
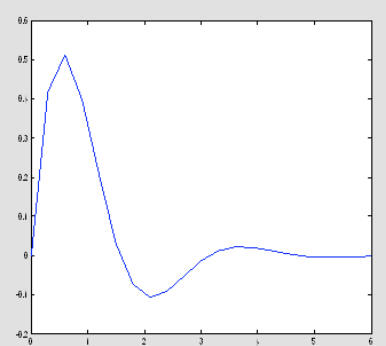
A better resolution is obtained below
x = 0 : 0.1 : 2*pi; % higher resolution
y = exp(-x).*sin(2*x);
plot(x,y)
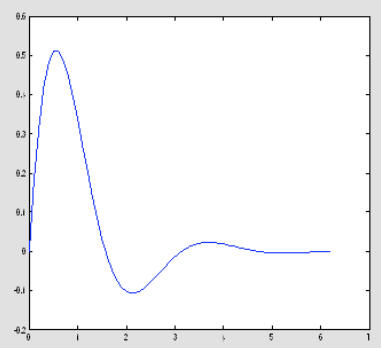
One can plot several curves at the same time
plot(x,y, x,sin(x)) % The two curves appear in distinct colors; both
use the same scale
MATLAB offers many formatting options for such plots, e.g.
x = 0 : 0.1 : 2*pi;
subplot(2,3,1); plot(x,y, x,sin(x)), axis auto
subplot(2,3,2); plot(x,y, x,sin(x)), axis tight
subplot(2,3,3); plot(x,y, x,sin(x)), axis tight, axis off
subplot(2,3,4); plot(x,y, x,sin(x)), axis equal
subplot(2,3,5); plot(x,y, x,sin(x)), axis([0 7 -1 1]), grid on
subplot(2,3,6); plot(x,y,'g.', x,sin(x),'ro'), axis tight, axis square
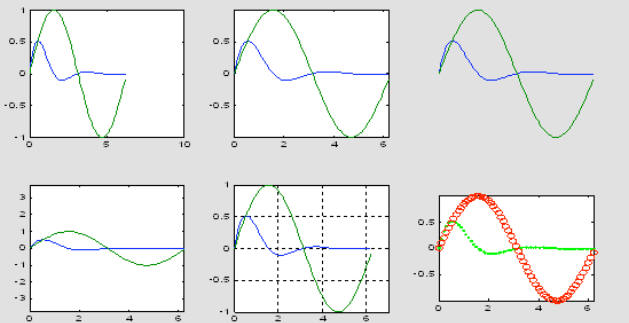
The
command subplot(m,n,p) divides the window into mxn regions (m rows and
n columns) and chooses
the pth plot for drawing into. The numbering of the regions is from left to
right, then
down, as you read text.
There are numerous
plot types for the data marks
"." – point
"+" – plus
"*" – star
"d" – diamond
"o" – circle
"p" – pentagon
"s" – square
"^" – triangle
"x" – x-mark
Line types and line
colors are, among others,
"-" – solid line
"--" – dashed line
":" – dotted line
"-." – dash-dotted line
"r" – red
"y" – yellow
"m" – magenta
"c" – cyan
"g" – green
"b" – blue
"w" – white
"k" – black
A
3D plot is obtained with the command plot3.
t=0:.1:2*pi;
plot3(cos(2*t), sin(2*t),t)
You
can rotate the 3D plot by invoking the command
rotate3d
Simply click the mouse button on the plot and drag. You will change in this way
the viewing
angle.
Releasing the mouse button redraws the data. Type rotate3d again to turn off
this feature.
Operations with figures
figure – opens a new
graphic window , numbered consecutively from the
previous window
figure(n) – makes an
existing graphic window (n) the current window; (all
graphic commands will applythe current window)
pause – holds up
execution of the script until the user presses a key
pause(s) – holds up
the execution of the script for s seconds
close(n) – closes the
graphic window (n)
close all – closes all
graphic windows
clf – clears
everything inside the graphic window
cla clears the plotted
curves and redraws the axes
figure
('Position',[pix,piy,pwx,pwy]) – sets the size and shape of the
current window
o pix,piy – horizontal and vertical cordinates of the left bottom corner of the
window
o pwx, pwy – number of pixels in the width and height of the window
o defalut – figure ('Position',[232,258,560,420])
get ( gcf ) – displays
the properties of the current figure, e.g. size, location, color
map, and many others
set (gcf, 'PropertyName',
PropertyArray) – changes the property
"PropertyName" of the current window
according to the data in PropertyArray, e.g.
set (gcf, 'DefaultTextColor', 'blue')
set (gcf,'PaperPosition',[0.25 2.5 4 3]);
hold on – superposes
several plots on the same graph, even if another script is
executed (default is hold off)
hold off – recommeded
to be used at the end of the script whenever hold on has
been used in the script.
Labels and titles
xlabel('x-axis')
– the string 'x-axis' is printed as a label for the x-coordinate
ylabel('y-axis')
– the string 'y-axis' is printed as a label for the y-coordinate
title("The graph of
y=f(x)') – the string 'The graph of y=f(x)' is printed as
a title of the plot
legend('y=f(x)')
– the string 'y=f(x)' is printed In a small sub-window showing
the line type or data marks
text(x,y,'TextBody')
– the string 'TextBody' is printed on the figure, starting at
the absolute coordinate (x,y) pixels.
Font size
plot(x,y,'-', 'linewidth',3)
– the defalut line width is 0.5
xlabel('x-axis','fontsize',14)
– the default font size is 12pt
| Prev | Next |