Review foe Math Chapter 1

1. Find the input of the function 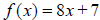corresponding to the output .

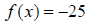2. Find the input of the function 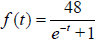corresponding to the output 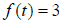to 
three decimal places .

3. Find the slope m and y -intercept b of the line whose equation is given below.

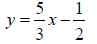
4. Find the rate of change of the function 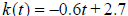million people of age t (in
years).

5. Find the rate of change of the function 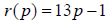thousand dollars when p is
hundreds of units sold.

6. For the function 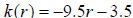, determine if the slope is positive or negative and if
the function is increasing, decreasing, or constant.

7. For the function 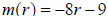, determine the vertical axis intercept.

8. Residential customers who heat their homes with natural gas have their monthly bills
calculated by adding a base service charge of $5.33 per month and an energy charge of
41.89 cents per hundred cubic feet . Write an equation for the monthly charge y (in
dollars) in terms of x , the number of hundreds of cubic feet used.

9. In a study using 50 foreign-language vocabulary words, the learning rate L (in words per
minute) was found to depend on the number of words already learned x, according to the
equation 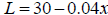. Use the intercepts to determine a window, and then use a
graphing utility to graph the equation for 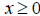Based on the graph, is the learning rate
increasing or decreasing?

10. Graph the function .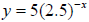

11. Graph the function.



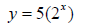
12. Give the constant percentage change of the function

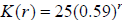
13. Give the constant percentage change for the function .

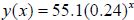14. The monthly sales S for a product is given by 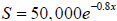, where x is the number of
months that have passed since the end of a promotional campaign. How many months
after the end of the campaign will sales drop below 2000, if no new campaign is
initiated?

15. An initial amount of 250 g of the radioactive isotope thorium-234 decays according to ,
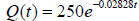,where t is in years. How long does it take for half of the initial
amount to disintegrate? This time is called the half-life of this isotope.

16. The purchasing power P (in dollars) of an annual amount of A dollars after t years of 9%
inflation decays according to 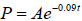. Determine how large a pension A needs to be
so that the purchasing power P is $70,000 after 15 years?

17. The concentration y of a certain drug in the bloodstream t hours after an oral dosage
(with 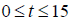) is given by the equation 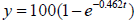. What is the concentration
after 6 hours?

18. The following table gives the percent of the U.S. population with Internet connections
for the years 1997 to 2003. Use a calculator to find the logistic function that models
these data. Use x as the number of years past 1995.

Year
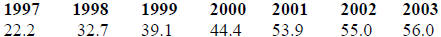Percent with Internet
Source: U.S. Department of Commerce

19. The following table gives the percent of the U.S. population with Internet connections
for the years 1997 to 2003. Use a calculator to find the logistic function that models
these data and then use the model to predict when 58.8% of the U.S. population will
have internet connections. Use x as the number of years past 1995.

Year
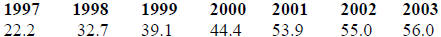Percent with Internet
Source: U.S. Department of Commerce

20. On a college campus of 10,000 students, a single student returned to campus infected by
a disease. The spread of the disease through the student body is given by
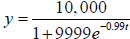, where y is the total number infected at time t (in days). The school
will shut down if 55% of the students are ill. What value of t corresponds to this percentage?

21. In 1996, the population of a country was estimated at 4 million. For any subsequent year
the population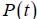 in millions is

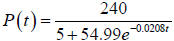
where t is the number of years since 1996. Use a graphing calculator to estimate the
population in 2005.

22. Suppose the table below lists the cumulative number of bases stolen by a baseball player
between 1951 and 1963. Estimate the number of bases this player stole in 1964 by using
a logistic model for the data.

Year	Cumulative stolen bases

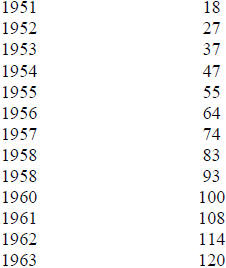23. The table below models a population projection for a certain region for the years after
1800. Use a logistic model to estimate the population in 2047.

Year	Population (millions)	Year	Population (millions)

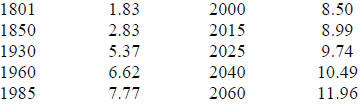24. The sensitivity S to a drug is related to the dosage size by 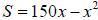, where x is the
dosage size in milliliters. Determine all dosages that yield 0 sensitivity.

25. Choose the function type for the mathematical model that best represents the given data
set.



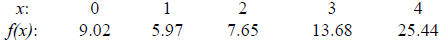
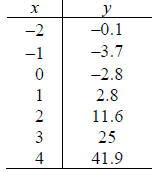
26. Find the equation of the quadratic function that is the best fit for the given data.



27. Suppose that the percent of total personal income that is used to pay personal taxes is
given by ,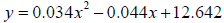
where x is the number of years past 1990 (Source: Bureau of Economic Analysis, U.S.
Department of Commerce). Find the year or years when the percent of total personal
income used to pay personal taxes is 17 percent.

28. If a ball is thrown upward at 128 feet per second from the top of a building that is 70
feet high, the height of the ball can be modeled by
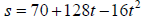, where t is the number of seconds after the ball is thrown. How long
after it is thrown is the height 70 feet?

29. An equation that models the number of users of the Internet is
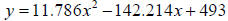million users, where x is the number of years past 1990
(Source: CyberAtlas, 1999). If the pattern indicated by the model remains valid, when
does this model predict there will be 900 million users?

30. Choose the function type for the mathematical model that best represents the given data
set.

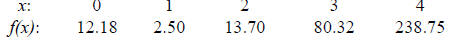
Answer Key



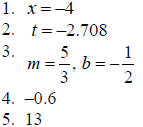
6. slope is negative and function is decreasing


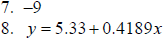
9. decreasing
.
12. –41%
13. –76.0%
14. 4.02 months
15. 24.5 years
16. $270,020
17. 93.7
18.

19. 2006
20. 9.51
21. 4,743,000
22. 5
23. 10.84 million
24. x=0 milliliters,  x=150 milliliters
25. quadratic
26. 
27. 2002
28. t=8 seconds
29. 2005
30. cubic