Review of MATH 300

XIV. Old theorems:

A. Division Algorithm : If a and b are positive integers with b less than or equal
to a, then there exists a natural number q and a non - negative integer r such
that a = bq + r, where 0 is less than or equal to r, and r is less than b.
B. Euclid’s Algorithm: Let a and b be two positive integers with b less than or
equal to a. Let d be GCD(b,a). Then:
1. Part 1: You can successively apply the division algorithm to a and b to
find a final remainder r such that r = d
2. Part 2: The GCD of a and b may be written as a combination of a and
b , i.e., d = ax + by for some integers x and y
C. The Fundamental Theorem of Arithmetic : Every natural number can be
expressed uniquely as a product of primes

Assorted Proof Outlines:

XV. Proof that the square root of a prime number p is irrational:

A. Assume that the square root of the p is rational , and rewrite as a fraction of
integers
B. Square both sides, and remove denominator
C. Make a set consisting of all natural numbers which, when multiplied by p ,
equal an integer squared.
D. Show that it is not empty
E. Apply WOP to get a natural number, which, when multiplied by p, yields the
square of an integer
F. Show that p divides that integer squared
G. Subproof: Prove that p divides that integer (not squared)
1. Assume p does not divide it
2. So the GCD of p and that integer is 1
3. Use Euclid’s Algorithm
4. Arrive at the fact that p does divide that integer
5. So p does not divide it implies that p does divide it, i.e., p divides it or
p divides it, i.e., p divides it
H. Apply definition of “divides”
I. Square this, and in doing so, find a new element of the set
J. Show that this element is smaller than the previous smallest element.
K. This is a contradiction, so the square root of p is not rational.

XVI. Proof that every natural number has a prime factor :

A. Let n be an arbitrary natural number
B. Make a set S of all numbers that divide it
C. n is in this set, so it is not empty, so you can apply the WOP to get S’s
smallest member p
D. suppose p is not prime
E. then p has a factor
F. show that there is another natural number, p`, which is in S but smaller than p
G. this is a contradiction, so p is prime
H. so every natural number has a prime factor

XVII. Proof that there are infinite primes:

A. Let 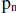, denote a prime number
B. Assume that there are a finite number of primes
C. So, 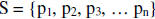, where n is some natural number, is the set of all
prime numbers
D. Let 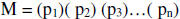and let m = M+1. So m – M = 1
E. Every natural number greater than 1 has a prime factor
F. So m is divisible by some prime number q
G. Suppose q is an element of S. So q/M. But q/m. m – M = 1. Show that q
divides 1.
H. So t = 1/q for some integer t
I. Arrive at a contradiction (0 = 1)
J. So q is not an element of S
K. So q is a prime number but q is not a member of the set of all prime numbers
L. This is a contradiction, so the set of primes is infinite

Functions:

XVIII. Functions in general:

A. Function: A function f from A to B is a relation f from A to B such that:

1. For every x∈A there is a y∈B such that xfy
2. For every x∈A, if xfy and xfz, then y = z

B. If f is a function from A to B, we write f:A→B

C. If f:A→B and a∈A, then we write f(a) for the unique b∈B such that (a,b)∈f;

i.e., instead of (a,b)∈f, we write f(a) = b

D. Restriction: if f is function from A to B and S is a subset of A, we can define a
function f/S by letting f/S = the intersection of f and the Cartesian Product of
S and B; i.e., f/S = {(x,y)∈f: x is an element of S}

E. One-to-one: let f be a function from A to B. we say that f is one-to-one iff f(x)
= f(y) implies x = y

F. Onto: let f be a function from A to B. f is onto B iff for every b∈B, there is an
a∈A such that f(a) = b

G. Bijection: Let A and B be sets. A bijection from A to B is a function f:A→B
which is one-to-one and onto

H. Equivalent: Two sets A, B are equivalent iff there exists a bijection from A to
B, and we write A ≈ B.

XIX. Special Properties of Functions (easy to prove):

A. The composite of two functions is a function
B. The composite of two onto functions is onto
C. The composite of two one-to-one functions is one-to-one
D. The composite of two bijections is a bijection
E. The inverse of a function f is a function iff f is a bijection
F. ≈ is an equivalence relation

Cardinality

XX. Cardinality in General:

A. 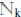: If k∈N, then 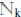= {n∈ N: n ≤ k}
B. Finite: A set S is finite iff S = Ø or S ≈ 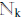for some k∈ N.
C. Infinite: A set S is infinite iff it is not finite
D. Cardinal number: Let S be a finite set. If S ≈ 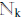for some k∈ N, then S has
cardinal number k, or cardinality k. If S = Ø then we say that S has cardinal
number 0, or cardinality 0.
E. Denumerable: Let S be a set. S is denumerable iff S ≈ N. For a denumerable
set S, we say S has cardinal number 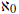or cardinality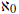
F. Countable: A set S is countable iff it is finite or denumerable
G. Uncountable: A set S is uncountable iff it is not countable

XXI. Special Properties of Cardinality (proved later):

A. The cardinality of a finite set is unique
B. A finite set is not equivalent to any of its proper subsets
C. Every subset of a finite set is finite
D. Every proper subset of a finite set has smaller cardinality
E. The union of two finite sets is finite

Consequences of Functions and Cardinality:

XXII. Pigeon Hole Principle: for every n∈N, if r∈N and n > r and 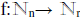, then f is
not one-to-one

A. Lemma for proving the Pigeon Hole Principle: If r ∈N and r > 1 and x ∈,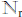
then .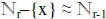

B. Proving Pigeon Hole Principle:
1. Use induction on “if r∈N and n > r and 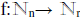, then f is not one-to-
one” starting with n = 2
2. P(2) is true because if f:{1,2}→{1}, then f(1) = 1 and f(2) = 1, so f(1)
= f(2) but 1 ≠ 2, so f is not one-to-one
3. Assume P(n) for arbitrary n∈ N
4. Suppose r∈N and n+1 > r and F: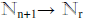
5. Suppose F is one-to-one
6. Let g be the restriction of F to .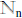
7. So g: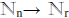
8. Let x∈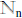 be arbitrary
9. Suppose g(x) = F(n+1). Get a contradiction because then F(x) =
F(n+1), but x ≠ n+1, so F is not one-to-one
10. So g(x) ≠ F(n+1) for any x∈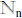
11. So g: 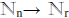– {F(n+1)}
12. Suppose g is not one-to-one. Then there exist a,b∈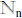 such that g(a) =
g(b) and a ≠ b. Get a contradiction because F is not one-to-one.
13. So g is one-to-one
14. By the Lemma, – {F(n+1)} ≈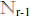
15. So there exists a bijection h: – {F(n+1)}→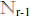
16. So
17. Since g is one-to-one and h is one-to-one, 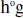is one-to-one
18. Since r < n+1, r-1<n
19. So 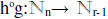and r-1<n, which contradicts the hypothesis of
induction
20. So F is not one-to-one. So r∈N and n+1 > r and F: imply F
is not one-to-one. So for every r, r∈N and n+1 > r and F:
imply F is not one-to-one, i.e., P(n+1).
21. Finish out PMI proof

XXIII. Proof Outlines for Special Properties of Cardinality:

A. Proving that the cardinality of a finite set is unique:
1. Make an arbitrary set with cardinality k and cardinality m
2. Suppose k ≠ m. So one is larger. Pick k to be larger.
3. Show that there is a bijection from to
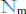
4. The Pigeon Hole Principle says this is impossible
5. So k = m

B. Proving that a finite set is not equivalent to any of its proper subsets:

1. Let A be an arbitrary finite set and let B be a proper subset of A
2. So A ≈ for some k∈N or A = Ø, and B is a subset of A, and B ≠ A
3. Suppose A = Ø. So A has no elements, so B does not exist. So ~A ≈ B
4. Suppose A ≈ for arbitrary k∈N. From B ≠ A and B is a subset of
A, show that A is not a subset of B
5. So there is an x that is in A but not in B
6. Make a bijection f:A→ and make g its restriction to B
7. Show by contradiction that g(b) ≠ f(x) for any x
8. So g:B→–{f(x)}
9. Apply Lemma to show that –{f(x)} ≈
10. Use it to make a bijection h
11. So there is now (by composite) a bijection from B to
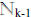
12. So B ≈ 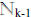, but ~ ≈ 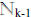because the Pigeon Hole Principle says
that this is impossible. So ~B ≈ A.

C. Proving that any subset of a finite set is finite:

1. Let A be an arbitrary finite set. So A ≈ for some k∈ N or A = Ø.
2. Let B be a subset of A
3. Suppose A = Ø. Then B = Ø, so B is finite
4. Suppose A ≈ for some k∈ N
5. Then there is a bijection f:A→
6. Suppose A = B. Then g:B→ is a bijection. So B ≈ . So B is
finite.
7. Suppose A ≠ B. Then there is an x in A but not in B.
8. Let h be the restriction of f to B
9. Show that h(b) ≠ f(x) for any b∈B
10. So h:B→ -{f(x)}
11. Show that h is one-to-one and onto by contradiction
12. So h is a bijection and B ≈ -{f(x)}
13. By the Lemma, B ≈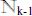
14. So B is finite
15. So in all cases, B is finite, and so any subset of a finite set is finite

XXIV. Other Assorted Proofs:

A. Proving that N is infinite:
1. Suppose N is finite
2. Then N ≈ for some k∈ or N = Ø
3. N ≠ Ø because 1∈ N
4. So N ≈ for some k∈
5. So there exists a bijection f:→N
6. Let n = f(1) + f(2) + … + f(k) + 1
7. Then n∈N but ~n∈ because n is larger than any element of
8. So f is not onto. But f is onto because it is a bijection. This is a
contradiction. So N is not finite. So N is infinite.

B. Proving that (0,1) is uncountable:
1. Suppose (0,1) is finite
2. Then (0,1) ≈ for some k∈N or (0,1) ≈ Ø
3. (0,1) ≈ Ø because 0.5∈(0,1)
4. So (0,1) ≈ for some k∈N
5. So there exists a bijection f:→(0,1)
6. Let a be the largest of f(1), f(2), f(3), … f(k)
7. Let b = (a+1)/2. Then b∈(0,1) but f(j) ≠ b for any j∈ because b >
the greatest f (k)
8. So f is not onto, contradicting the fact that f is a bijection.
9. So (0,1) is infinite
10. Suppose (0,1) is denumerable
11. So N ≈ (0,1)
12. So there exists a bijection g: N→(0,1)
13. So f(1) =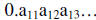
(i) f(2) =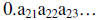
(ii) f(3) =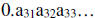
14. etc, where 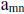∈{0,1,2,3,4,5,6,7,8,9} and all decimals are in
normalized form
15. let b = 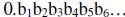where 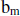= 5, if 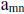≠ 5 and 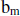= 3, if 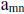= 3
16. then b∈(0,1) but b ≠ f(j) for any j∈N, so f is not onto, contradicting
the fact that f is a bijection. So (0,1) is not denumerable
17. Since (0,1) is not finite or denumerable, it is uncountable