Sample Algebra Test Questions
Chapter 1 Basic Algebra Operations
1-1 algebra and real numbers
1. Perform the indicated operations on each of the following and write the
result as simply as
possible:
2. Classify each of the following values into one or more
of the sets —list all the sets each
belongs to:
N natural numbers
Z integers
Q rationals
R reals
3. The number sets are:
N natural numbers
Z integers
Q rationals
R reals
a. addition
(3)
b. subtraction
(3)
c. division
(3)
d. multiplication
3)
e. square root of a positive number
(3)
1-2 polynomials : basic operations
4. Perform the indicated operations and simplify:
a. (x2−3x+1) + (x3−4)
(10)
b. (x2−3x+1) − (x3+10)
(10)
c. (x−2)•(x2+3x−1) − (x3+10)
(10)
d. (x+2)(x−3)
(10)
e. (x2+3)(x+5)
(10)
f. (x+2)•(x2−3x+1) − (x3+7)
(10)
1-3 polynomials: factoring
5. What are the prime factors of each of the following ? If the value is prime,
then write PRIME.
a. 42
(2)
b. 180
(3)
c. 89
(2)
d. 1540
(3)
e. 360
(2)
f. 666
3)
6. Factor completely relative to the integers. If the
expression cannot be factored, the write
PRIME.
a. 2x3 − 8x2 + 10x
(10)
b. 48a8x − 75b2x3
(10)
c. 4x4 − 28x3 + 48x2
(10)
d. 3x2 − 15x + 18
(10)
e. 16a4x3 + 36b8x
(10)
f. 12a2x3 − 27b6x
(10)
g. 2x2 + 2x − 12
(10)
1-4 rational expressions: basic operations
7. Reduce the fraction to lowest terms:
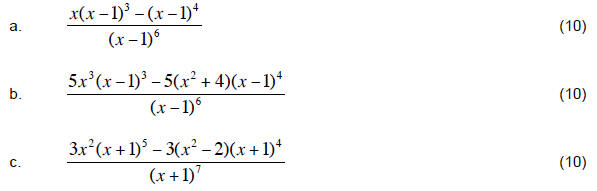
8. Simplify:
9. Express as a simple fraction reduced to lowest terms :
1-5 integer exponents
10. Perform the indicated operation (division) and simplify:
1-6 rational exponents
11. Simplify using positive exponents only :
1-7 radicals
12. Simplify:
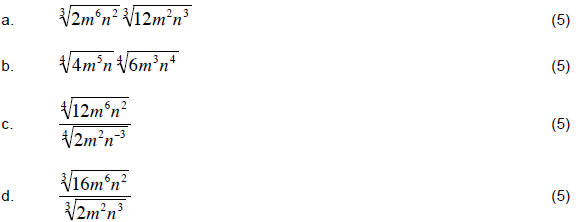
| Prev | Next |