Reducing Rational Functions

Sign Changes

It is not uncommon that you will have to manipulate the signs in a fraction in order to
obtain common factors that can be then cancelled . Consider, for example, the rational
expression

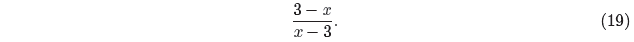
One possible approach is to factor −1 out of the numerator to obtain

You can now cancel common factors.

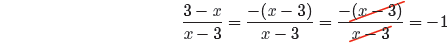
This result is valid for all values of x , provided x ≠ 3.

Let’s look at another example.

Example 20. Reduce the rational expression

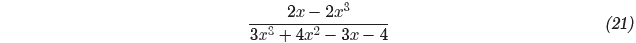
to lowest terms . State all restrictions.

In the numerator, factor out 2x, then complete the factorization using the difference
of two squares pattern.

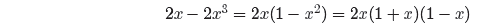
The denominator can be factored by grouping.

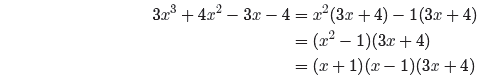
Note how the difference of two squares pattern was applied in the last step.

At this point,

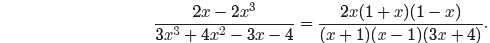
Because we have 1 − x in the numerator and x − 1 in the denominator, we will factor
out a −1 from 1−x, and because the order of factors does not affect their product, we
will move the −1 out to the front of the numerator.

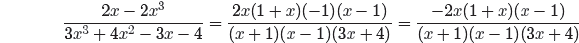
We can now cancel common factors.

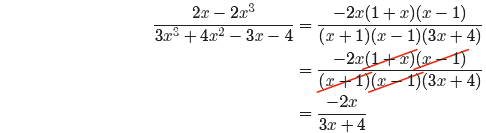
Note that x + 1 is identical to 1 + x and cancels. Thus,

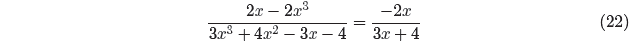
for all values of x, provided x ≠ −1, 1, or −4/3. These are the restrictions, values of x
that make denominators equal to zero.

The Sign Change Rule for Fractions

Let’s look at an alternative approach to the last example. First, let’s share the precept
that every fraction has three signs, one on the numerator, one on the denominator, and
a third on the fraction bar. Thus,

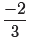has understood signs .

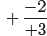Let’s state the sign change rule for fractions .

For example, let’s start with −2/3, then do two negations: numerator and fraction
bar. Then,

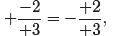or with understood plus signs, .

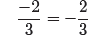This is a familiar result, as negative two divided by a positive three equals a negative
two-thirds.

On another note, we might decide to negate numerator and denominator. Then
−2/3 becomes

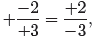, or with understood plus signs, .

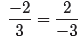Again, a familiar result. Certainly, negative two divided by positive three is the same
as positive two divided by negative three. They both equal minus two-thirds.

So there you have it. Negate any two parts of a fraction and it remains unchanged.
On the surface, this seems a trivial remark, but it can be put to good use when reducing
rational expressions. Suppose, for example, that we take the original rational expression
from Example 20 and negate the numerator and fraction bar.

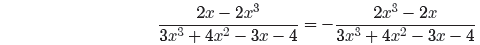
Note how we’ve made two sign changes. We’ve negated the fraction bar, we’ve negated
the numerator (−(2x − 2x³) = 2x³ − 2x), and left the denominator alone. Therefore,
the fraction is unchanged according to our sign change rule.

Now, factor and cancel common factors (we leave the steps for our readers —they’re
similar to those we took in Example 20).

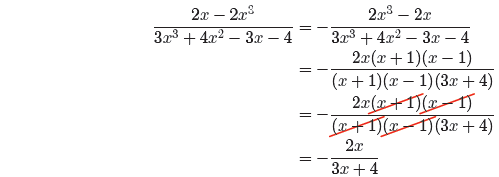
But does this answer match the answer in equation (22)? It does, as can be seen by
making two negations, fraction bar and numerator.

The Secant Line

Consider the graph of the function f that we’ve drawn in Figure 3. Note that we’ve
chosen two points on the graph of f, namely (a, f(a)) and (x, f(x)), and we’ve drawn
a line L through them that mathematicians call the “secant line.”

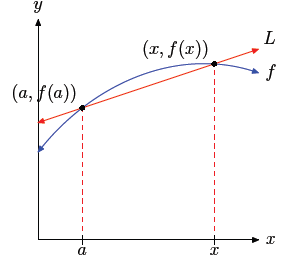
Figure 3. The secant line passes through
(a, f(a)) and (x, f(x)).

The slope of the secant line L is found by dividing the change in y by the change in x.

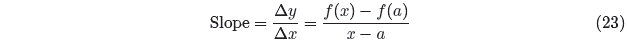
This slope provides the average rate of change of the variable y with respect to
the variable x. Students in calculus use this “average rate of change” to develop the
notion of “instantaneous rate of change.” However, we’ll leave that task for the calculus
students and concentrate on the challenge of simplifying the expression equation (23)
for the average rate of change.

Example 24. Given the function f(x) = x², simplify the expression for the
average rate of change, namely

First, note that f(x) = x² and f(a) = a², so we can write

We can now use the difference of two squares pattern to factor the numerator and
cancel common factors.

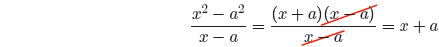
Thus,

provided, of course, that x ≠ a.

Let’s look at another example.

Example 25. Consider the function f(x) = x² − 3x − 5. Simplify

First, f(x) = x²−3x−5 and therefore f(2) = (2)²−3(2)−5 = −7, so we can write

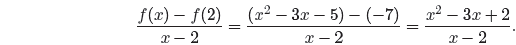
We can now factor the numerator and cancel common factors.

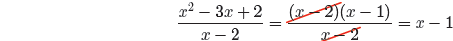
Thus,

provided, of course, that x ≠ 2.