SOLVING SYSTEMS OF EQUATIONS
GRAPHING SYSTEMS OF EQUATIONS – INVESTIGATION WORKSHEET
Veronica is considering two job offers in car sales. The first job pays $400 per
week plus
15% sales commission. The second job pays $350 per week plus 20% sales
commission.
What amount would Veronica have to sell for her weekly salary to be the same at
either
job?
Problems:
1. Write two equations, one for each job, representing the amount of
weekly sales, x,
and total weekly salary, y.
2. Type these two equations into Y1 and Y2 in the graphing calculator. Graph the
functions. What is on the screen? How does the viewing window need to be
adjusted?
3. Find the point of intersection of the two lines. What is the ordered pair ?
4. At what amount of sales will the two jobs have the same salary? What will
that
salary be?
Solution – 2. xmax – 1200, ymax – 700 3. (1000, 550) 4. Sales $1000, Salary $550
Solving Systems of Equations
Elimination by Addition & Subtraction
Solve the following systems of equations using elimination by addition or
subtraction .
1.
2x+8y =2
-2x-4y=6
2.
a+b=11
a-b=4
3.
2x-3y=5
5x-3y=11
4.
2m+n=-5
2m+3n=7
5. Suppose two eggs with bacon cost $2.70. One egg with bacon costs $1.80. At
these rates, what will bacon alone cost?
6. Five gallons of regular unleaded gas and eight gallons of premium gas cost
$17.15. Five gallons of regular unleaded and two gallons of premium gas cost
$8.75. Find the cost per gallon of each kind of gasoline.
Answers – Solving Systems of Equations using Elimination
by addition &
subtraction.
1. x=-7 y=2
2. a=7.5 b=3.5
3. x=2 y=-1/3
4. m=-5.5 n=6
5. eggs=.90 bacon=.90
6. regular = 1.19 premium=1.40
Systems of Equations
Matrices
Use the graphing calculator to solve the following systems of equations using
matrices.
Show your work and the key sequence of the calculator steps for full credit!
1.
2x+3y=15
5x-2y=-29
2.
5x=4y+15
6y=3x-9
3. The sum of two numbers is 45. Three times the first number plus seven times
the
second is 115. Find the two numbers.
4. Tickets for a school play sell for $3 for a student and $5 for an adult. One
night 595
people bought tickets. The school took in $1951. How many adult tickets and how
many
student tickets were sold?
5. Mary has 30 nickels and dimes totaling $2.40. How many of each does she have?
ANSWERS – Systems of Equations using Matrices
1. x=-3, y=7
2. 5x-4y=15, -3x+6y=-9; x=3, y=0
3. x+y=45, 3x+7y=115; x=50, y=-5
4. s+a=595, 3s+5a=1951; s=512, a=83
5. n+d=30, 5n+10d=240; n=12, d=18
Systems of Equations Quiz
1. Graph the system of equations. Then determine whether the system has no
solution,
one solution, or infinitely many solutions. If the system has one solution, name
it.
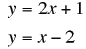
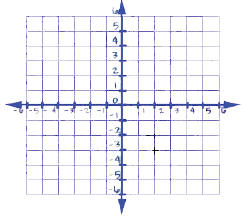
Use substitution to solve the system of equations.
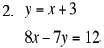
Use elimination to solve the system of equations.
4. At a local electronics store, CDs were on sale. Some
were priced at $14.00 and some at
$12.00. Sabrina bought 9 CDs and spent a total of $114.00. How many $12.00 CDs
did
she purchase?
Systems of Equations
Answer Section
SHORT ANSWER
1. ANS:
one solution; (–3, –5)
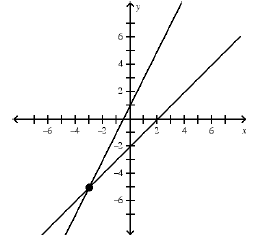
Graph each line. The point where the two lines intersect
is the solution. Check the
solution by replacing x and y in the original equations with the values in the
ordered pair.
DIF: Average OBJ: 7-1.2 Solve systems of equations by graphing.
STO: A.A.7, A.G.7  TOP: Solve systems of
equations by
TOP: Solve systems of
equations by
graphing
KEY: System of Equations, Graphing MSC: 1998 Lesson 8-1
NOT: /A/ Remember that the x-coordinate comes first in an ordered pair. /B/ Did
you
graph the second line correctly? /C/ Graph both lines./D/ Correct!
2. ANS:
(33, 36)
Substitute the right side of the top equation for y in the bottom equation.
Solve for x.
Substitute the value obtained for x into the top equation and solve for y.
DIF: Average OBJ: 7-2.1 Solve systems of equations by using substitution.
STO: A.A.7, A.A.10, A.G.7
TOP: Solve systems of equations by using substitution
KEY: System of Equations, Substitution MSC: 1998 Lesson 8-2
NOT: /A/ Remember to list the x-coordinate first and then the y-coordinate./B/
Use
parentheses when you sustitute for y and then remember to distribute the
negative sign
through the parentheses. /C/ Terms with different variables cannot be combined.
/D/
Correct!
3. ANS:
(–1, –1)
Eliminate one variable by adding the two equations . Solve for x and then
substitute that
value into one of the equations to find the value of y.
DIF: Average OBJ: 7-3.1 Solve systems of equations by using elimination with
addition.
STO: A.A.7, A.A.10, A.G.7
TOP: Solve systems of equations by using elimination with addition
KEY: System of Equations, Elimination, Addition
 MSC: 1998 Lesson 8-
MSC: 1998 Lesson 8-
3
NOT: /A/ Correct! /B/ Double-check your positive and negative signs . /C/ Add the
equations together./D/ Add the equations together.
4. ANS:
6
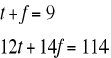
Solve the first equation for one of the variables and substitute into the second
equation.
Solve. Substitute that value into the first equation to find the second value.
DIF: Average OBJ: 7-2.2 Solve real-world problems involving systems of
equations.
STO: A.A.7, A.A.10, A.G.7
TOP: Solve real-world problems involving systems of equations
KEY: System of Equations, Real-World Problems  MSC:
1998 Lesson 8-
MSC:
1998 Lesson 8-
2
NOT: /A/ This is the total number of CDs purchased. /B/ Correct! /C/ Does your
answer
satisfy the equations? /D/ This is the number of $14.00 CDs purchased.



System of Linear equation
|
Find an (x,y) value that makes both equations true. Warning !There are three tricky ones! If both equations represent exactly the same line , then ALL real numbered ordered. pair will work. If the equations represent two parallel lines ,NO real numbers will work since the lines will not interest. |
 |
Please show all of your work on this worksheet.

| Prev | Next |