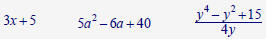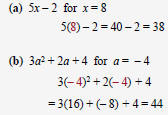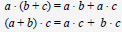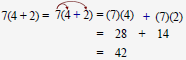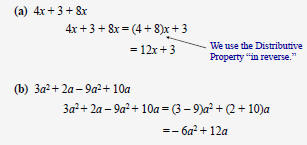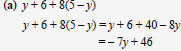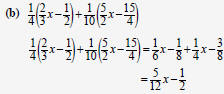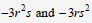Simplifying Algebraic Expressions

Algebraic Expressions

Algebra is a branch of mathematics in which symbols represent
numbers or members of a set.

A variable is a letter used to represent any number.

A constant is either a fixed number or a letter that represents a
fixed number.

An algebraic expression is any combination of variables,
constants, grouping symbols , and mathematical operations.

Evaluating Algebraic Expressions

To evaluate an algebraic expression, substitute the numerical
value for each variable into the expression and simplify the
result .

Example:
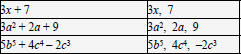
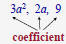
Evaluate each expression for the given value.

Like Terms

A term is a constant or the product or quotient of a constant
and one or more variables raised to powers .

Algebraic Expression	Terms

Terms that have the same variable factor (s) with the same
exponent (s) are called like terms.

The Distributive Property

The Distributive Property
If a, b, and c are real numbers , then

That is, multiply each term inside the parentheses by the factor
on the outside.

Example: Use the Distributive Property to remove the parentheses.

Combining Like Terms

Example:
Simplify each expression by combining like terms.

Combining Like Terms

Example:
Simplify each expression.


	Distribute.
	Combine like terms

	Distribute.
	Combine like terms.

Practice

Evaluate each expression using the given values of
the variable(s).

Practice

Determine if the terms are like or unlike

Practice

Use the distributive property to remove the
parentheses .

Practice

Simplify each expression by combining like terms