Some Second Degree & Trig Curves

THE UNIVERSITY OF AKRON
Mathematics and Computer Science

Table of Contents
 

10. Some Second Degree & Trig Curves
10.1. Parabolas
• x is of second degree • y is of second degree • Intersecting
Curves
10.2. Circles
10.3. The Trig Functions
• The Definitions and Consequences • Some Common Values
• Graphs of the Trig Functions • The Other Trig Functions
• Radian Measure versus Degree Measure

In Lesson 9 we gave an extensive discussion of first degree curves;
these are equations having a straight line as its graph. In this lesson,
we begin by exploring selected second degree curves followed by a brief
survey remarks on trigonometric functions.

The general form of a second degree equation is

Ax² + Bxy + Cy² + Dx + Ey + F = 0 (1)

where either A ≠0 or B ≠0. In our lesson, B = 0¹, so, in fact we
will look at equations of the form

Ax² + Cy² + Dx + Ey + F = 0 (2)

The graph of such an equation may be a parabola, a hyperbola , a
circle, or an ellipse (or a degenerate graph). We discuss only parabolas
and circles leaving the others to a (high school) course in Analytic
Geometry, a course in Precalculus, or a course in Calculus and
Analytic Geometry.

Associated with any second degree equation (equation (2)) is a ver y
strong geometry. For example, a parabola has a focus and the parabola
has a certain reflection property that is exploited in the manufacture
of flash lights, satellite dishes, parabolic mirrors, etc. These geometric
properties will not be covered in these lessons; again they are a topic
of study in a course on Analytic Geometry. Instead, we will concentrate
on the mechanics: recognition, classification, location, and
graphing.

10.1. Parabolas

A parabola is described by a second degree equation (in the variables
x and y) in which one variable has power two and the other variable
has power one. (In terms of equation (2), this means A = 0 or C = 0,
but not both.)

It is important to be able to recognize second degree equations whose
graph is a parabola. Study the following examples to acquire an “eye.”

Illustration 1. Parabolas.

(a) The x variable has degree 2 and the y variable has degree 1. In
this case y is expressible as a function of x.
1. Equational Form:

x² − x + y = 1
3x² − 2x + 3y = 5
y − x + 5x² = 0

2. Explicit Form: y written (explicitly) as a function of x:

y = x²
y = 1− x² +x
y= 1/3(5x² + 2x)

(b) The y variable has degree 2 and the x variable has degree 1. In
this case x is expressible as a function of y.
1. Equational Form:

x + y + y² = 5
3x − 6y² + y − 8 = 0
y² = 2x + 3y

2. Explicit Form: x written (explicitly) as a function of y.
x = y²
x = 2y² − 5y +1/2
x = 4y² + 7y − 1

• x is of second degree
An equation in which the x variable has the second degree and the
y variable has the first degree is a parabola that either opens up or
opens down.

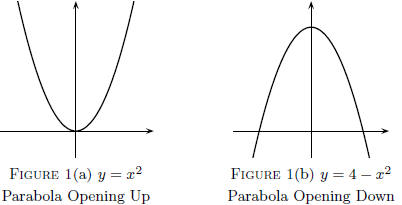
Notice that these two parabolas pass the vertical line test; this means
that each defines y as a function of x. (The equations are y = x² and
y = 4 − x².) A parabola has a vertex that represents the absolute
minimum, see Figure 1(a), or the absolute maximum, Figure 1(b),
of the graph.

The skills associated with working with parabolas are as follows:
• Recognition: Recognize the equation as a parabola of this
type.
• Classification: Classify the parabola as one that opens up or
one that opens down.
• Location: The parabola is located by calculating its so-called
vertex.
• Graphing: If needed, we need to graph the parabola.

Recognition. We’ve already covered the case for recognition. The
important point is that the variable x as degree two and the variable
y has degree one.

We shall satisfy ourselves by just presenting a quiz. Passing is 100%
so don’t err!

• Quiz. Click on the green bullet to jump to the quiz on parabolas.

Classification. The general form of a parabola that can be written
as a function of x is

y = ax² + bx + c, a ≠ 0  (3)

We state the following without proof, though the validity of the statements
will be made apparent later.
 

Classification Rule : Consider the parabola y = ax2 + bx + c, a ≠ 0  . (4) The parabola opens up if a > 0 and opens down if a < 0; i.e., if the coefficient of the second degree term is positive, the parabola opens up, and opens down if the coefficient of the second degree term is negative.

Naturally, you must strive to put your equation in the form of (4)
before you can make the correct determination.

This is such a simple principle , let’s just quiz you on it.
• Quiz. Click on the green bullet to jump to the quiz on parabolas.
Location. A parabola that is a function of x has the form

y = ax² + bx + c, a ≠ 0. (5)

Such a parabola opens up (if a > 0) or down (if a < 0). Another
important feature of a parabola is the presence of a vertex. The vertex
of the parabola in equation (5) can be determined by completing the
square of the right -hand side.

Generally, when you complete the square of (5), you obtain an equation
of the form

y − k = a(x − h)², (6)

where h and k are constants. It turns out that the vertex is located
at coordinates V ( h, k ).

Example 10.1. Find the vertex of the parabola y = x² − 2x + 4.

The previous example was surely of Skill Level 0; the completion
of the square was no problem. In the next example, the completion
process is slightly trickier.

Example 10.2. Find the vertex of the parabola 4x² + 3x + 2y = 3.

Before asking you to do a few, let’s summarize.

Finding the Vertex : Given a second degree equation that has been put into the form y = ax2 + bx + c, a ≠ 0, the vertex can be obtained by completing the square. This having been done, put the equation into standard form: y − k = a(x − h)2  (7) The vertex is located at V ( h, k ).

Now, let’s go to the exercises. The solutions are on separate pages.
You can look at them in order without seeing the solution to the next
one. Use this to refine you solution methods.

Exercise 10.1. (Skill Level 0) Use the technique of completing the
square to put each of the parabolas into standard form. Having done
that, write the coordinates of the vertex in the form V ( h, k ) and state
whether the parabola opens up or down.

(a) y = x² − 6x
(b) y = 1− 4x − x²
(c) x² + 2x + y+1 = 0

In the next exercise the problem of completing the square is a little
trickier, but I expect you will get a score of 100%.

Exercise 10.2. (Skill Level 0.5) Use the technique of completing the
square to put each of the parabolas into standard form. Having done
that, write the coordinates of the vertex in the form V ( h, k ) and state
whether the parabola opens up or down.

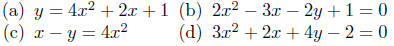
We now turn to the topic of graphing.

Graphing.

Graphing a parabola is very simple once you have obtained some basic
information about the parabola:

• Orientation. Does the parabola open up/down, or right/left.
This information can be easily observed using the classification
rules.

• Location. The vertex determines the location of the parabola.
See the discussion on finding the vertex.

Other points of interest in graphing a parabola are

• Symmetry. A parabola that is vertically oriented—it opens up or
down—is symmetrical with respect to the vertical line passing
through the vertex. This makes it even easier to graph.

• Points to Plot. It is not necessary to plot a large number of
points to make a rough sketch. Usually, plotting the vertex, and
two other points to determine the “breath” of the parabola are

sufficient. If the parabola crosses the x-axis, then fixing these
point(s) is useful too.

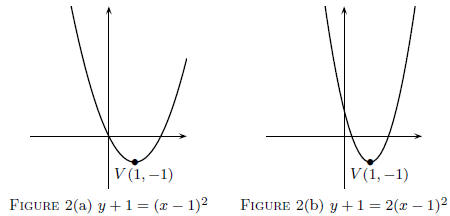
These two parabolas have virtually the same equation; the only difference
is in Figure 2(b), the (x − 1)² is multiplied by 2. This “scaling
factor” tends to narrow the parabola. The get a feel for the breadth of
the parabola, simply plot two points symmetrically placed on either
side of the vertex. The pass a parabolic curve through these three
points. Three points and you’re done!

Exercise 10.3. Find the x- intercepts for the two parabolas in Figure
2:
(a) y+1 = (x − 1)²
(b) y+1 = 2(x − 1)².

Exercise 10.4. Make a rough sketch of each of the following parabolas
on the same sheet of paper.
(a) y = x² + 1
(b) y = 2x² + 1


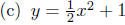
Exercise 10.5. Make rough sketches of the graphs of each of the following
by putting each into standard form; classifying each as opening
up or down; and finding the vertex of each.
(a) 4x + y − x² = 1
 (b) y = −x² − 6x + 1
(c) 2x − 3y = x²

• y is of second degree
When you have a second degree equation, like equation (2), and y has
degree two with x only degree one (A = 0 and C
= 0), you have a
parabola that opens either to the left or to the right. Here are a few
visuals.

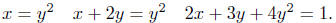
As in the previous case, to analyze these equations the basic skills we
must master the basic skills: recognition, classifcation, location,
and graphing.

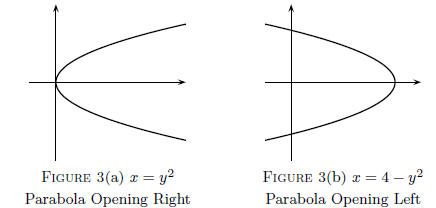
Notice the vertex is the point that is the right-most or left-most point
on the graph, depending on the orientation of the parabola.

Because of the similarity of these case with the previous (extensively
discussed) case, only exercises will be presented. In each exercise, observe
that the parabolas are of the advertised type and that they
equation define x as a function of y.

The general form of a parabola that opens to the left or right, written
as a function of y, is

x = ay² + by + c

Here is all the relevant information.

Analyzing Horizontally Oriented Parabolas: Considerthe parabola x = ay2 + by + c, a ≠ 0. (8) The parabola opens right if a > 0 and opens left if a < 0; This equation can be put into the standard form x − h = a(y − k)2  (9) using the method of completing the square. The location of the vertex is V ( h, k ).

Exercise 10.6. Analyze the following parabolas by putting each
equation into standard form, equation (9), observing its orientation,
finding its vertex, and, finally, making a rough sketch of the
parabola. (The solutions to each are given on separate pages so you
can, for example, look at the solution to (a) to refine your techniques
to solve (b)–(d).)

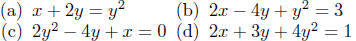
• Intersecting Curves
Quiz. Let y = mx + b and y = ax² + bx + c be a line and a parabola,
respectively. What is the largest number of points of intersection possible
between these two curves?

(a) 0 (b) 1 (c) 2 (d) 3

Let’s have a few “reminder” exercises in the form of solving equations .
Try to graphically visualize the questions; the graphing fanatic might
even graph all these equations . . . perhaps using a graphing calculator.

Exercise 10.7. Find the coordinates of intersection between the two
given curves. (Recall : The Quadratic Formula.)

(a) Write out the general strategy of solving these problems.

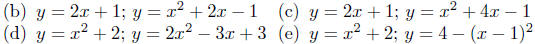
10.2. Circles

 

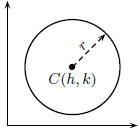
Let r > 0 be a number greater than zero and C( h, k )
a point in the plane. The circle with center at
C( h, k ) and radius r is the set of all points P( x, y )
that are a distance of r units from the point C. In
terms of symbols, a point P is on this circle if (and
only if) it satisfies the equation

d( P,C ) = r, (10)

where d( P,C ) is the distance between the points P and C.

Now, invoke the distance formula with P ( x, y ) and C( h, k ) to obtain

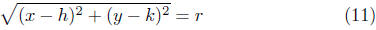
Square both sides to obtain the center-radius form for the equation
of a circle

(x − h)² + (y − k)² = r²

Center-Radius Form of a Circle The equation of the circle having radius r > 0 and center at C( h, k ) is given by (x − h)2 + (y − k)2 = r2   (12)

Illustration 2. Here are a few simple examples of circles already in
the center-radius form; in this case, basic information can be extracted
about the circle.

(a) x² + y² = 1 is a circle of radius r = 1 with center at ( 0, 0 ).
(b) (x − 1)² + (y − 3)² = 16 is a circle with radius r = 4 (r2 = 16)
and center at C( 1, 3 ).
(c) (x + 2)² + (y − 4)² = 5 is a circle with radius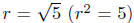
and center at C(−2, 4).

To construct the equation of a circle, therefore, you need two pieces
of information: (1) the center of the circle and (2) the radius of the
circle. All your efforts must be concentrated towards acquiring these
two.

Exercise 10.8. Find the equation of the circle with center at C and
passes through the given point P
(a) Write out a strategy for solving this type of problem.
(b) C( 1, 2 ); P( 4,−1 ) (c) C(−2, 3 ); P( 5, 2 )

Exercise 10.9. Find the equation of the circle that passes through
the two diametrically opposite points P1 and P1.
(a) Write out a strategy for solving this type of problem.
(b) P₁( 1, 3 ) and P₂( 3, 5 ) (c) P₁(−3, 1 ) and P₂( 4, 6 )

Normally, the circle is initially not in the center-radius form, but is
often in the general form. If you expand (multiply out) equation (12)
and write it in the form of a second degree equation, equation (2), you
get

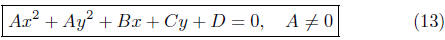
The equation is called the General Form for the equation of a circle.

Important Points. Notice the coefficients of the two squared terms are
equal (to A). This (almost) characterizes a second degree equation as
being a circle. It is also important to emphasize that the coefficients
of the squared terms have the same sign! For example, 2x² + 2y² +
x + y − 1 = 0 is a circle but 2x² − 2y² + x + y − 1 = 0 is not!

Here are a few quick visual manifestations of equation (13).

Illustration 3. Examples of Circles in General Form.

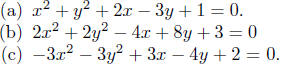
Here the common coefficient of
the squared terms is A = −3, that’s o.k. Needless to say, this
equation can be rewritten in a more esthetically pleasing form:
3x² + 3y² − 3x + 4y − 2 = 0.

Transforming to the Center-Radius Form. The center-radius
form is an “information yielding form” for a circle; therefore it is
beneficial to put an equation representing a circle into this form.

The Method of Transforming. Given an equation on the form of equation
(13), you can complete the square of the x-terms and complete
the square of the y-terms to obtain the center-radius form of the
equation of a circle.

Example 10.3. Put each of the following circles in the center-radius
form and find their center and radius.

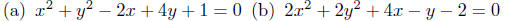
You see from the example the skills of needed to put an equation in
the center-radius form are skills you have been practicing in the past
several lessons. The other important skill is interpretation of results!
It doesn’t do you much good if you can’t extract the information
(center and radius).

I should mention, before we go to the exercises that not every equation
of the form (13) is a circle. Here are three very simple examples to

illustrate the possibilities:

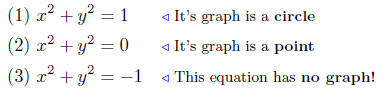
In (2), the only point (x, y) that satisfies the equation is (0, 0); hence,
its graph consists of a single point. (A degenerate circle?) In (3), there
is no point (x, y) that satisfies the equation, so there are no points on
the graph.

Exercise 10.10. Put each of the following into the center-radius
form. If an equation represents a circle, state its center and radius
and if it does not represent a circle characterize its graph.

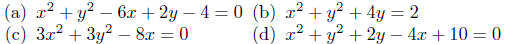
Exercise 10.11. Find the points of intersection between the two
given curves.

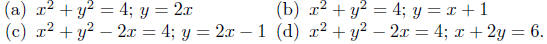
10.3. The Trig Functions

The trigonometric functions play an important role in many scientific
and technical fields as well as in many of the trades (carpentry comes
to mind). In this section we give a less than complete presentation of
some basic ideas.

• The Definitions and Consequences
The definitions of the trig functions are quite simple. For any number
t, we want to define cos(t) and sin(t). This is done using the unit
circle, x² + y² = 1.

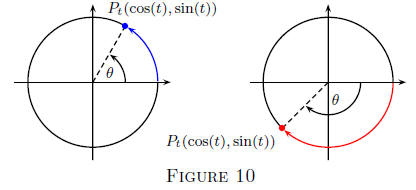
The Wrapping Definition of Sine and Cosine: Let t be any given real
number. Draw the unit circle x² + y² = 1. Beginning at the point
I( 1, 0 ), called the initial point, measure off a length of t units around
the unit circle; if t ≥ 0, mark off this length counter clockwise and
if t < 0, mark off |t| units in a clockwise direction. The point on the
circle at the end of your measurement process is called the terminal
point, (temporarily) denoted by Pt(x, y).

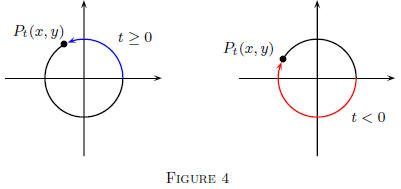
the terminal point is given by P_t(x, y), then define
 

cos(t) = x and sin(t) = y  (14)

 

That is, the cos(t) is defined to be the first coordinate of the terminal
point, and the sin(t) is defined as the second coordinate.

Let’s list off some simple consequences of this wrapping definition.

The Fundamental Identity for Sine and Cosine:
 

cos2(t) + sin2(t) = 1  (15)

 

This is because, by our definition, the cos(t) and sin(t) are the first
and second coordinates, respectively, of the terminal point Pt(x, y).
But Pt is a point on the unit circle and as such, its coordinates satisfy
the equation x² + y² = 1; therefore, cos²(t) + sin²(t) = 1 for any
number t.

Symmetry Properties of Sine and Cosine:
 

cos(−t) = cos(t) sin(−t) = −sin(t)  (16)

 

We say a function f(t) is an even function if it satisfies the equation
f(−t) = f(t) forall t in its domain; consequently, we may say that
cos(t) is an even function. A function f(t) is called an odd function if it
satisfies the equation f(−t) = −f(t) for all t in its domain; therefore,
we are entitled to say that sin(t) is an odd function.

The proof of equation (16) is given using the wrapping definition of
sine and cosine.

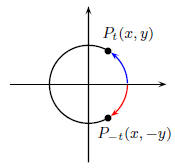
Think of t as positive. Measure t units counter
clockwise starting at I(0, 1) and terminating at
Pt(x, y). (This is shown in blue). By definition,
cos(t) = x and sin(t) = y. Now take the negative
number −t and measure off t units clockwise
around the circle, shown in red, to the terminal
point P_-t(x,−y). Because we are wrapping the
same length, but in opposite directions, the x-coordinate
of P_-t will be the same as the x-coordinate of P_t; the
y-coordinate of P_-t will be of negative the y-coordinate of P_t. Since
the terminal point of −t is P_-t(x,−y), by definition we have that
cos(−t) = x and sin(−t) = −y; but x = cos(t) and y = sin(t). Putting
these observations together we get

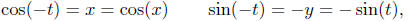
which are the symmetry properties.

Periodicity of Sine and Cosine:
 

cos(t + 2π) = cos(t) sin(t + 2π) = sin(t) (17)

 

In this case we say that cos(t) and sin(t) are periodic of period 2π. (In
general, a function f(t) is periodic of period p provided f(t+p) = f(t)
for all t in its domain. Not all functions are periodic.)

Again, this property is best seen through a picture.

For an y given number t, assumed to be positive
for the purposes of demonstration, wrap t
units around the unit circle, as shown in blue.
Denote the terminal point by P_t(cos(t), sin(t)).
Now compute the cosine and sine of the number
t + 2π. Begin by measuring off t + 2π units
around the circle; we do this by first measuring
off t units (shown in blue) followed by an additional
2π units (shown in red). Recalling that the circumference of the
unit circle is 2π, we see that when we wrap the additional 2π around,
we are just going in circles! :-) Therefore, P_t is the same as P_t+2π; in
words, the terminal point for the number t is the same as the terminal
point for the number t + 2π:

P_t(x, y) = P_t+2π(x, y).

It follows, from the wrapping definition, that

cos(t) = x = cos(t + 2π)  sin(t) = y = sin(t + 2π),

which are the periodic equations.

The Range of Cosine and Sine: We first observe that all coordinates
on the unit circle are between −1 and 1. Because the cos(t) and sin(t)
are coordinates on the unit circle, it follows
 

−1 ≤ cos(t) ≤ 1 − 1 ≤ sin(t) ≤ 1 (18)

• Some Common Values
In the age of the hand-held graphing calculator, why, you may ask,
should I know some of the common values of the sine and cosine? The
short answer is that some instructors, including yours truly, expect the
student to know these values. These values are among the “minimal
set of knowledge” anyone talking to you about the trig functions would
expect you to know. You want to be at least minimal, don’t you? :-)

The circumference of the unit circle is 2π. The numbers t = 0, t = π/2,
t = π, t = 3π/2, and t = 2π, when “wrapped” around the unit circle,
go zero of the way around, a quarter of the way around, a half of the
way around, three-quarters the way around, and all the way around,
respectively. The terminal points of these five values of t can be easily
observed:

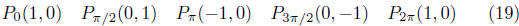
The coordinates of these “easy” points contain the cosines and sines
of the corresponding values of t. (Given in the subscript of the point,
I might add.)

• Quiz. As a test of your understanding of the wrapping definition,
and the meaning of the above notation, take the following quiz on
some of the common values of sine and cosine by clicking on the green
bullet.

Now let’s concentrate on three other values of t: t = π/6, t = π/4,
and t = π/3. These can be worked out rather easily, though it will
not be done in these lessons:

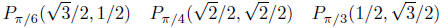
Look at the corresponding unit circle with these values wrapped.

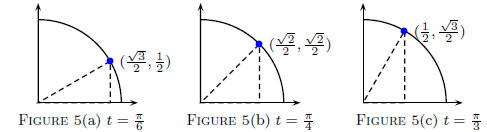
In Figure 5(a), we see that the cos(π/6) =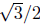 and sin(π/6) = 1/2.
These values correspond to the base and height of the right triangle.
(You can see that the height of the triangle is (about) 1/2 the radius
of the unit circle.) The companion values, shown in Figure 5(c), ar e
cos(π/3) = 1/2 and sin(π/3) =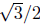. (Again notice the base is of the
triangle is about 1/2 the radius.) Finally, Figure 5(c) tells us that
cos(π/4) =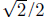 and sin(π/4) =.

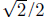Here is a table and figure summarizing the values of sine and cosine.

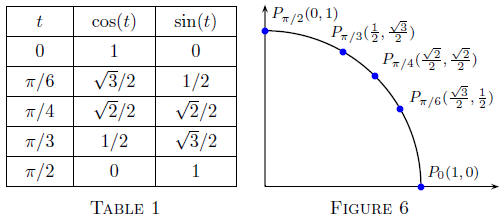
By utilizing the symmetry property, the periodic property, and the
wrapping definition of sines and cosines you can easily calculate any
integer multiple of π/n, where n = 1, 2, 3, 4, 6. In particular, it is important
to keep a visualization of the wrapping pictures of Figure 4.

In the example that follows, I exhibit the simple reasoning necessary
to calculate any value integer multiple of π/n, for n =1, 2, 3, 4, 6.

Example 10.4. Calculate the exact value of each of the following:
(a) sin(−π/3) (b) cos(2π/3) (c) cos(5π/4) (d) sin(−π/2)

Tip. How to Determine Values of Sine and Cosine: To calculate the
sine or cosine of multiples of π/n (n = 1, 2, 3, 4, 6) (1) draw a unit
circle; (2) plot the terminal point (this may require division, e.g.,

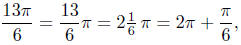
thus, 13π/6 is π/6 “beyond” 2π); (3) observe the relation between this
point and one of the terminal points given in Table 1; (4) calculate
value with the proper sign affixed.

Note. It is actually only necessary to wrap clockwise; i.e., you need
only deal with positive values of t. This is because of the symmetry

properties; thus,

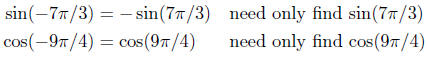
Exercise 10.12. Find the values of each of the following without the
aid of a calculator.

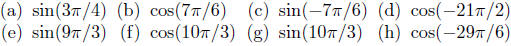
• Graphs of the Trig Functions
Having defined, for an y number t, the cos(t) and sin(t), we now want
to study them as functions. Usually, the independent variable of a
function is x, not t. Replace the letter t by the letter x to obtain two
trigonometric functions:
y = cos(x) y = sin(x)
In this brief section, we remind the reader of the graphs of these two
functions.

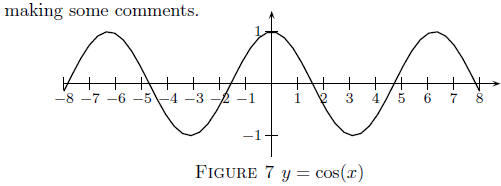
The Graph of y = cos(x). Let us begin graphing the cosine and

The fact that the graph is symmetric with respect to the y-axis is a
manifestation of the even function property of the cosine. The regular,
repeated behavior of the graph is the periodicity of the cosine. The
cosine function repeats its pattern of values over consecutive intervals
of length 2π, the period.

The x-intercepts of the cosine are all values of x for which cos(x) = 0.
Based on the wrapping definition of the cosine, it is easy to see that
the x-intercepts are

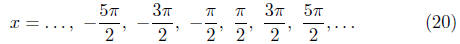
Or, in other words, the graph of y = cos(x) crosses the x-axis at all
odd multiples of π/2. This is an important point.

The cos(x) attains its maximum value of y = 1 at

x = . . . ,−4π,−2π, 0, 2π, 4π, . . . (21)

In other words, cos(x) takes on its maximum value at all even multiples
of π.

Exercise 10.13. List, in a style similar to equation (21), the values
of x at which the cos(x) takes on its minimum value of y = −1.
Having done that, write a good English sentence that describes these
numbers. (See the sentence that follows equation (21) above.)

The Graph of y = sin(x). Let us begin graphing the sine and making

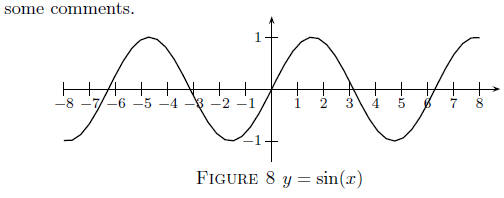
The sine function is an odd function; the graph of an odd function is
symmetrical with respect to the origin. The regular repeated behavior
is the periodicity of the sine function. The sine function repeats its
pattern of values over consecutive intervals of length 2π, the period.

Exercise 10.14. The x-intercepts. List out the x-intercepts of y =
sin(x) using the style of equation (21), then describe this set of points
using a good English sentence. (References: Table 1 and Figure 8.)

Exercise 10.15. Maximum Values of sin(x). List the values of x
at which the function y = sin(x) attains its maximum value of y = 1.
Then describe these numbers in a good English sentence.

Exercise 10.16. Minimum Values of sin(x). List the values of x
at which the function y = sin(x) attains its minimum value of y = −1.
Then describe these numbers in a good English sentence.

The Two Graphed Together: It may be useful to view the graphs of
the sine and cosine on one sheet of electronic paper in order to make

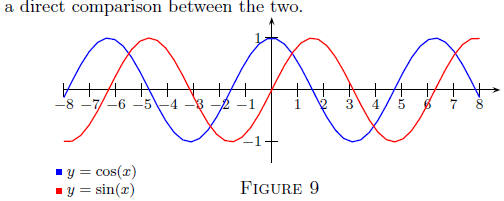
Notice that the graphs of y = cos(x) and y = sin(x) appear to be
identical; identical in the sense that one graph, say y = cos(x), can
be obtained by shifting the graph of y = sin(x) to the left. This
observation is in fact correct; more precisely. The cosine graph can be
obtained from the sine graph by shifting the sine graph over π/2 units
to the left.

• The Other Trig Functions
There are four other trig functions that hitherto I have failed to mention.
Their definitions are in terms of cos(x) and sin(x). These four
are the tangent, cotangent, secant, and cosecant functions:

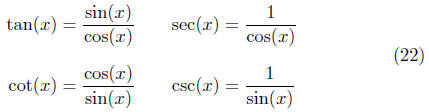
Of course, we make these definitions for all values of x for which the
denominators are nonzero .

The trigonometric functions play diverse roles in mathematics.
• They are quite commonly used to develop relationships between
the sides of right triangles. These relationships are important in
applications in such different fields as carpentry, architecture,
surveying, navigation, and computer graphics . . . to name just
a few.
• In Calculus, these functions are studied like any other function.
The trigonometric functions enable us to solve a greater variety
of problems that require the special techniques of calculus.
Having trigonometric functions enables scientist and engineers
to properly formulate and solve complex problems, often with
the aid of calculus and geometry.

The interesting and very useful applications must be reserved for a
proper course in algebra, trigonometry, calculus, and/or courses in
specialized fields. These lessons are meant as a minimal review of
bygone memories.

Example 10.5. Identify the domain of definition of the function y =
tan(x).

Quick Quiz. Is the domain of sec(x) the same as that of tan(x)?
(a) Yes (b) No

Exercise 10.17. Identify the domain of definition of the function
y = cot(x). (Hint: The domain would be all values of x for which the
denominatoris nonzero.)

• Radian Measure versus Degree Measure
The wrapping definition of sine and cosine tells us how to compute
the sine and cosine of a number t. The number t is not interpreted as
an angle, but was simply any real number . Within the context of the
wrapping definition, the number t is said to be measured in radians.

What is angle measurement? As you wrap the number t around the
unit circle, you are revolving around the center of the circle The distance
around the circle is its circumference 2π; one complete revolution
around the circle is referred to as a 360◦ revolution.

In this case we say 2π radians is the same as 360◦ (degrees). The
degree measurement of an arbitrary number t is calculated by direct
proportions; let the symbol θ denote the degree measurement of t,
then using direct proportions:

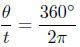
or

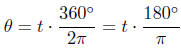
The number180 /π is referred to as the scaling factor for converting
radians to degrees.

Converting Radians to Degrees: Let t be a number (measured in radians). The degree measurement of t is given by

Illustration 4. Calculate the degree measurement of each of the following.
by applying the conversion formula, equation (23).

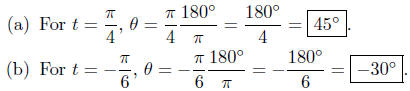
This is not hard so I’ll just ask you to make a few calculations yourself.

Exercise 10.18. Calculate the degree measurement of each of the
following. by applying the conversion formula, equation (23).

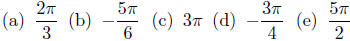
In the same way we can convert degrees to radians by simply solving
the equation (23) for t:

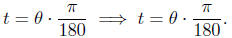
Elevating this to the status of shadow box we obtain the following.

Converting Radians to Degrees: Let θ be a number measured in degrees. The radian measurement of θ is given by

Applying this formula is the same as applying the conversion formula
(23) so no examples will be presented.

Exercise 10.19. Convert degrees to radians in each of the following.

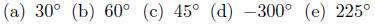
Naturally, if θ is a number measured in degree, we naturally define
cos(θ) = cos(t) and sin(θ) = sin(t), where t is the radian measurement
of θ, as computed by equation (24). For example,

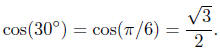
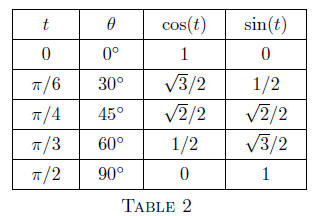
Let’s revisit Table 1 and include degree measurement. Below is a
table of common values of sine and cosine that you should and must
know.

The angle measurement is usually seen in the context of problems
involving triangles. These problem types will not be covered in these
lessons—sorry.

As a final set of thoughts, let’s connect up the geometric relationship
between radian measure and degree measure.

The degree measure is a measure of how many times we wrap around
the unit circle based on 360◦ rather than 2π, as is the case of radian
measure. The student needs to be able to move quickly and quietly
between these two systems of measurement.

This point represents the end of our Algebra Review in Ten
Lessons. It ended not with a bang but a measure!

If you have waded through all ten lessons, my hearty congratulations
to you. There was much of algebra and trigonometry not covered in
course, but a review of basic concepts and techniques.

In additional to the basic techniques and ideas presented, I hope you
come away from these lessons with the ability to use good and standard
notation and to present your thoughts in a clear and concise manner.
This would be most appreciated by your professors, and is a sign of
your mathematical maturity.

I hope these imperfect lessons have helped you review some of the
basics concepts your professors will assume you know. Now, on to


To exit, either go to the top of this file and follow the arrows, or simply
click here.

Solutions to Exercises

10.1. Solution: We simple complete the square!
Solution to (a). Analyze: y = x² − 6x.

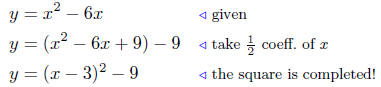
Now we put this last equation in standard form:
 

y+9 = (x − 3)2

 

We see this is a parabola that opens down and has its vertex at
V ( 3,−9 ).

Solution to (b) Analyze: y = 1− 4x − x².



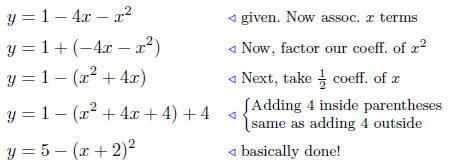
Now write the last equation in standard form:
 

y −5 = −(x + 2)2

This is a parabola that opens down and has its vertex at V (−2, 5 ).

Solution to (c) Analyze: x² + 2x + y+1 = 0.

Begin by writing the equation as a function of x;

y = −1 − x² − 2x

and not continue as before:

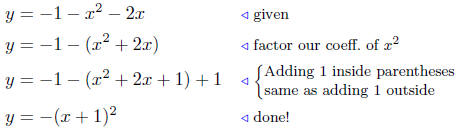
Summary: This is a parabola that opens down having vertex located
at V (−1, 0 ). (Here, relative to the notation of the standard form,
k = 0.)

10.2. Solution to (a) Analyze: y = 4x² + 2x + 1.

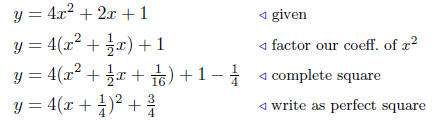
Summary: The equation in standard form is



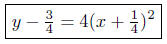
This is a parabola that opens up and has vertex at V (−1/4, 3/4).

Solution to (b) Analyze: 2x² − 3x − 2y + 1 = 0. Begin by solving for
y as a function of x:



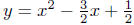
and proceed using standard techniques.

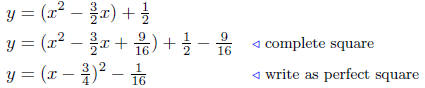
Summary: The equation written standard form is



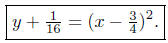
This equation describes a parabola that opens up and has its vertex
at V ( 3/4,− 1/16 ).

Solution to (c) Analyze: x − y = 4x². Begin by solving for y as a
function of x:
 

y = −4x2 + x

and complete the square.

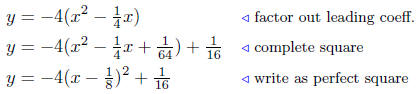
This last equation written is standard form is

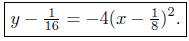
This is a parabola that opens down with vertex as V ( 1/8, 1/16 ).

Solution to (d) Analyze: 3x² + 2x + 4y − 2 = 0. Write as a function
of x:


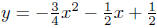
and complete the square.

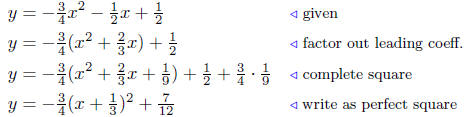
Summary: Write in standard form:



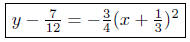
This equation represents a parabola that opens down and has vertex
at V (−1/3, 7/12 ).

Remarks: As you can see, these are all solved exactly the same way.
The only difference is the level of difficulty in completing the square.

This is why fundamental algebra is so important: It is used to extract
information. Unless you can perform the algebra, you cannot extract
the information—not good in the information age!

10.3. Solutions
(a) Find the x-intercepts of y +1 = (x − 1)². We use standard
methods. To find the x-intercept, we put y = 0 and solve for x.

1 = (x − 1)² or( x − 1)² = 1

We now solve for x:

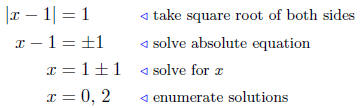
Presentation of Answer: The x-intercepts are x = 0, 2.

(b) Find the x-intercepts of y+1 = 2(x − 1)². Put y = 0 and solve
for x.

1 = 2(x − 1)² or( x − 1)² = 1/2

Now solve for x:

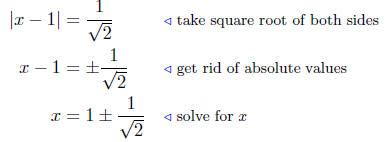
Presentation of Answer: The x-intercepts are at



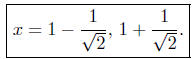
Notice they are symmetrically placed on either side of the vertex.

10.4. Solution: Your rough graphs should roughly look like the following:

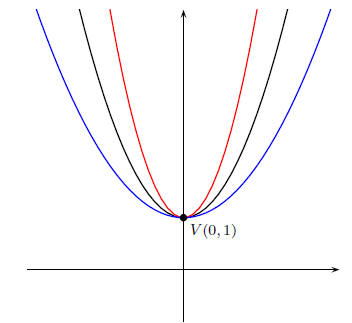
Legend:
y = x² + 1;
 y = 2x² + 1;

10.5. Solutions: Here are outlines of the solutions.

(a) Analyze: 4x + y − x² = 1.

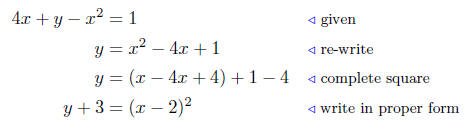
Summary: This is a parabola that opens up with vertex at V ( 2,−3 ),
the sketch is left to the reader.

(b) Analyze: y = −x² − 6x + 1.

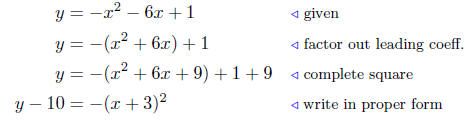
Summary: This is a parabola that opens down and having vertex at
V (−3, 10 ).

(c) Analyze: 2x − 3y = x².

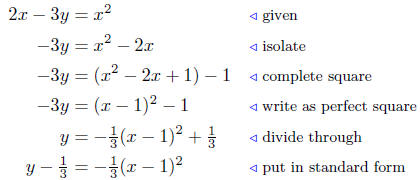
Summary: This is the equation of a parabola that opens down with
vertex at V (1, 1/3).

Exercise Notes: In this last part, I did something a little different.
I completed the square of the l.h.s. before dividing through by the
coefficient of y; this was to avoid working with fractional expressions
unnecessarily. Many of the previous examples and exercises could have
been handled the same way.

10.6. Solution to (a) Analyze: x + 2y = y².

First write the equation as a function of y:

x = y² − 2y.

Now, complete the square

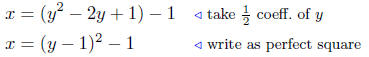
Summary: The equation written in standard form is
 

x+1 = (y − 1)2

This is a horizontally oriented parabola (since y has degree 2 and x
has degree 1), it opens to the right (since the coefficient of the y² term
is positive), and its vertex is located at V ( ,−1, 1 ).

The sketch of the graph is left to the student—that’s you.

Solution to (b) Analyze: 2x − 4y + y² = 3.

Begin by solving for x; writing x as a function of y:



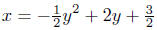
Now, complete the square!

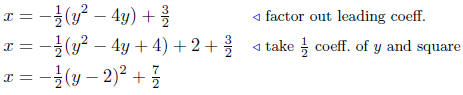
Summary: The equation written in standard form is



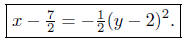
This describes a horizontally oriented parabola that opens left with
vertex at V ( 7/2, 2 ).

The graph is left to the student, but don’t plot too many points. Three
are enough!

Solution to (c) Analyze: 2y² − 4y + x = 0.

Write x as a function of y:

x = −2y² + 4y

and complete the square

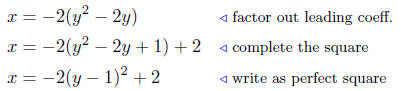
Summary: The parabola written in standard form is
 

x −2 = −2(y − 1)2.

It opens left with vertex at V ( 2, 1 ).

The graph is left to the student.

Ever get the feeling you have done this before?

Solution to (d) Analyze: 2x + 3y + 4y² = 1.

First write the equation as a function:



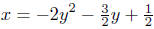
and now, complete the square,

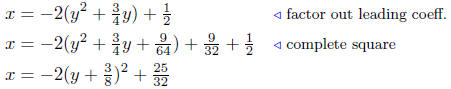
Summary: The equation written in standard form is



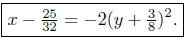
It opens to the left and has vertex at V ( 25/32 ,−3/8).

The graph is left to the student.

10.7. Solution to (a) To find where two curves intersect we set the y-coordinates
equal and solve for x. In this case, the resulting equation
has the second degree, so we can anticipate solving either using the
method of factoring, or, most likely, using the Quadratic Formula.

Solution to (a) Find where y = 2x + 1 and y = x² + 2x − 1 intersect.
First not that this is the intersection of a line and a parabola. They
will either not intersect, intersect at one point, or intersect at two
points. (Can you visualize each situation?) Let’s see which one it is in
this case.

Begin by setting the ordinates equal.

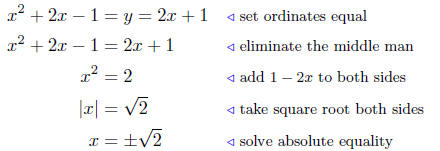
Summary: The two curves intersect at two points: When the abscissas
are x = −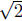 and x =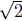. “Plugging” these values of x back into the
straight line, we can calculate the coordinates of intersections:

Points of Intersection: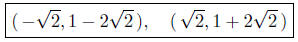

Solution to (b) y = 2x + 1; y = x² + 4x − 1

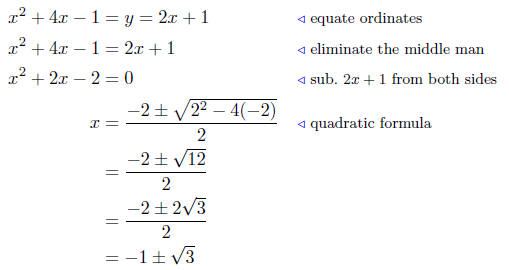
Summary: The abscissas of intersection are

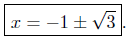
The interested reader can go on to calculate the coordinates of intersection
just as I did in part (b).

Solution to (c) y = x² + 2; y = 2x² − 3x + 3. This is the intersection
of two parabolas that open up.

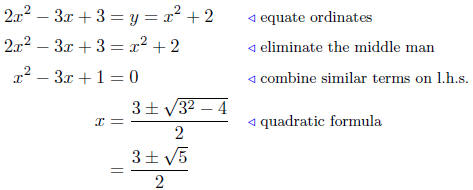
Summary: The abscissas of intersection are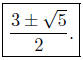

Solution to (d) y = x² + 2; y = 4 − (x − 1)². These again are two
parabolas, one opening up, the other down.

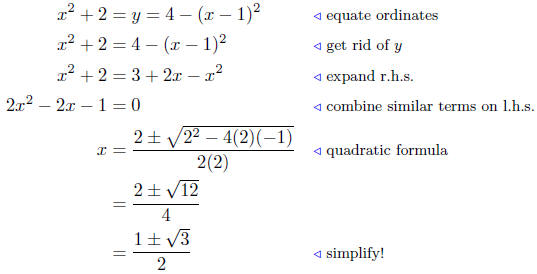
Summary: The abscissas of intersection are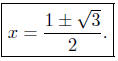

10.8. Solution to (a) We are given the center C of the circle and one
point, P, on the circle. All we need is the radius of the circle. From
equation (10) we have

d( P,C ) = r

or

r = d( P,C ).

 

This boxed formula represents the method of solving these problems

Solution to (b) We already have the center of the circle, we need the
radius.

We follow the plan of attack developed in (a):

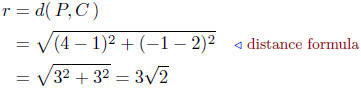
Thus, r = 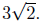The equation of the circle is

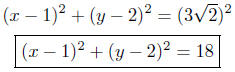
Solution to (c) As in the part (a), r = d(P,C), where C(−2, 3 ) and
P( 5, 2 ).

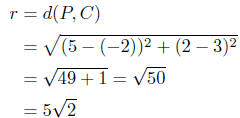
The equation is for the desired circle is

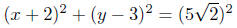
or

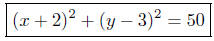
10.9. Solution: Since the two points P₁ and P₂ are diametrically
opposite, the radius is given by



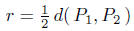
The center of the circle is the midpoint of the line segment P₁P₂;
simple use the midpoint formula.

Solution to (b) P₁( 1, 3 ) and P₂( 3, 5 ).

I follow my own game plan:

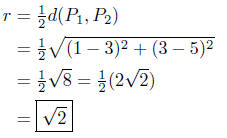
The center is the midpoint between P₁( 1, 3 ) and P₂( 3, 5 )

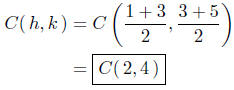
The equation of the circle is

(x − 2)2 + (y − 4)2 = 2

Solution to (c) P₁(−3, 1 ) and P₂( 4, 6 )

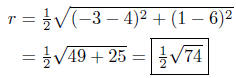
The center is the midpoint between P₁(−3, 1 ) and P₂( 4, 6 ):

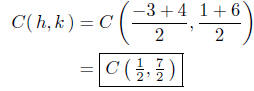
The equation of the circle is

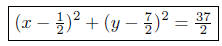
where we have calculated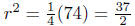

10.10. Solution to (a) x² + y² − 6x + 2y − 4 = 0

We complete the square and interpret the result.

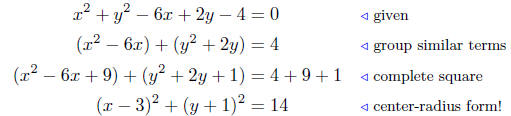
last equation is in the center-radius form. It represents a circle
with center at C(3,−1) and radius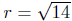

Solution to

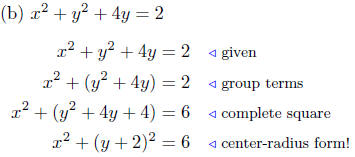
This is the equation of a circle with center at C(0,−2) and having
radius of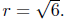

Solution to (c) 3x² + 3y² − 8x = 0

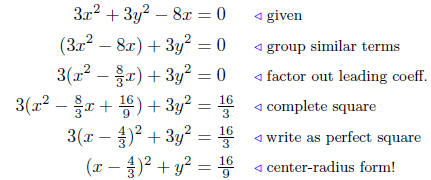
This is the equation of a circle with center at C(4/3, 0) and radius r = 4/3

Solution to (d) x² + y² + 2y − 4x+10 = 0

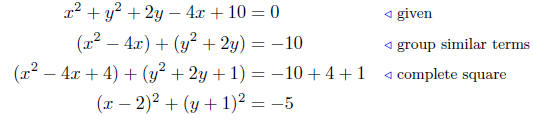
The equation (x − 2)² + (y + 1)² = −5 does not describe a circle
since the number on the right-hand side is negative. There is no point
(x, y) that satisfies this equation since the left-hand side is always
nonnegative and the right-hand side is negative. This equation has no
graph.

10.11. Solution to (a) Find the points of intersection between x² +
y² = 4 and y = 2x. We equate the ordinates and solve for x. The
easiest way of doing this is to substitute the value of y into the other
equation:

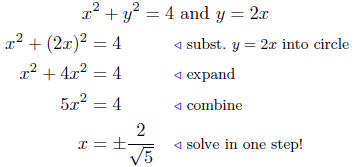
These are the abscissas of intersection. To obtain the corresponding
ordinates, simple substitute these values into y = 2x to obtain the
coordinates of intersection:

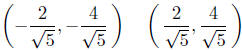
Solution to (b) Find the points of intersection between x²+ y² = 4
and y = x + 1.

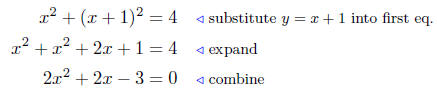
Now apply the Quadratic formula:

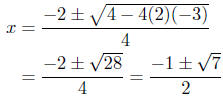
Summary: The abscissas of intersection are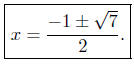

The corresponding y-coordinates (the ordinates) can be obtained by
substituting these abscissas into the straight line equation: y = x+1.
I leave this to you.

Solution to (c) Find the points of intersection between x²+y²−2x = 4
and y = 2x − 1.

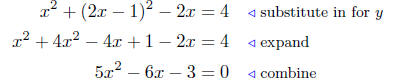
Now apply the Quadratic Formula:

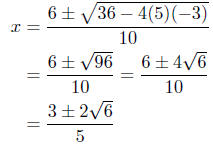
Summary: The abscissas of intersection are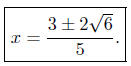

Solution to (d) Find the points of intersection between x²+y²−2x = 4
and x + 2y = 6.

In this case, I think I’ll do something a little different. I’ll solve for x
in the second equation, x = 6 − 2y and substitute this into the first
equation. This is to avoid working with fractions when it is really not
necessary to do so!

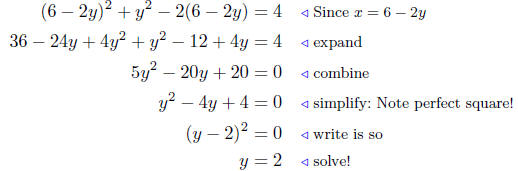
In this case, there is only one point of intersection:

y = 2 and x = 6− 2y => x = 2

Thus,

Point of Intersection: (2, 2)

If you draw the graphs of these two, the circle and the line, you will
see that the line is tangent to the circle at the point (2, 2).

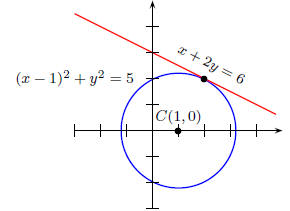
Never mind, I did it myself!

10.12. Solutions: The following answers are given without extensive
discussion. If you don’t see how I got the number, follow the tip given
above.

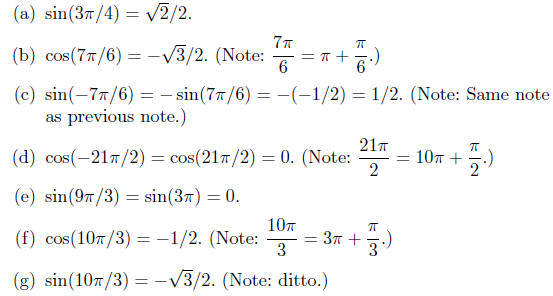
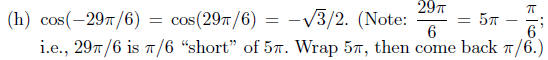
Exercise Notes: I could have done part (h) in a way that is consistent
with how I did the others:

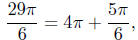
Therefore,

cos(29π/6) = cos(5π/6)

Now I would need to compute cos(5π/6). I found it much easier to
realize that 29π/6 was π/6 “short” of 5π.

Though I didn’t refer to the property explicitly, what we are in
fact doing is using the periodic properties. In the previous remark,
when I write

cos(29π/6) = cos(5π/6)

That is the periodic property of the cosine. To wrap around an amount
of 29π/6 you first wrap 4π which is twice around the unit circle, then
you go another5 π/6.

10.13. The values of x at which cos(x) takes on its minimum value
of y = −1 is

Prev

Next