Math Study Sheet for Test 2
For all the GCF/ LCM problems , you are expected to use (and to show) the
methods we learned in class.
Assume all letters represent counting numbers.
1. Indicate whether each statement is true or false:
a) 6 is a multiple of 12.
b) Any multiple of 9 will also be a multiple of 12.
c) If a number is made up of 18’s, it is also made up of 4’s.
d) Any counting number that is not prime is composite.
e) 1 and m are relatively prime.
f) If two different numbers are prime, then they must be relatively prime.
g) Any counting number which is not prime must be composite.
h) The GCF of 6x and 7x is x.
i) The LCM of two different prime numbers is their product .
j) The LCM of n and 1 is 1.
k) If the numerator of a fraction is less than a third of the denominator, then
the fraction is less than 1/3.
l) If the numerator of a fraction is exactly 4/5 ths of the denominator , then
the fraction is less than 4/5.
a) If LCM(x, y) = 16, then x is a multiple of 16.
b) If a and b are relatively prime, then GCF(a, b) = b.
c) If GCF(m, n) = 6, then n is a factor of 6.
d) If a is a factor of b and a ≠ b, LCM(a, b) = b.
e) GCF(a, 1) = a.
f) If a and b are both multiples of 3, they are relatively prime.
g) Two consecutive odd numbers are always relatively prime.
1. List all the factors of 48.
2. Systematically list all the factors of
.
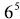Write them in their prime factorizations.
3. Systematically list all the factors of
.
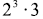Write them in their prime factorizations.
4. Name two numbers, both above 20, that are relatively prime.
5. Explain: any multiple of 5 that is greater than 5 must be composite.
6. What is the definition of composite?
7. Find the smallest composite number which is not divisible by any counting
number between 1 and 50.
8. Name two different numbers , both between 20 and 300, that have a GCF of 15.
9. Name two different numbers that have an LCM of 30.
10. Suppose Chris and Jean have different work schedules. Chris has every 4th
day off, and Jean has 3rd day
off. (If they both worked April 30th, Chris will be off on May 4th and May 8th
and Jean will be off May 3rd
and May 6th) Which of them will be off on May 30th? What is the first day in May
they will both have
off?
11. Find, using the technique we used in class, LCM(24,
45).
12. Find, using the technique we used in class, GCF(350, 630).
13. Name three pairs of numbers that have an LCM of 100.
14. What is the name of the “filter” which can be used to find prime numbers in
the first n counting numbers?
Briefly explain how one uses this “filter.”
15. When using the “filter” described in problem 14, what would be the first
number one would cross out after
circling 73? Write the answer in its prime factorization.
16. What pairs of numbers have a GCF of 3 and an LCM of 42? (List all of the
possibilities.)
17. What pairs of numbers have a GCF of 6 and an LCM of 42? (List all of the
possibilities.)
18. If GCF (x, 42) = 6 and LCM (x, 42) = 252, find x.
19. If GCF (x, 85) = 5 and LCM (x, 85) = 850, find x.
20. If GCF (x, 18) = 2 and LCM (x, 18) = 504, find x.
21. Name two numbers between 200 and 1000 that have a GCF of 9.
22. Evaluate:
a) GCF (x, 3x) =
b) LCM (4b, b) =
c) GCF (a, 4 ) =
d) LCM (n, 1) =
e) LCM (p, q) if p and q are different prime numbers
f) LCM (2p, 3q) if p and q are different prime numbers
g) LCM(6p, 10q) if p and q are different prime numbers
h) GCF(1, a, 3a)
i) LCM(1, a, 3a)
23. If the GCF(x, 32) = 16 and the LCM(x, 32) = 96, find
x.
24. If the GCF(m, 48)= 3 and LCM(m, 48)= 432, find m.
25. If the GCF of two numbers is 8 and their LCM is 320, what could the numbers
be? (List all the
possibilities.)
26. Name three pairs of numbers x and y, so that
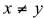, neither x nor y is a multiple of 7, and
GCF(x, y) = 4.
27. Name three pairs of different odd numbers that have a GCF of 15.
28. A student claims that all multiples of 3 are composite. Is he correct? Why
or why not?
29. Find two numbers that have a GCF of 20 and an LCM of
280. Find three pairs (6 different numbers, if
possible).
30. Find two numbers m and n so that m and n are both greater than 100,
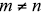, and GCF(m, n) = 21.
31. Find 3 different pairs of numbers x and y, so that
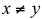and LCM(x, y) = 300.
32. Find all possible pairs of numbers that have an LCM of 121.
33. Find a pair of numbers that has a GCF of 12 and an LCM of 420.
34. Suppose that Terry has 3/11 of a pizza and Todd has 5/8 of an identical
pizza. Circle all statements that are
clear, complete, and correct:
a) Terry has more pizza because 11 is larger than 8.
b) Todd has more pizza because 5 is larger than 3.
c) Todd has more pizza because he has more pieces and his pieces are larger than
Terry’s.
d) Todd has more pizza because 8ths and larger than 11ths.
e) Terry has less pizza because 11ths are smaller than 8ths.
f) Terry has less pizza because he has less than 1/2 and Todd has more than 1/2.
g) Todd has more pizza because Terry has about 1/4 of a pizza and Todd has about
1/2.
35. Decide which fraction is larger by comparing each
fraction to 1/2. Clearly write your reasoning and your
conclusion.
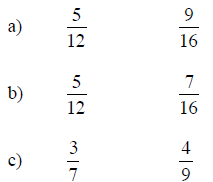
36. Decide which fraction is larger by comparing each fraction to 1.
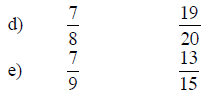
36. Suppose Terry decides to give his son Paul 3 times as
many brownies as he gives his son Will. Could this
possible be fair? If so, how?
37. Suppose Andy has 2/5 of a pizza and Abby has 6/13 of an identical pizza. Fill in the blanks:
Andy complains that he has _________ pieces of pizza than
Abby does. In fact, he notices that Abby has
___________ _____________ as many pieces as he does. Abby says that this could
be fair—that they
have to look at the ___________ of their slices. Andy says that the only way
this can be fair is if Abby’s
pieces are __________ ___________ smaller than his. Abby says that means her
pieces should be 15ths.
Since her pieces are _________________ than 15ths, _______________ has more
pizza.
38. Suppose Franklin states that 3/4 is equal to 7/8
because both fractions are missing 1. Is his reasoning
correct? Why or why not?
| Prev | Next |