Statistics for Sociologists

Goals of This Module

• Start with a discussion of looking at simple relationships
between categorical dependent and independent variables
 • Converting to proportions , percentages and ratios
 • Contingency tables (cross-tabulation)
 • Partial tables for multivariate relationships
  • Problem of Simpson’s Paradox
• Revisit multiple regression , considering categorical
explanatory variables (dummy variables)
 • Look at both main effects ( difference in intercepts ) and
interaction effects ( difference in slopes )
• Question of causation
 • Establishing causation

Converting Raw Numbers to Proportions , Percentages or
Ratios

• Raw numbers (i.e, simply the number of cases in a particular
category) can often be difficult to interpret, especially if there
are several categories and an awkward number of total cases
• Percentages and proportions (and ratios) are also much easier
to compare both with variables and across variables
• Cautions:
 • We must be careful not to over-interpret percentages (or
proportions) based on small total sample sizes
 • Tables containing proportions or percentages should always
contain the sample size (n)

Proportions

• It is often useful to convert raw numbers to proportions,
especially when comparing categories
• The formula to find a proportion is simply:

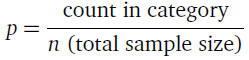
• If there are 60 students in the class, 46 of whom are women,
what is the proportion of women? Here count = 46 and
n = 60, therefore
p = 46/60 = .77

• In other words, the proportion of women in the class is .77.
• Since the total equals 1, the proportion of men is 1-.77 = .23

Percentages

• A percentage gives us the same information as a proportion
except we now multiply the proportion by 100:

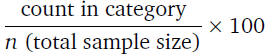
• Continuing from the proportions example, if there are 60
students in the class, 46 of whom are women, what is the
percentage of women? Here count = 46 and n = 60,
therefore

p = (46/60)*100 = 77%

• In other words, 77% of the class are women
• Since the total for percentages equals 100, the percentage of
men is 100-77 = 23%

Ratios

• Ratios allow us to directly compare the relative number of
cases in one category compared to another:

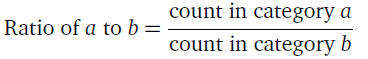
• If there are 46 women and 14 men, the ratio of women to
men is:

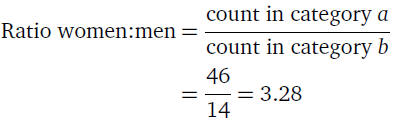
• In other words, there are more than 3 times as many women
as men in the class

Bar Graphs and Pie Charts revisited (1)

Bar charts should be used over pie charts – research indicates
that people are better able to judge the relative difference in
size of straight lines than pie shapes

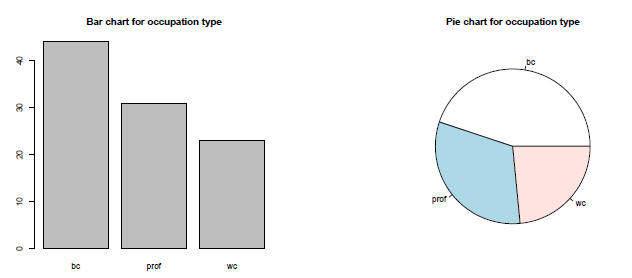
> plot (type, main="Bar chart for occupation type")
> pie(table(type), main="Pie chart for occupation type")

Bar Graphs and Pie Charts revisited (2)
An Alternative to the Bar graph & Pie Chart: the Dot Chart

• The dot chart is an
alternative to the bar graph
or pie chart. It is especially
useful for displying
multivariate tables (see
later)

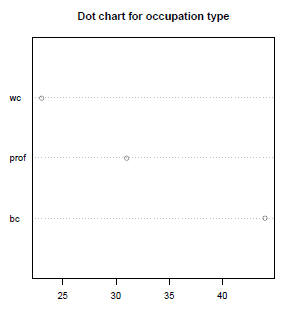
> par(pty="s")
> dotchart(table(type), main="Dot chart for occupation type")

Bar Graphs and Pie Charts revisited (3)
Critique of pie chart by Cleveland (1994, Figures 4.19 p. 262 and 4.20 p. 263)

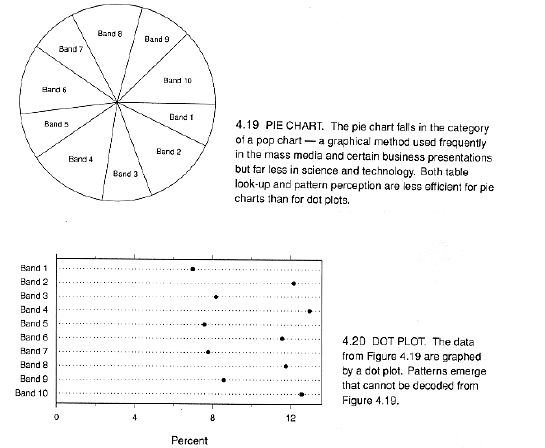
Contingency Tables

• Also called Cross-Tabulations
• Display relationships between categorical variables
 • Remember: With qualitative variables we talk of relationships
or associations, but NOT correlations.
• Cells of the table represent the number of observations that
fall simultaneously into a particular combination of two
categories of the two variables .
• Tables can be presented in several ways:
 1. Raw counts or frequencies
 2. Percentages (or proportions) of total N
 3. Percentages (or proportions) of column Ns
 4. Percentages (or proportions) of row Ns