Technology Tools used

Technology Tools used: Computer, Internet, and Graphing Calculator

OVERALL OBJECTIVES:

A.N.6
Evaluating expressions involving factorial(s), absolute value(s), and exponential
expression(s)

A.A.13
Add, subtract, and multiply monomials and polynomials

A.A.12
Multiplication/Division of monomials expressions with a common base using the
properties of exponents (integral exponents only)

A.A..14
Divide a polynomial by a monomial or binomial (quotient has no remainder)

MATERIALS USED:

Overhead projector
Computer
Transparencies
Student worksheets
Student notes
Student homework
Algebra tiles
Cardboard algebra tiles for students

OUTLINE

POLYNOMIALS
Day 1	Adding and Subtraction: After filling in note sheets students will engage in a hands on activity using card board algebra tiles.
Day 2	Exponents: After filling in note sheets students will engage in an interactive computer activity that allows them to do many different examples of exponents.
Day 3	Multiplying: After filling in note sheets students will use NVLM to assist them in solving polynomial problems.
Day 4	Dividing: After filling in note sheets students will engage in an interactive computer game that quizzes them on their skill of dividing polynomials
Day 5	Factoring: After filling in note sheets students will work in groups to complete a worksheet with many examples on it.

DAY 1: Adding and Subtracting Polynomials

Lesson Summary

Students will be able to identify and differentiate between monomials, binomial, and
trinomials, and other polynomials

Students will be able to define monomials, binomials, trinomials, and polynomials in
their own word.

Students will be able to effectively add and subtract polynomials and be able to explain
the correlation between the two.

Students will be able to identify coefficients of a polynomial

Students will be able to use algebra tiles to add and subtract polynomials

Materials:

Teacher:

Describe what materials the teacher will need.

• Overheard projector
• Note Sheet Transparency
• Algebra Tiles

Student

• Student note sheet
• Pencil
• Algebra tiles (made of card board )
• worksheet

NYSED Standards addressed in this lesson:

A.N.6
Evaluating expressions involving factorial(s), absolute value(s), and exponential
expression(s)

A.A.13
Add, subtract, and multiply monomials and polynomials

Description of the Lesson

Exercise 1
During the lesson I will have an overhead transparency with the notes while the students
will have a copy of the notes. Students will fill in the areas of the notes as we go through
the lesson.

• I will write on the overhead 2³ . I will tell the students to think about what I wrote on
the board and recall how we would solve the problem. I will take a few student
responses. We will then review that you solve the problem as follows: 2 x 2 x 2
2³ = 2 x 2 x 2.

• I will then pose the question: What if we change the 2’s into x’s. How would we
solve the problem? The same way? x³ = ? I will take a few student responses and
then go over that x³ = (x) (x) (x)

• I will then ask the students, what if we put a number in front of the x.
Example: 4x³
I will tell the students that the 4 in the equation is called a coefficient. I will review
the definition of a coefficient.
Coefficient: a number in front of the x that is multiplied in with the x’s.
4x³ = (4) (x) (x) (x)

• On the board we will do another example. I will write 5x⁴ . I will ask students, what is
the coefficient? After taking a few student responses, I will make sure students
understand the concept of coefficients.

• I will write on the overheard the word polynomial. I will ask the student what they
think a polynomial is. After taking a few responses, I will give the students the formal
definition.

Polynomial: products of numbers and letters where the exponents on the variables are
non-negative integers.

I will ask the students what they think the word “poly” means. I will review with the
students that the term “poly” means many. Therefore, polynomials are an equation
that contains many terms. I will write the on the board the example x² - 4x + 1
I will tell the students that this is an example of a polynomial. I will ask a student to
give me another example of a polynomial.

• On the overhead, I will have the three following terms: Monomial, Binomial, and
Trinomial. I will tell the students to underline the beginning of each word
(monomial, binomial, trinomial). I will give the students a minute to think about what
each word means. As a class we will go over them.
Monomial: A polynomial with one term. Ex: 5x
Binomial: A polynomial with two terms. Ex: 3x + 5
Trinomial: A polynomial with three terms. Ex: x² + 3x + 5

I will tell the students that if we have more than 3 terms we do not have any fancy
names for the equation but we strictly just call is a polynomial.

• I will tell the students to look at the following problem: 2x³ + 1. I will tell the
students that we are going to learn how to find the degree of the polynomial. I will tell
the students that to find the degree of a polynomial we have to look for the leading
coefficient. I will tell the students that the degree of a polynomial is the largest
degree of all its terms. I will ask the class what they think the degree of 2x³ + 1 is? As
a class we will conclude that the degree of the problem is 3. I will as the class what if
we the following: 8. What is the degree of 8? After taking a few student responses, I
will explain to the class that is a zero degree polynomial because coefficients have
nothing to do with the degree. I will practice the concept of finding the degree of a
polynomial with the students by doing the following examples:3x - x² and a⁴ b - 5a² b

• I will tell the students that we are now going to learn to add and subtract polynomials.
I will introduce to the students algebra tiles. I will show which each one represents
and I will demonstrate with an example. I will make sure students understand that the
yellow algebra tiles represent positive numbers and the red algebra tiles represent
negative algebra tiles.

Represents x²

Represents x

Represents 1

• I will ask the students how do you think we would represent x² + 5x + 6? I will
show the students using the algebra tiles that we would use one x² , five x’s , and
six ones. As a class we will do another example: 2 x² 3x + 5. I will tell the
students that using algebra tiles we can not only represent an equation but we cal
also ass and subtract polynomials. I will tell the students that before we use the
algebra tiles to add and subtract polynomials we need to learn a trick. The trick to
adding and subtracting polynomials is to add or subtract things that look alike. In
other words we need to “combine like terms”. As a class we will fill out the
following chart:

Like and Unlike Term
4x	3	Unlike, no variables in 3
4x	3y	Unlike, different variables
4x	3x²	Unlike, different degrees
4x	3x	Like terms

As a class we will an example: (3x +2) (2x +5). I will show the class the example with
the algebra tiles, and then I will show the class how to do the problem like an addition
problem. 3x + 2

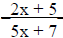
LESSON 1: Adding and Subtraction Polynomials

RECALL:

How do we solve 2³ ?

What about x³ ? Is it the same?

What is we put a number in front of the x? 4x³
NEW:
A. The 4 in the equation is called a
___________________________________________.
A ___________________________________ : is a number in front of an x that is
multiplied in with the x’s.

Example:

B. Polynomial:
“poly” means:
Example:

C.
• Monomial:
• Binomial:
• Trinomial:

When we have more than _______________________________ we do not have any
fancy names we simply call it a ____________________________.

D. Finding the degree of a polynomial.
When finding the degree of a polynomial we look for
_____________________________.
The degree of a polynomial is ___________________________________________.

Examples:

E. Adding and subtracting Polynomails

Represents _____________________

Represents ______________________

How do we represent x² + 5x + 6?

What about 2x² 3x + 5?

The Trick to adding and subtracting polynomials is:

Like and Unlike Terms
4x	3
4x	3y
4x	3 x²
4x	3x

Example:

Exercise 2
• I will pass out the student worksheet. I will tell students that they are able to use
either the algebra tiles or they can do each problem like a normal
addition/subtraction problem. Students will be able to work with a partner to
complete the worksheet as well as help each other. As students work I will
circulate the room to give assistance. I will give the students 15-20 minutes to
work.

(see student worksheet 1)

Exercise 3
• As a class we will go over the student worksheet. I will have students come up to
the board to show and explain what they did either using the algebra tiles or just
simply adding and subtracting. To make sure students understand polynomials, I
will ask for a few student volunteers to explain to me what a polynomial,
monomial, binomial, and trinomial are. I will ask the class if they have any
questions or problems with the new concept of adding and subtracting
polynomials. I will pass out the homework and explain it to the class.

(see homework sheet 1)

Directions: Represent each polynomial with algebra tiles. Draw a picture of your work.
Write a + for positive numbers, and – for negative numbers.

1. 2x + 3

2. x²+3x + 5

3. -3x² + 2x – 8

Directions: Combine the following polynomials. Draw a picture of your work.

1. (3x+ 7) + ( x-4)

2. (-2x + 4) + (6x+ 2)

3. (2x² –x+3) + (x²+3x-1)

4. (x² +2x-3) – (3 x² -4x-6)

Directions: Represent each polynomial with algebra tiles. Draw a picture of your work.
Write a + for positive numbers, and – for negative numbers.

1. 3 x² + 2x – 5
2. x² -5x +8
3. 8

Directions: Combine the following polynomials. Draw a picture of your work or show
your work.

4. (-x² + x – 1) +(4 x² + 2x – 5)

5. ( 3 x² + 5x – 6 ) + ( -2 x² – 3x – 6)

6. (2 x² – x -1) + ( -2 x² +x +1)

7. (5 x² -3x+4) + (- ² + 3x - 2)

8. (2 x² +5) - ( -x² + 3x)

9. (x² + 4) - ( 2 x² + x)

10. ( -x²+ 3x + 7)+ ( x² – 7)

Day 2: Exponents

Lesson Summary

Students will be able to identify and explain an exponent.

Students will be able to combine equations due to exponent rules.

Students will be able to identify exponent rules.

Students will be able to perform different operations of polynomials with different
exponents.

Materials:

Teacher:

• Overhead projector
• Notes
• Computer with projection device

Student

• Student note sheet
• Computer
• pencil

NYSED Standards addressed in this lesson:

A.N.6
Evaluating expressions involving factorial(s), absolute value(s), and exponential
expression(s)

A.A.12
Multiplication/Division of monomials expressions with a common base using the
properties of exponents (integral exponents only)

Description of the Lesson
During the lesson I will have an overhead transparency with the notes while the students
will have a copy of the notes. Students will fill in the areas of the notes as we go through
the lesson.

Exercise 1

• I will write the word exponent on the board. I will ask the students who can give
me the definition of an exponent? After taking a few responses I will give
students the correct definition. Exponent: A number or symbol, as 3 in (x + y)³,
placed to the right of and above another number, symbol , or expression, denoting
the power to which that number, symbol, or expression is to be raised. Also called
power
I will explain to the students the example of n to the fourth power means
n⁴= n x n x n x n

• I will tell the students that we are now going to learn 6 rules that will help us
understand exponents and the relationships between them. I will explain to the
students that it is important to learn exponent rules in order to continue our
education of polynomials.

• On the overhead I will write 3¹
I will ask the students how do you think we would figure this problem out? What
does the exponent mean? After taking a few student responses I will explain to the
students the rule. I will tell the students that this is the “rule of 1”. Any number
that is raised to the exponent (power) of 1 is equal to itself. Therefore 3¹= 3. I will
explain to the students how this makes sense, because the power shows how many
times the base is multiplied by itself. If it's only multiplied one time, then it's
logical that it equals itself.

Rule of 1

x¹=x

• On the board I will write 4² x 4³
I will ask the student do look at the exponents, what do we notice about them? I
will tell the students that since they are unlike we are unable to multiply them. We
have to learn a new rule! That rule is the “product rule”. I will explain to the
students that the “product” rule states that when multiplying powers if you have
the same bases, you add the exponents. Therefore for the problem 4² x 4³ you
add the exponents ( 2+3= 5). For our problem we then have
4² x 4³ = 4²⁺³ = 4⁵ = 4 x 4 x 4 x 4 x 4

I will explain to the students that adding the exponents is a short cut because you
could figure out the problem the long way which consists of:
4² = 4 x 4
4³ = 4 x 4 x 4

When you put them all together you get 4 x 4 x 4 x 4 x 4

Product Rule

a^m x aⁿ = a^m+n

• I will tell the students to look at the next problem: (5² )³
I will tell the students that for this problem we need to use the power rule. I will ask
the class if anyone has an idea how we might do the power rule. After taking a few
student responses I will demonstrate to the students how do to I with our example.
(5² )³= 5²*³=56

The “power rule” tells us to raise a power to a power. Therefore we multiply the
exponents.

Power Rule

(x^m)ⁿ= x^mn

• I will ask the students what about dividing. What if we have to divide two
numbers that have different exponents? Like 4⁵ / 4²
The “quotient rule” tells you that you are able to divide two powers with the same
base by subtracting the exponents. Therefore 4⁵ / 4² = 4^5-2=43

Quotient Rule

x^m / xⁿ= x^m-n

• I will tell the students that we already the 1 power, how about the 0 power. I will
tell the students that the “zero power” states that any nonzero number raised to the
power of 0 equals 1.

Zero Rule

X⁰=1

• I will tell that students that the last rule we are going to cover is the “negative
exponents” rule. I will tell the class that for this rule there are two parts.
A. 4^-2
B. 1/4^-2
For this rule I will show the students that any nonzero number raised to a negative
power equals its reciprocal raised to the opposite positive power.
Therefore:
A. 4^-2=1/4²
B. 1/4^-2=4²

Negative Exponents Rule	x^-2=1/x²
	1/x^-2=x²

• With the class we will review all the rules and put it a chart form.

Rule of 1	x¹=x
Product Rule	a^m x aⁿ = a^m+n
Power Rule	(x^m)ⁿ= x^mn
Quotient Rule	x^m / xⁿ= x^m-n
Zero Rule	X⁰=1
Negative Exponents Rule	x^-2=1/x²
Negative Exponents Rule	1/x^-2=x²

Exercise 2
• I will tell the students that they are going to have the chance to practice using
these rules. I will have the linked already bookmarked on the computers for the
students to save time Crunch time activities are a webpage
that allows students to do many examples with the click of a button. I will
demonstrate to the class how to obtain the website and work the website using my
computer and overhead projection device. I will show the students how there are 4
pages that contain the different crunch time activities (parts 1-4). I will
demonstrate to the students that they can get to the different parts by clicking next
lesson and previous lesson.

I will tell the students that they are to explore the four crunch time activities. On
each they are to do at least three examples and record the problem and answer for
the three (three for each part/page) on a sheet of paper. I will let the students
know that after they do three of each part/page and have it recorded on a sheet of
paper, they can play around with the activities.

As the class is working I will circulate the room and assist those who need it. I
will give the students 15-20 minutes to work.

Exercise 3

• When the class comes back together, I will ask some of the students to share some
of their examples and answers with the rest of the class. When the student comes
up to share their problems, I will ask them to explain to the class how they did the
problem as if they are teaching it to the rest of the class.

• I will ask the students how we would do the following problem:
2(x²) ⁴(w³) ⁶(x⁷) ² w
I will tell the students that for problems like these they will have to use more than
one rule. Therefore, they should break up problem and do it in pieces. As a class
we will figure out the problem.

• I will pass out the homework to the class and explain it. I will let the students
know that they are going to be doing problems like they one we just did, where
you have to incorporate more than one of the rules. I will tell the students to hand
in the work they did during independent work time. This way I can make sure the
students were working and not just fooling around.

Lesson 2: Exponents

A. What is an Exponent?

Example:

B. Let’s learn about the six important rules exponents! In the space provided
you can write the rule and examples.

1. Rule of 1 :

2. Product Rule:

3. Power Rule:

4. Quotient Rule:

5. Zero Rule

6. Negative Exponent Rule:

A.

B.

Let’s make a chart now to organize our rules and make it easy to find them!

Exponent Rules
Rule of 1
Product Rule
Power Rule
Quotient Rule
Zero Rule
Negative Exponent Rule

Directions: Using the multiple exponent rules simplify the equations.

1. 15052¹=

2. 3508⁰=

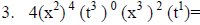
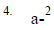
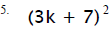
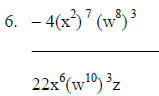
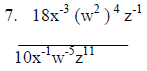
Day 3: Multiplying Polynomials

Lesson Summary

Students will be able to multiply polynomials using the distributive property, FOIL
method, and algebra tiles.

Materials:

Teacher:

• Overhead projector
• Notes
• Computer with projection device

Student

• Student note sheet
• Computer
• pencil

NYSED Standards addressed in this lesson:

A.A.13
Add, subtract, and multiply monomials and polynomials

A.A.12
Multiplication/Division of monomials expressions with a common base using the
properties of exponents (integral exponents only)

Description of the Lesson

During the lesson I will have an overhead transparency with the notes while the students
will have a copy of the notes. Students will fill in the areas of the notes as we go through
the lesson.

Exercise 1
• I will ask the class to think and try to recall the distributive property. I will ask for
a few student volunteers to show how we would represent the distributive
property. After taking a few student responses I will give the class the formal
representation: a(b+c) = ab + ac

I will tell the students we can check this by doing a simple problem:

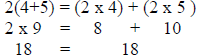
• I will tell the class that we are now going to try this with x values. I will show the
following example: 3x² (x+5). I will tell the students to take a few minutes and
try to figure out the problem. I will ask for a student volunteer to come to the
board and show how they figured out the problem. If no one figured it out I will
demonstrate the problem to the class.

3x² (x+5) = 3x² (x) + 3x² (5)

I will make sure to point out to the students that this is where are exponent rules
come in handy. I will tell the students that for now if they want to pull out their
not sheet that has the exponent rules on it they can.

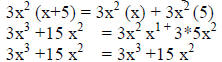
• I will now introduce the FOIL method to the class. I will tell the students that the
FOIL method: is used for multiplying two binomials. I will recall the word
binomials by asking the class what a binomial is. I will explain to the class that
the FOIL method is an easy way to do the distributive property twice. I will break
down the FOIL method with the class to show them how it works.

I will write the example:
(2x+3)(x-5)
I will tell the class we are going to do this example using the FOIL method:

1. First : (multiply the first term of each binomial together)
(2x)(x)= 2x²

2. Outer: (multiply the two outside terms together)
(2x)(-5)= -10x

3. Inner: ( multiply the two inside terms together)
(3)(x)= 3x

4. Last: (multiply the last terms of each binomial together)
(3)(-5)= -15

Now that we have all of our terms, we add them together in descending order of the
power of variable. Then we get:
(2x+3)(x-5) = 2x²-7x-15

I will give the class another example to practice with. (2x+3)(4x²–x+5).
I will tell the class that although this looks more difficult and messier, it isn’t, that they
just need to take their time while working. I will give the class a few minutes to work on
the problem before we go over it. I will make sure to point out that when doing this
problem you should first match up the 2x to every variable in the second ( ), and then
match up the 3. I will ask for a student to come up and demonstrate what they did.
(2x+3)(4x²–x+5) = 8x³ -12x² + 10x + 12x² – 3x + 15. I will make sure the students
combine like terms so that they get: 8x³+10 x²+7x + 15.

• I will tell the students that another way to multiply polynomials is to multiply then
vertically like you would a normal multiplication problem that uses numbers.

I will have students recall a multiplication problem with numbers, such as:

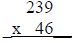
I will tell students that when multiplying polynomials you stack them the same
way. We will use our previous example from the FOIL problem to demonstrate.

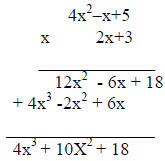
I will demonstrate the example to the class, making sure to point out that when
you multiply the terms, you are to stack the like terms together. This is called the
“stacking method”.

Exercise 2

• I will ask the students if they remember how we used are algebra tiles to add and
subtract polynomials. I will tell the students that today we are going to use an
online program that allows us to use the algebra tiles to multiply polynomials.
I will show the students how to use the algebra tiles (I will aware them that what
they do with he online program can also be done with their cardboard algebra
tiles). Students will use the National Library of Virtual Manipulatives, Algebra
tiles activity to help assist them with a student worksheet. The Algebra Tiles
activity helps you visualize multiplying algebraic expressions using tiles. I will
tell the students to remember what our algebra tile represented. As a class we will
do the following example: ( x+1)(x+2)

	X + 1
X + 2

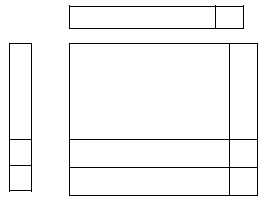
Using the algebra tiles, I will help to show the students that ( x+1)(x+2) = x² + 3x + 2

I will tell them that they are to go to algebra, under 6-8 and click it and then choose
algebra tiles. I will demonstrate this with my computer and overhead projector. I will pass
out the student worksheet and tell the students that using the algebra tiles and other
methods we discussed you are to complete the worksheet. I will give the students about
15 minutes to work.

Exercise 3

• As a class we will go over the worksheet. I will have students come up to the front
and use my computer to demonstrate to the class how to use algebra tiles to
multiply polynomials.
• I will pass out the homework sheet and discuss it with the class.

Lesson 3: Multiplying Polynomials

A. Recall: Distributive Property

Examples:

B. FOIL METHOD

Definition

• FOIL:
Let’s break it down

• F _______________________________________
• O _______________________________________
• I ________________________________________
• L _______________________________________

Examples:

(2x+3)(x-5)

(2x+3)(4x² –x+5)

C. Stacking Method:

Recall:

Using Polynomials:

Directions: Use the National Library of Virtual Manipulatives; Algebra Tiles activity to
help multiply the following polynomials. Draw a picture to show your work. Write your
final answer on the line provided.

1. (x-3)(X-5)

ANSWER:______________________________________
2. (3x +1)(x-2)

ANSWER:_____________________________________
3. (2x-2)(x+1)

ANSWER:__________________________________

4. (x+6)(x-3)
ANSWER:______________________________________
Use the FOIL method to answer the following questions

5. (x+8)(x-2)

6. (x-3)(x²+2x+1)

Directions: Multiply the following Polynomials. Draw a picture of your work.

1. (x+3)(x-4)

2. (3x+1)(x+2)

3. (2x-3)(3x+4)

Directions: Use the FOIL method to multiply the following polynomials. Show your
work.

4. (4x-7)(x-3)

5. (2x-1)(x² +2x+1)

Directions: Use the Stack Method to multiply the following polynomial. Show your
work.

6. (5x² -3x +6) (2x+1)

DAY 4: Dividing Polynomials

Lesson Summary

Students will be able to divide polynomials by monomials, binomials, trinomials, and
other polynomials.
Materials:

Teacher:

Describe what materials the teacher will need.

• Overheard projector
• Note Sheet Transparency

Student

• Student note sheet
• Pencil
• worksheet

NYSED Standards addressed in this lesson:

A.N.6
Evaluating expressions involving factorial(s), absolute value(s), and exponential
expression(s)

A.A..14
Divide a polynomial by a monomial or binomial (quotient has no remainder)

Description of the Lesson

Exercise 1
During the lesson I will have an overhead transparency with the notes while the students
will have a copy of the notes. Students will fill in the areas of the notes as we go through
the lesson.

• I will write the following words; monomial, binomial, trinomial. I will review the
terms with the students. The students should now have prior knowledge of these
terms and should be able recollect the definitions of them.

• I will first show the students how to divide a polynomial by a monomial.
I will use the following example: (18x⁴ – 10x² + 6x⁷ ) / 2x²
I will make it clear to the students that since there is only one term in the
denominator , we can break things up. Therefore our problem will look as follows:

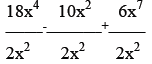
Now all we have to do is reduce . I will ask the students to recall our
exponent rules. I will ask for a student to raise their hand and tell me what the rule
we are going to use here is. I will remind the students that we are going to subtract
the exponents:

9x² – 5 + 3x⁷

• I will tell the students that we are going to now look at long division. I will
point out to the students that long division is done when you divide a
polynomial by a binomial, trinomial, or another polynomial. I will tell the
students to think of 78921/3. I will tell them to remember how they would set
up this problem, and what process they would take when figuring out an
answer.

I will tell the students that long division with polynomials is the same way,
you just have to deal with all the x junk!

I will model the following problem with the class:
(4x² + 6x+ 1) (2x-1)

I will tell the students we are going to follow six steps for long division. I will
tell them that for now they are to write out the six steps but eventually they
will not have to.

Step 1: Set up the Long Division

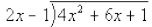
Step 2: Divide 1st term of divisor by first term of dividend to get first term of
the quotient.

The quotient (answer) is written above the division box.

Make sure that you line up the first term of the quotient with the
term of the dividend that has the same degree

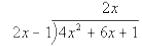
Step 3: Take the term found in step 1 and multiply it times the divisor.

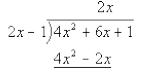
Step 4: Subtract this from the line above.
Make sure that you subtract EVERY term found in step 3, not just
the first one.

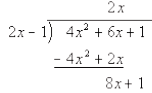
Step 5: REPEAT UNTIL DONE

Step 6: Write out the answer.
Your answer is the quotient that you ended up with on the top of
the division box.

If you have a remainder, write it over the divisor in your final
answer.

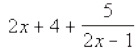
Exercise 2
I will tell the students that I know this may be a hard concept to grasp. Therefore, I am
going to give them a lot of independent work time to experiment with this concept and
have some hands on activity.

This website allows you to divide binomials and trinomials by monomials. The website
allows you to do this by playing a game and having to pick the right multiple choices.
As students are working at their computer, I will circulate the room giving my assistance
to the students. This will be a way for me to assess the students and see how well they
understand the concept. I will give the students about 20 minutes to work.

Exercise 3
• After students are done working, I will bring the class back together. I will get
the students input of how they felt about the game and how comfortable they
feel about dividing polynomials.

• I will tell students we are going to now work on a long division problem.
I will write the following problem on the board: (6x² +x-1) /(2x+1).
I will give the students a few minutes to independently work on the problem.
When I bring the class back together I will call several different students up to
the board to perform the various steps it takes to complete a long division
problem.

• I will pass out the homework and explain it to the class. I will ask the students
if they have any questions dealing with the topic or a previous related topic.

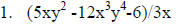
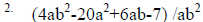
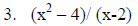
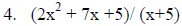
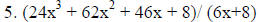
Lesson 4: Dividing Polynomials

RECALL:

• Monomial:

• Binomial:

• Trinomial

A. Dividing a Polynomial by a Monomial:

B. LONG DIVISION: Dividing a Polynomial by a Binomial, Trinomial, and other
Polynomials

SIX IMPORTANT STEPS:
1.
2.
3.
4.
5.
6.

DAY 5: Factoring Polynomials

Lesson Summary

Students will be able to identify and factor binomials that are the differences of squares
when given examples.

Students will be able to identify and factor perfect square trinomials when given
examples.

Students will be able to identify and factor difference of two cubes when given examples.

Materials:

Teacher:

Describe what materials the teacher will need.
• Overheard projector
• Note Sheet Transparency

Student

• Student note sheet
• Pencil
• worksheet

NYSED Standards addressed in this lesson:

A.N.6
Evaluating expressions involving factorial(s), absolute value(s), and exponential
expression(s)

A.A.13
Add, subtract, and multiply monomials and polynomials
Description of the Lesson

Exercise 1

• I will ask to students to think about the word factor.
3 x 2 = 6 What are the factors in this problem? I will review with the students that
the answer is 3 and 2.

What about 3x³y²v? What are the factors here? With the class I will conclude that
3,x,y,v are all factors.

• If we have the problem 2x + 2y what can we “take out” Looking at the problem I
will help point out to the students that we can take out the 2. 2 (x+y)
I will ask the students, What about 5x² + 10 x? I will take a student volunteer and
together we will conclude that you can take out 5x. Therefore you will get
5x(x+2).

I will tell the students that they KEY thing to remember that what you are looking
for is something that has to be in every term.

• Next I will talk about factoring trinomials. I will tell the students that in order to
factor trinomials we need to remember FOIL. With the class we will review the
concept of FOIL.

• I will write the following example on the board x² - 4x – 45.
I will tell the students that the first thing we need to remember FOIL and
remember the inner and outer guys. We first want to put down the x’s.
( x ) ( x )

Next we want to put down our outer numbers. For right now I will give them to
the student.

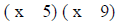
Next we have to figure out the signs . To do this look at the last term in the second
( ). – 45.
Here are the rules for signs
IF the last term is :
- ( then you must have a ( +) and a (-)
+ (you can either have (+)(+) or (-)(-)

Since we know we have a + and - sign, we just have to figure out where in the
problem they go. To do this we look at the second term in the first (). After
looking at the problem I will explain to the problem how the answer is:
(x-9)(x + 5)

I will continue to do examples with the students so they can grasp the concept. I
will slowly start to take away information I originally gave them. ( giving them
the last term in each equation).

As a class we will go over some of the special factoring rules:
1. differences of two squares:

(x² – b² ) = (x-b)(x+b) example: (x² –9)= (x-3)(x+3)

2. differences of two cubes: ( x³ –a³ )= (x – a) (x² –ax-a²)

3. the sum of two cubes: (x³ +a³ )= (x +a) (x² –ax+a²)

I will go over with the students the following:

RULES you should always follow when factoring:

1. always see if you can factor something out of the term
2. If it has two terms, most likely it has one of the special rules
3. if it has three terms, we follow the rules for factoring polynomials
4. if it has four terms we have to factor by grouping.

Exercise 2

I will tell the students that they are going to be able to have time to work in groups of 3-4
and work on various factoring problems. As students work I will circulate the room. I
will tell the students whatever they do not finish they are to finish for homework. We will
have about 10-15 minutes to work on this assignment.

Exercise 3

For overall assessment for the week I will have students take a mini quiz that covers all
of the topics this week. Students will have to use all their knowledge they learned this
week to take the quiz.

Lesson 5: Factoring Polynomials

A. Factor:

Recall:

New:

The KEY thing to remember is
___________________________________________.

B. Factoring Trinomials:

Let’s talk about the signs:
- _________________________________
+ _________________________________

C. Three SPECIAL Factoring Rules:

1. Differences of two squares:

2. Difference of two cubes:

3. Sum of two subes:

D. Four Rules You Should Always Follow When Factoring:
1.
2.
3.

1. Factor: x²-9

2. Factor: a²-36

3. Factor: 9y²-81

4. Factor: 16y⁶-25x²

5. Factor: a²- (1/9)

6. Factor: 5-5x²y⁶

7. Factor: 16yx⁴-81y

8. Factor: x²-10x+25.

9. Factor: 16y²+56y+49

10. Factor: 2x²-12xy+18y²

11. Factor: -4y²-144y⁸+48y⁵

12. Factor: x³-27

13. Factor: 125x³+y³

14. Factor: 128y⁷-250yx⁶

15. Factor: z³+27

16. Factor: 64y³+1

17. Factor: 5x³-40z³

18. Factor: 2y⁴-128y

1. What is the degree of the following polynomial?
16y⁶-25x²

2. Use algebra tiles to represent the following polynomial. 2x² + 3x + 8

3. Combine the following polynomials. Draw a picture or show your work.
(-x² + x – 1) +(4 x² + 2x – 5)

4. Using multiple exponent rules simplify the equation:

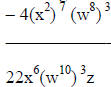
5. Use the FOIL method to multiply the following polynomial: (3x-2)(2x+4)

6. Use the Stack method to multiply the following polynomial:
(5x² -3x +6) (2x+1)

7. Using long division multiply the follow polynomial: (4x² + 6x+ 1) (2x-1)

8.Factor the following polynomial: (x² -9)

9. Factor the following polynomial: 2y⁴-128y