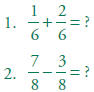The California Mathematics Content Standards

1.0 Students understand the place value of whole numbers:

1.1 Count, read, and write whole numbers to 10,000.

What is the smallest whole number you can make using the digits 4, 3, 9,
and 1? Use each digit exactly once (Adapted from TIMSS gr. 4, T-2).

1.2 Compare and order whole numbers to 10,000.

Identify the place value for each digit in numbers to 10,000.

1.4 Round off numbers to 10,000 to the nearest ten, hundred, and thousand.

Use expanded notation to represent numbers (e.g., 3,206 = 3,000 + 200 + 6).

True or false?

3,102 × 3 = 9,000 + 300 + 6 

2.0 Students calculate and solve problems involving addition, subtraction,
multiplication, and division:

Find the sum or difference of two whole numbers between 0 and 10,000.

1. 591 + 87 = ?

2. 1,283 + 6,074 = ?

3. 3,215 - 2,876 = ?

To prepare for recycling on Monday, Michael collected all the bottles in
the house. He found 5 dark green ones, 8 clear ones with liquid still in them,
11 brown ones that used to hold root beer , 2 still with the cap on from his
parents’ cooking needs, and 4 more that were oversized. How many bottles
did Michael collect? (This problem also supports Mathematical Reasoning
Standard 1.1.)

Memorize to automaticity the multiplication table for numbers between
1 and 10.

Use the inverse relationship of multiplication and division to compute
and check results.

Solve simple problems involving multiplication of multidigit numbers by
one-digit numbers (3,671 × 3 = __).

2.5 Solve division problems in which a multidigit number is evenly divided by
a one-digit number (135 ÷ 5 = __).

2.6 Understand the special properties of 0 and 1 in multiplication and division.

True or false?

1. 24 × 0 = 24

2. 19 ÷ 1 = 19

3. 63 × 1 = 63

4. 0 ÷ 0 = 1

2.7 Determine the unit cost when given the total cost and number of units.

2.8 Solve problems that require two or more of the skills mentioned above.

A price list in a store states: pen sets, $3; magnets, $4; sticker sets, $6.
How much would it cost to buy 5 pen sets, 7 magnets, and 8 sticker sets?

A tree was planted 54 years before 1961. How old is the tree in 1998?

A class of 73 students go on a field trip. The school hires vans, each of
which can seat a maximum of 10 students. The school policy is to seat as
many students as possible in a van before using the next one. How many
vans are needed?

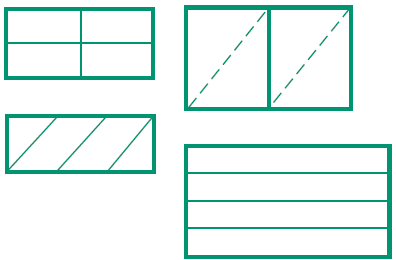
3.0 Students understand the relationship between whole numbers, simple fractions,
and decimals:

3.1 Compare fractions represented by drawings or concrete materials to show
equivalency and to add and subtract simple fractions in context (e.g., 1/2 of a
pizza is the same amount as 2/4 of another pizza that is the same size; show
that 3/8 is larger than 1/4).

Which is longer: 1/3 of a foot or 5 inches? 2/3 of a foot or 9 inches?

Which rectangle is NOT divided into four equal parts? (Adapted from
TIMSS gr. 4, K-8)

Add and subtract simple fractions (e.g., determine that 1/8 + 3/8 is the same
as 1/2).

Find the values:

Solve problems involving addition, subtraction, multiplication, and division
of money amounts in decimal notation and multiply and divide money
amounts in decimal notation by using whole-number multipliers and
divisors.

Pedro bought 5 pens, 2 erasers and 2 boxes of crayons. The pens cost
65 cents each, the erasers 25 cents each, and a box of crayons $1.10.
The prices include tax, and Pedro paid with a ten-dollar bill. How much
change did he get back?

3.4 Know and understand that fractions and decimals are two different representations
of the same concept (e.g., 50 cents is 1/2 of a dollar, 75 cents is 3/4 of a
dollar).
 

The symbol
identifies the key
standards for
grade three.

1.0 Students select appropriate symbols, operations, and properties to represent,
describe, simplify, and solve simple number relationships:

Represent relationships of quantities in the form of mathematical expressions,
equations, or inequalitie

1.2 Solve problems involving numeric equations or inequalities .

1.3 Select appropriate operational and relational symbols to make an expression
true (e.g., if 4 __ 3 = 12, what operational symbol goes in the blank?).

1.4 Express simple unit conversions in symbolic form
(e.g., __ inches = __ feet × 12).

If number of feet = number of yards × 3, and number of inches =
number of feet × 12, how many inches are there in 4 yards?

1.5 Recognize and use the commutative and associative properties of multiplication
(e.g., if 5 × 7 = 35, then what is 7 × 5? and if 5 × 7 × 3 = 105, then
what is 7 × 3 × 5?).

2.0 Students represent simple functional relationships:

Solve simple problems involving a functional relationship between two
quantities (e.g., find the total cost of multiple items given the cost per unit).

John wants to buy a dozen pencils. One store offers pencils at 6 for $1.
Another offers them at 4 for 65 cents. Yet another sells pencils at 15 cents
each. Where should John purchase his pencils in order to save the most
money?

2.2 Extend and recognize a linear pattern by its rules (e.g., the number of legs on
a given number of horses may be calculated by counting by 4s or by multiplying
the number of horses by 4).

Here is the beginning of a pattern of tiles. Assuming that the pattern
continues linearly , how many tiles will be in the sixth figure?
(Adapted from TIMSS gr. 4, K–6)

1.0 Students choose and use appropriate units and measurement tools to quantify
the properties of objects:

1.1 Choose the appropriate tools and units (metric and U.S.) and estimate and
measure the length, liquid volume, and weight/mass of given objects

Estimate or determine the area and volume of solid figures by covering them
with squares or by counting the number of cubes that would fill them.

Find the perimeter of a polygon with integer sides.

1.4 Carry out simple unit conversions within a system of measurement
(e.g., centimeters and meters, hours and minutes).

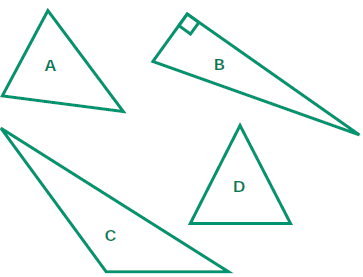
2.0 Students describe and compare the attributes of plane and solid geometric
figures and use their understanding to show relationships and solve problems:

Identify, describe, and classify polygons (including pentagons, hexagons, and
octagons).

Identify attributes of triangles (e.g., two equal sides for the isosceles triangle,
three equal sides for the equilateral triangle, right angle for the right triangle).

Identify attributes of quadrilaterals (e.g., parallel sides for the parallelogram,
right angles for the rectangle, equal sides and right angles for the square).

2.4 Identify right angles in geometric figures or in appropriate objects and
determine whether other angles are greater or less than a right angle.

Which of the following triangles include an angle that is greater than
a right angle?

2.5 Identify, describe, and classify common three-dimensional geometric objects
(e.g., cube, rectangular solid, sphere, prism, pyramid, cone, cylinder).

2.6 Identify common solid objects that are the components needed to make a
more complex solid object.
 

1.0 Students conduct simple probability experiments by determining the number
of possible outcomes and make simple predictions:

1.1 Identify whether common events are certain, likely, unlikely , or improbable.

Are any of the following certain, likely, unlikely, or impossible?

1. Take two cubes each with the numbers 1, 2, 3, 4, 5, 6 written on its six
faces. Throw them at random, and the sum of the numbers on the top
faces is 12.

2. It snows on New Year’s day.

3. A baseball game is played somewhere in this country on any Sunday
in July.

4. It is sunny in June.

5. Pick any two one-digit numbers, and their sum is 17.

Record the possible outcomes for a simple event (e.g., tossing a coin) and
systematically keep track of the outcomes when the event is repeated many
times.

Summarize and display the results of probability experiments in a clear and
organized way (e.g., use a bar graph or a line plot).

1.4 Use the results of probability experiments to predict future events (e.g., use a
line plot to predict the temperature forecast for the next day).
 

1.0 Students make decisions about how to approach problems:

1.1 Analyze problems by identifying relationships, distinguishing relevant from
irrelevant information, sequencing and prioritizing information, and observing
patterns.

1.2 Determine when and how to break a problem into simpler parts.

2.0 Students use strategies, skills, and concepts in finding solutions:

2.1 Use estimation to verify the reasonableness of calculated results.

Prove or disprove a classmate’s claim that 49 is more than 21 because
9 is more than 1.

2.2 Apply strategies and results from simpler problems to more complex
problems.

2.3 Use a variety of methods, such as words, numbers, symbols, charts, graphs,
tables, diagrams, and models, to explain mathematical reasoning.

2.4 Express the solution clearly and logically by using the appropriate mathematical
notation and terms and clear language; support solutions with
evidence in both verbal and symbolic work.

2.5 Indicate the relative advantages of exact and approximate solutions to
problems and give answers to a specified degree of accuracy.

2.6 Make precise calculations and check the validity of the results from the
context of the problem.

3.0 Students move beyond a particular problem by generalizing to other
situations:

3.1 Evaluate the reasonableness of the solution in the context of the original
situation.

3.2 Note the method of deriving the solution and demonstrate a conceptual
understanding of the derivation by solving similar problems.

3.3 Develop generalizations of the results obtained and apply them in other
circumstances.