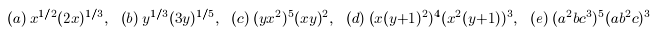Vital Errors in Math 112
There are two very common errors that Math 112 students make. These mistakes
make Math 112
instructors very sad and are given great weight in the grading of exams. Making
these mistakes
will cause you to earn at best half-credit—and of ten zero credit —in an other
wise correctly worked
problem. When grading, instructors often mark vital errors by VE.
The first kind of vital error is to distribute a power across a sum or a
difference:

Example 1:
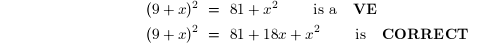
Example 2:
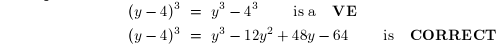
Example 3:
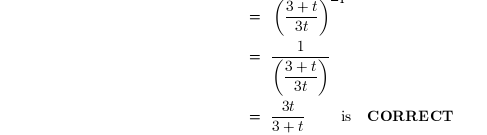
Example 4:
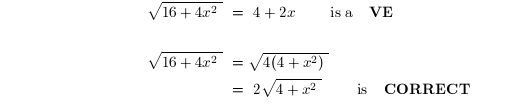
NOTE: As seen in examples 3 and 4, it is CORRECT to apply powers to the
individual parts
of a product or quotient . For example:

are all CORRECT .
The second kind of vital error in Math 112 occurs when cancelling from the
numerator and denominator of a fraction . It is correct to cancel factors that
are common
to both the numerator and denominator, however it is incorrect to cancel
something a term that
appears in a sum or difference in the numerator :
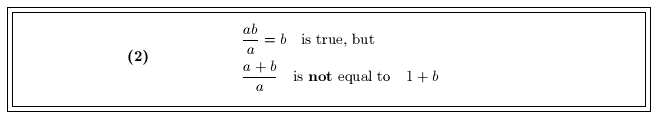
Example 1: The following are all incorrect.
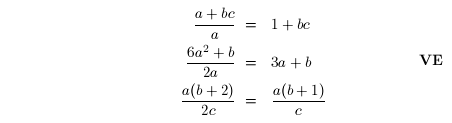
Example 2: The following are correct:
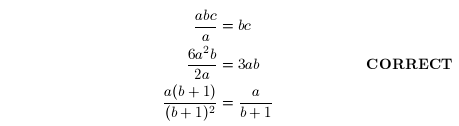
Example 3:
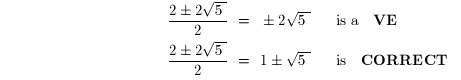
Radicals and Rational Exponents
(Relates to text sections B.2 and B.3)
Practice Problems:
1. Rewrite using fractional exponents . Simplify when possible.
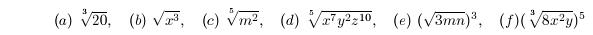
2. Rewrite using only positive exponents .
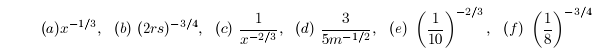
3. Simplify as much as possible.
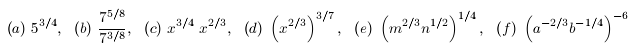
4. Simplify.
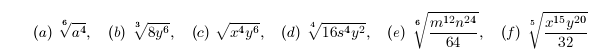
6. Perform the indicated operation and simplify.
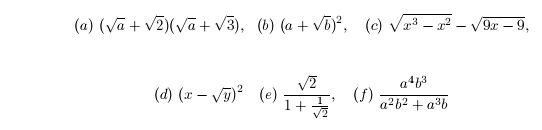
Working With Fractions
(Relates to text section B.5)
In this course, there are two basic types of problems that
involve fractions. It is important to
distinguish between them, because they are handled differently . In the first
type, you are asked
to simplify a fractional expression. In the second type, you are asked to solve
a fractional
equation. The two methods are described below with examples.
1. Simplify the expression :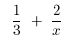
Solution : You are asked to combine the two fractions. You need to write the two
fractions
over a single common denominator. The least common denominator, l.c.d., of the
two fractions
is 3x. Thus,
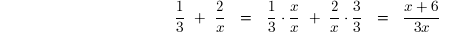
2. Solve this equation for x: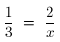
Solution: You are asked to solve the equation for x. That is, find all values of
x that make
the equation true. The l.c.d. of the two fractions is 3x. We can multiply both
sides of the
equation by 3x and get an equivalent equation (except for the case where 3x = 0,
see page 71
of your text):

3. Simplify: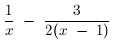
Solution: Write over the single l.c.d.: 2x(x-1).
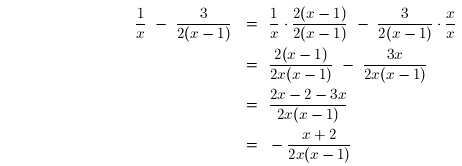
4. Solve: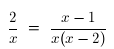
Solution: Multiply both sides of the equation by the l.c.d.: x(x-2).
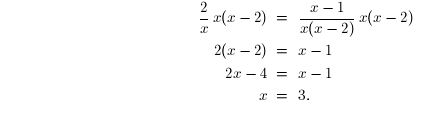
| Prev | Next |