Algebra and Trigonometry Credit Exam
The following is a list of competencies addressed on the
exam.
The student will be able to:
1. Classify real numbers as rational , irrational, integer, and/or non-integer
values.
2. Identify real number properties such as commutativity, associativity,
distributive
law, identities, and inverses.
3. Graph points and intervals of points on the real number line.
4. Simplify real number expressions using order of operations .
5. Simplify exponential expressions using rules for exponents .
6. Express numbers in scientific notation.
7. Simplify radical expressions using rules for radicals.
8. Identify the terms and degree of a polynomial.
9. Add, subtract, and multiply polynomials .
10. Factor algebraic expressions using such techniques as common factoring,
factoring by grouping, difference of squares, difference of cubes , sum of cubes,
and trial and error techniques for trinomials.
11. Simplify, multiply, divide, add, and subtract rational algebraic
expressions.
12. Solve linear equations.
13. Solve quadratic equations using such techniques as factoring, completing the
square, and quadratic formula.
14. Construct and use a linear model to solve an application problem.
15. Construct and use a quadratic model to solve an application problem.
16. Solve linear, quadratic, rational, and absolute value inequalities.
17. Plot points in the Cartesian plane.
18. Find the distance between two points in the plane.
19. Find the midpoint of a line segment.
20. Find the x- and y- intercepts of the graph of an equation.
21. Write the equation of a circle in standard form and identify its center and
radius.
22. Determine the symmetry of a graph.
23. Determine the slope of a line passing through two points.
24. Use the point-slope formula to find the equation of a line.
25. Use the slope-intercept form of a line to determine its slope and
y-intercept.
26. Determine if lines are parallel or perpendicular using their slope.
27. Determine whether an expression represents a function using various
techniques,
including the Vertical Line Test.
28. Determine the domain and range of various functions.
29. Graph a variety of functions, including, linear, parabolic, cubic, square
root ,
piecewise, absolute value, and greatest integer.
30. Construct and use models to relate quantities that vary directly, inversely,
and/or
jointly.
31. Identify common transformations of functions such as vertical shifting,
horizontal
shifting, reflecting, vertical stretching and shrinking, and horizontal
stretching and
shrinking.
32. Use the concept of transformation to sketch functions.
33. Classify a function as even or odd.
34. Find the sum, difference, product, and quotient of functions and identify
their
domains.
35. Form the composition of functions and identify their domain.
36. Determine the inverse of a function, if appropriate.
37. Divide polynomials using techniques such as long division and synthetic
division.
38. Find the zeros of a polynomial function.
39. Add, subtract, multiply, and divide complex numbers and write the results in
standard form.
40. Find the domain of a rational function, sketch its graph, and determine
vertical
and horizontal asymptotes.
41. Determine the domain and range of an exponential function and sketch its
graph.
42. Use an exponential model to solve an application problem.
43. Determine the domain and range of a logarithmic function and sketch its
graph.
44. Use a logarithmic model to solve an application problem.
45. Use properties of logarithms to expand and evaluate expressions.
46. Solve exponential and logarithmic equations algebraically.
47. Convert between radian and degree mode.
48. Given the measure of an angle in standard position, determine its
corresponding
reference and coterminal angles.
49. Solve right triangles using the six trigonometric ratios.
50. Apply the arc length formula of a circle.
51. Apply the area formula for a sector of a circle.
52. Apply the arc length and area formulas (i.e. angular and linear velocity,
etc.)
53. Evaluate the six trigonometric functions (circular functions).
54. Determine the period, phase shift, amplitude (when applicable) of
trigonometric
functions.
55. Graph trigonometric functions.
56. Determine the domain and range of trigonometric functions.
57. Graph inverse trigonometric functions.
58. Determine the domain and range of inverse trigonometric functions.
59. Evaluate inverse trigonometric functions and compositions of trigonometric
functions.
60. Represent real-world situations (applications) using trigonometric
functions.
61. Prove trigonometric identities.
62. Determine zeros of trigonometric functions.
An excellent source to review before attempting the exam is Schaum’s Outline of
Precalculus by Fred Safier (1998, McGraw-Hill).
The format of the exam is multiple-choice. Here are some sample questions. These
sample questions are designed to give you an idea of the format of the exam. In
no way
is this an exhaustive list of the topics covered on the exam.
1. Factor the expression 6x2 +13x + 6
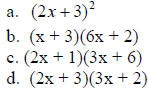
The correct answer is D.
2. Find the solution set for the nonlinear inequality x2 + x − 20 > 0
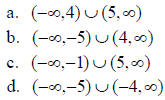
The correct answer is B.
3. Evaluate the expression 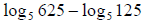
a. 1
b. 2
c. 3
d. -3
The correct answer is A.
4. Determine the domain of the function 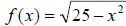
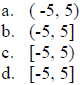
The correct answer is D.
5. If sec t = -2 and tan t > 0, then the csc t is
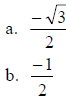
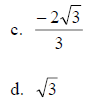
The correct answer is C.
6. The period of 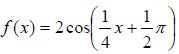 is
is
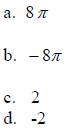
The correct answer is A.
| Prev | Next |