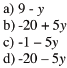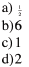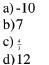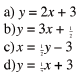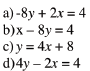Algebra Progress Monitoring
Session Overview
Introductions
Project AAIMS
Progress monitoring (PM)
Using PM data
Discussion
Introductions
Who am I?
• Project AAIMS Project Coordinator
• Former teacher
Who are you?
• Middle school/high school; general/special
education; classroom teacher/other role
Project AAIMS
Federally-funded 3 year research grant
U.S. Department of Education, Office of
Special Education Programs
Two primary activities
1. Describe algebra instruction for students with
and without disabilities (in both general and
special education settings); examine alignment
across settings
2. Develop and validate screening/progress
monitoring assessment tools for beginning
algebra classes
Project AAIMS Partner Districts
Ballard Junior/Senior High School
• Huxley, IA
Fort Dodge Senior High School
• Fort Dodge, IA
South Tama County Senior High School
• Tama, IA
Project AAIMS Research Plan
Series of studies to develop and
validate algebra progress monitoring
measures
• Static measures of performance
• ‘snapshot’
• Measures of student growth over time
• ‘movie’
• Utility of measures for teacher decision
making
Origins of Progress Monitoring
Special Education – 30 year history
Elementary
• Reading (DIBELS)
• Math
Secondary
• Project AAIMS
AYP Requirements (NCLB)
Progress Monitoring
Formative evaluation
Long- term measurement
Objective data to inform instructional
decision making
Graphed data to facilitate visual
interpretation
Repeated measurement using equivalent
brief tasks and standard conditions
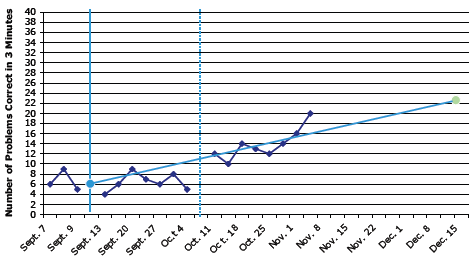
Mary's Math Progress
Characteristics of
Progress Monitoring Measures
Brief (5 to 7 minutes); consistent timing
Repeatable; constant difficulty
Easy to administer and score
Associated with other indicators of proficiency
(teacher ratings, grades, standardized test
scores)
Sensitive to changes in student performance
over time
5 Measures
Basic Skills
Algebra Foundations
Content Analysis
(constructed response)
Translations
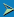Content Analysis-Multiple
Choice
Basic Skills
| Solve: 9 + a = 15 a = |
Solve: 10 – 6 = g g = |
| Evaluate: 12 + (– 8) + 3 |
Simplify : 9 – 4d + 2 + 7d |
| Simplify: 2x + 4 + 3x + 5 |
Simplify: 5(b – 3) – b |
| Solve: 12 – e = 4 e = |
Solve: q • 5 = 30 q = |
| Simplify: 4(3 + s) – 7 |
Evaluate: 8 – (– 6) – 4 |
| Simplify: b + b + 2b |
Simplify: 2 + w(w – 5) |
| Solve: b/6 = 12/18 b = |
Solve: 1 foot =12 inches 5 feet = ____ inches |
| Simplify: 7 – 3(f – 2) |
Simplify: 4 – 7b + 5(b – 1) |
| Evaluate: – 5 + (– 4) – 1 |
Simplify: s + 2s – 4s |
| Solve: 63 ÷ c = 9 c = |
Solve: x + 4 = 7 x = |
| Simplify: 2(s – 1) + 4 + 5s |
Simplify: – 5(q + 3) + 9 |
| Simplify: 8m – 9(m + 2) |
Evaluate: 9 + (– 3) – 8 |
Form A: Basic Skills
(in Algebra)
60 items; 5 minutes
Problems include solving simple (fact)
equations; combining like terms ; simplifying
expressions ; proportional reasoning
Hypothesis: these types of tasks may serve a
function in algebra that parallels the role of
decoding in reading comprehension: an
enabling skill that is necessary, but not
sufficient, to support more complex skills
Scoring: # of problems correct
Content Analysis - Multiple Choice
| Evaluate b2-a2 when a = 4 and b = 5 a)21 |
Rewrite this expression without parenthese : (-5)(4 - y)
|
Sole: 2t - 5 = 7
|
Sole: y/3 = 4
|
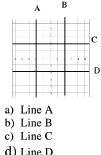
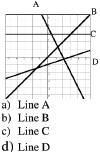
| Which line on the graph is y = 2?
|
Which line on the graph is y + 2x = 4?
|
Write the equation in slope - interept form: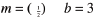 
|
Rewrite this equation in standard form using jnteger coefficients .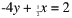 
|
Content Analysis-Multiple Choice
16 items; 7 minutes
Problems are sampled from 2 core concepts
from the first 8 chapters of text
Multiple choice
Scoring: 3 points per problem, -1 pt. penalty for
guessing; partial credit awarded for work shown
| Prev | Next |