Quadratic Equations
Completing the square ... again.
To make x2 + bx a perfect square, for example x2 − 6x,
1.
2.
A quadratic equation is an equation of the form
The solutions to a quadratic equation (and any polynomial equation
for that matter) are called .
Example. Solve the following quadratic equation:
• x2 − 2x − 3 = 0
• x2 − 2x − 4 = 0
The Quadratic Formula .
Example. Solve the equation 3x2 + 6bx + 4 = 0 (in terms of b)
The Quadratic Formula
Example. Solve the equation ax2 +bx+c = 0 (in terms of a, b, c).
Thus, the quadratic formula says that the solutions to
ax2+bx+c = 0
are
Example. Solve the following quadratic equations:
• x2 − 12x + 35 = 0
• x2 − 12x + 36 = 0
• x2 − 12x + 37 = 0
Therefore, the number of solutions you get to a quadratic equation
is either
The product and sum of roots.
Suppose the roots of x 2 + bx + c = 0 are
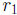and 
.
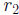Then x2 + bx + c =
So
Example. Find the roots of the following equations:
| • x2 − 2x − 3 = 0 | • x2 + x − 1 = 0 |
| Product of roots : | Product of roots : |
| Sum of roots : | Sum of roots : |
Example. Find the sum and product of the roots of the following
equations :
• x2 + 4x − 7 = 0
• 2x2 + 6x − 135 = 0
The Discriminant.
The discriminant of the quadratic equation ax2 + bx + c = 0 is
The discriminant can be used to tell how many solutions a quadratic
equation will have.
• If 
, then there are
solution (s).
• If , then there are
solution (s).
• If , then there are
solution(s).
Example. Find the number of real solutions for 2x2 − 3x − 1 = 0.
Example. Find a value of k which makes kx2 + 4x − 7 = 0
have
no real solutions .
| Prev | Next |