Linear difference equations with constant coeffici
Linear difference equations with constant coefficients
1. The forward shift operator
Many probability computations can be put in terms of recurrence relations that
have to be satisfied by successive
probabilities. The theory of difference equations is the appropriate tool for
solving such problems.
This theory looks a lot like the theory for linear differential equations with
constant coefficients.
In order to simplify notation we introduce the forward shift operator E , that
takes a term un and shifts the
index one step forward to un+1. We write
Eun = un+1
E2un = EEun = Eun+1 = Eun+2
...
Erun= un+r
The general linear difference equation of order r with constant coefficients is

where Φ(E) is a polynomial of degree r in E and where
we may assume that the coefficient of Er is 1.
2. Homogeneous difference equations
The simplest class of difference equations of the form (1) has f (n) = 0, that
is simply
Φ((E)un = 0.
These are called homogeneous equations.
When Φ(E) = (E−λ1)(E−λ2)...(E−λr) where the λi
are constants that are all distinct from each other,
one can prove that the most general solution to the homogeneous equation is
un =a1λ1n+ a2λ2n+...+arλrn
where a1, a2,..., ar are arbitrary constants.
WhenΦ(E) contains a repeated factor (E−λa )h, the
corresponding part of the general solution becomes
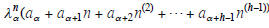
where n(k) = n(n−1)(n−2)...(n−k +1) = n!/(n−k)!.
In order to find the n'th term of a linear difference equation of order r, one
can of course start by r initial
values , and the solve recursively for any giv en n. Thus, if we want our
solution to satisfy certain initial conditions
we may first determine the general solution, and then (if possible) make it
satisfy the initial conditions.
There can be no more than r such initial conditions, but they need not (as when
we compute the solution
recursively) necessarily be conditions on u0,... , ur−1,
but can be on any set of r values.
Example 1. Solve un+2−un = 0.
The equation can be written in the form
(E2−1)un = 0
or
(E−1)(E +1)un = 0
The general solution is therefore
un = a(−1)n + b1n
where a, b, c are constants.
Example 2. Find the general solution to the equation
un+4 − 9un+3 + 30un+2
− 44un+1 + 24un = 0
and hence obtain the particular solution satisfying the conditions
u0 = 1, u1 = 5, u2 = 1, u3 = − 45.
The equation may be written in the form
(E4 − 9E3 + 30E2 − 44E + 24)un = 0
(E− 2)3(E − 3)un = 0.
The general solution is therefore
un = 2n(a + bn + cn(n− 1)) + d3n
where a, b, c, d are constants.
For the particular side conditions we have
u0 = a + d = 1,
u1 = 2a + 2b + 3d = 5
u2 = 4a + 8b + 8c + 9d = 1
u3 = 8a + 24b + 48c + 27d =− 45
whence a = 0, b = 1, c = − 2, d = 1, so the particular solution is
un = 2nn(3 − 2n) + 3n.
3. Non-homogeneous difference equations
When solving linear differential equations with constant coefficients one first
finds the general solution for
the homogeneous equation, and then adds any particular solution to the
non-homogeneous one. The same
recipe works in the case of difference equations, i.e. first find the general
solution to
Φ(E)un = 0
and a particular solution to
Φ(E) = f (n)
and add the two together for the general solution to the latter equation. Thus
to solve these more general
equations, the only new problem is to identify some particular solutions. We
will only give a few examples
here, not attempting to treat this problem in any generality.
(i) f (n) = kμ n, μ ≠ λi, i =
1, 2,... , r
In this case one can show that
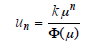
is a particular solution to Φ(E)un = kμ n. Let namely Φ(E)
=ΣaiEi. Then
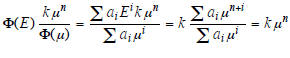
Example 3. The general solution of
un+2− 5un+1 + 6un = 3( 4n)
is un = a2n + b3n +
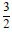 4n where a and b are arbitrary
constants.
4n where a and b are arbitrary
constants.
(ii) f (n) = kμ n, μ =λ i, λ
ia non-repeated factor of Φ(E)
In this case a particular solution is given by
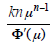
where Φ'(μ) denotes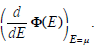
Example 4. The general solution of
un+2 − 5un+1 + 6un = 3( 2n)
is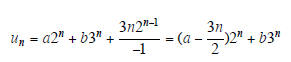
where a, b are arbitrary constants.
(iii) f (n) = kμ n, μ = λ i,λ
i a repeated factor of Φ(E)
Suppose now that (E − λ i is repeated h times in
Φ(E). Then
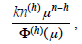
where n(k) = n(n − 1)...(n −
k +1), is a particular solution of the equation Φ(E) un = kμ
n.
Example 5. The general solution of the equation
(E−2)3(E−3)un = 5( 2n)
is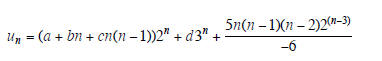
with a, b, c, d are arbitrary constants
(iv) f (n) is a polynomial in n
First write f as a polynomial in the factorial powers n(k), so
f (n) = a0 + a1n + a2n(2 )
+ ...
Now define the difference operator , by Δun = un+1−
un = (E−1) un. Using the symbolic relationship
E = 1 + Δ, we can re-express Φ(E)as Ψ(Δ).
Still arguing symbolically , a particular solution is obtained by
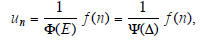
provided that we can make any sense out of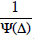 .The
way this will be done is by expanding
.The
way this will be done is by expanding 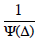 in
powers
in
powers
of , and using long division . The following rules are needed:
n(r) = rn(r−1)
Δ2n(r) = r(2 )n(r-2)
...
Δk n(r) = r(k)n(r-k)) for k≤r,
= 0 for k > r
and
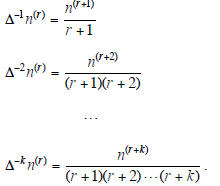
Example 6. Find a particular solution of the
equation
un+2-7un+1 +12un= 3n2 + 2n + 2.
First write 3n2 + 2n + 2 = 3n(2 ) + 5n(1 ) + 2
and E2 - 7E +12 = (2-Δ )( 3-Δ ). Thus we get
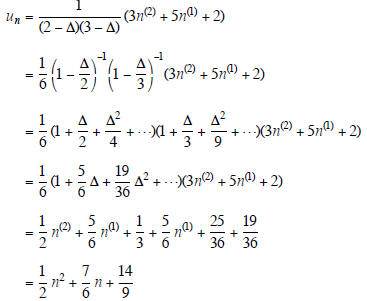
Example 7. Find a particular solution of the
equation
un+3 - 5un+2 + 7un+1 - 3un = n2
+ 4n +1.
The required solution is
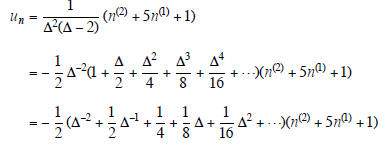
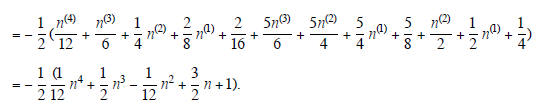
| Prev | Next |