Matrix, Vector Operations

Big-O

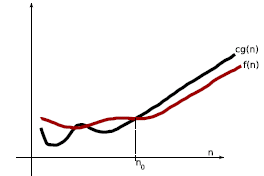
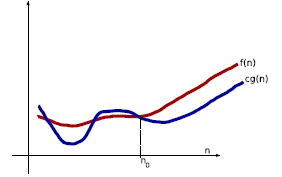
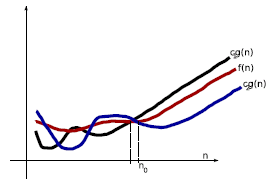
How to measure the impact of n on algorithmic cost?

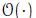
Let g(n) be a function of n. Then define

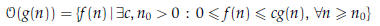
That is,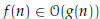 if there is a constant c such that 0 ≤  f (n) ≤ cg(n) is
satisfied.
• assume non-negative functions (otherwise add | . |) to the definitions
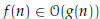• represents an asymptotic upper bound on f (n) up to a
constant
• example: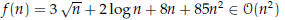

Big-Omega
asymptotic lower bound

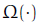
Let g(n) be a function of n. Then define

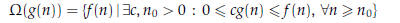
That is, if there is a constant c such that 0 ≤ cg(n) ≤ f (n) is
satisfied.

Big-Theta
asymptotic tight bound

Let g(n) be a function of n. Then define

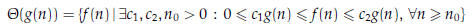
Equivalently,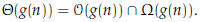

BLAS
Basic Linear Algebra Subprograms (BLAS) interface introduced APIs for
common linear algebra tasks
• Level 1: vector operations (dot products, vector norms, etc) e.g.

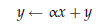
• Level 2: matrix-vector operations, e.g.

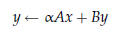
• Level 3: matrix-matrix operations, e.g.

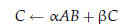
• optimized versions of the reference BLAS are used everyday: ATLAS, etc.

vec-vec, mat-vec, mat-mat

• inner product of u and v both [n × 1]

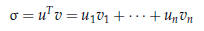
• → n multiplies, n - 1 additions
• → O(n) flops

• mat-vec of A ([n × n]) and u ([n × 1])

• → n² multiplies, n² additions
• → O(n²) flops

• mat-mat of A ([n × n]) and B ([n × n])

• → n³ multiplies, n³ additions
• → O(n³) flops

matlab test
four tests:
• matrix-matrix multiply
• inner product
• matrix-vector multiply
• n matrix-vector multiplies
order them ...fastest to slowest
testflop.m

Gaussian Elimination

• Solving Diagonal Systems
• Solving Triangular Systems
• Gaussian Elimination Without Pivoting
> Hand Calculations
>Cartoon Version
> The Algorithm
• Gaussian Elimination with Pivoting
> Row or Column Interchanges, or Both
> Implementation
• Solving Systems with the Backslash Operator

Solving Diagonal Systems
The system defined by

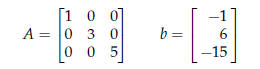
is equivalent to

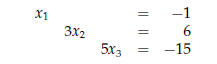
The solution is

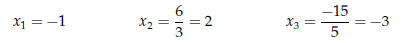
Listing 1: Diagonal System Solution

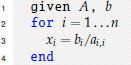
In Matlab:
1 >> A = ... % A is a diagonal matrix
2 >> b = ...
3 >> x = b./diag(A)

This is the only place where element-by- element division (. /) has anything to
do with solving linear systems of equations.

Operations?
Try...
Sketch out an operation count to solve a diagonal system of equations...

cheap!
one division n time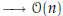s FLOPS

Triangular Systems
The generic lower and upper triangular matrices are

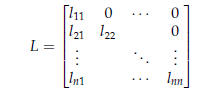
and

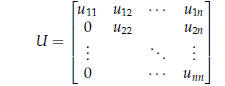
The triangular systems
Ly = b Ux = c

are easily solved by forward substitution and backward substitution,
respectively

Solving Triangular Systems

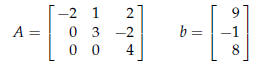
is equivalent to

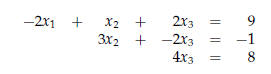
Solve in backward order (last equation is solved first)

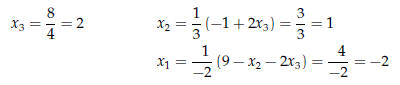
Solving for 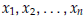for a lower triangular system is called forward
substitution.

Using forward or backward substitution is sometimes referred to as performing
a triangular solve.

Operations?

Try...
Sketch out an operation count to solve a triangular system of equations...

cheap!
• begin in the bottom corner: 1 div
• row -2: 1 mult, 1 add, 1 div, or 3 FLOPS
• row -3: 2 mult, 2 add, 1 div, or 5 FLOPS
• row -4: 3 mult, 3 add, 1 div, or 7 FLOPS
• ...
• row -j: about 2j FLOPS
Total FLOPS?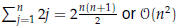 FLOPS