Solution Sets for Systems of Linear Equations
For a system of equations with r equations and k unknowns,
one can have a
number of different outcomes. For the sake of visualization, consider the case
of r equations in three variables. Geometrically, then, each of our equations
is the equation of a plane in three-dimensional space. To find solutions to
the system of equations, we look for the common intersection of the planes
(if an intersection exists). Here we have five different possibilities:
1. No solutions. Some of the equations are contradictory, so no solu-
tions exist.
2. Unique Solution. The planes have a unique point of intersection.
3. Line. The planes intersect in a common line; any point on that line
then gives a solution to the system of equations.
4. Plane. Perhaps you only had one equation to begin with, or else all
of the equations coincide geometrically. In this case, you have a plane
of solutions, with two free parameters.
5. All of R3. If you start with no information, then any point in R3 is a
solution. There are three free parameters.
In general, for systems of equations with k unknowns , there are k + 2
possibile outcomes, corresponding to the number of free parameters in the
solutions set, plus the possibility of no solutions. These types of solution
sets are hard to visualize, but luckily 'hyperplanes' behave like planes in R3
in many ways.
Non-Leading Variables
Variables that are not a pivot in the reduced row echelon form of a linear
system are free. Se set them equal to arbitrary parameters
.
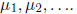Example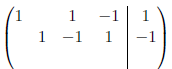 
Here,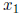 
and 
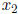are the pivot variables and
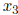and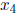 
are non-leading
variables, and thus free. The solutions are then of the form
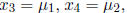
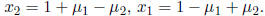
The preferred way to write a solution set is with set
notation. Let S be
the set of solutions to the system. Then:
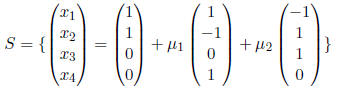
It's worth noting that if we knew how to multiply matrices
of any size,
we could write the previous system as MX = v, where
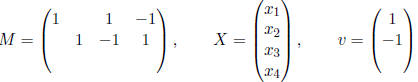
Given two vectors we can add them term -by-term:
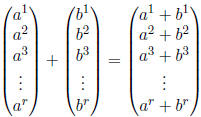
We can also multiply a vector by a scalar, like so:
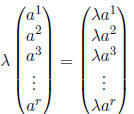
Then yet another way to write the solution set for the example is:
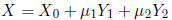
where
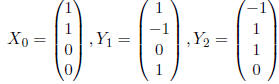
Definition Let X and Y by vectors and α and β be scalars. A
function f
is linear if
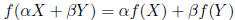
Eventually, we'll prove that matrix multiplication is linear. Then we will
know that:
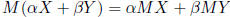
Then the two equations MX = v and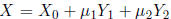 
together
say that:
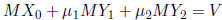
for any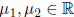 
.
Choosing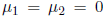 
, we obtain
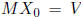. Given the particular
solution to the system, we can then deduce that
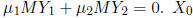
is an example of a particular solution to the system.
Setting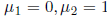
, and recalling the particular solution
,
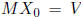we obtain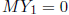 
.
Likewise, setting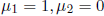 
, we obtain 
.
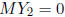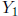and
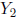are homogeneous solutions to the system.
Example Consider the linear system with the augmented matrix we've
been working with.
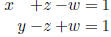
Recall that the system has the following solution set:
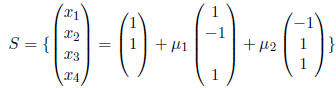
Then
says that 
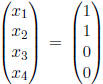solves
the system , which is
certainly true.
says that
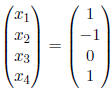solves the system.
says that 
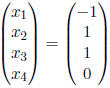solves
the system.
Definition Let M a matrix and V a vector. Given the linear system MX =
V , we call
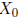a particular solution if
. We call Y a homogeneous
solution if MY = 0.
The linear system MX = 0 is called the (associated) homogeneous sys-
tem.
If is a particular solution, then the general solution to the system is:
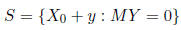
In other words, the general solution = particular + homogeneous.
Review Questions
1. Write down examples of augmented matrices corresponding to each
of the five types of solution sets for systems of equations with three
unknowns.
2. Let
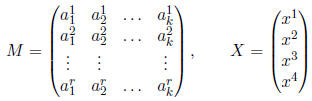
Propose a rule for MX so that MX = 0 is equivalent to the
linear
system:
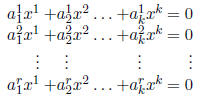
Does your rule for multiplying a matrix times a vecotr
obey the lin-
earity property ? Prove it!
3. The standard basis vector ei is a column vector with a
one in the
ith row, and zeroes everywhere else. Using the rule for multiplying
a matrix times a vector in the last problem, find a simple rule for
multiplying Mei, where M is the general matrix defined in the last
problem.
| Prev | Next |