The Twenty-One Commandments
Some helpful guidelines. Stick to this path and you'll do
well in math.
1. Never divide by zero.
2. Be careful about taking the square root of a negative number.
3. When you take the square root of both sides of an equation, you get a " ± ".
4. Beware of witchcraft cancelations.
5. When you substitute , use parentheses.
6. Beware of the (incorrect) belief that everything distributes.
7. Don't set something equal to zero unless there's a good reason why it should
actually be equal to zero.
8. Use the symbol "=" appropriately.
9. Identify the types of objects you're working with.
10. Know the Quadratic Formula (correctly).
11. Never write down a new symbol without explaining what it represents.
12. If some symbol has a specific value, then don't call it by the old name
anymore.
13. Use parentheses appropriately .
14. Explain yourself.
15. Avoid pronouns.
16. Know and understand the "Zero Product Property."
17. Check your work.
18. Avoid the Guess-and- Check method .
19. Don't treat equations like numbers .
20. If a question asks you to show that a certain claim is always true, don't
just show
that it's sometimes true.
21. Take baby steps .
The details on what I mean:
1. Never divide by zero.
In fact, whenever you do any division, you must ask yourself, when can the thing
I'm
dividing by equal zero? (This is especially important to remember when you're
doing
a "cancelation" that is really division.) This problem is easy to spot when it's
written
out directly, like if you see "3/0". What you have to be careful of are the less
obvious
situations like 3/(x+4). Here, depending on what x is, the denominator might by
zero.
2. Be careful about taking the square root of a negative number.
With this one, it depends what you're doing. Square roots of negative numbers
are
"imaginary" or "complex" numbers, which are perfectly good, genuine numbers,
they're
just not what we call "real" numbers. In some situations, we do use them. But
when
we're talking about the domain or range of a function, or anything related to
graphs ,
for instance, we traditionally only work with real numbers, and so taking the
square
root of a negative number becomes illegal.
Three additional remarks : (1) The square root of zero is real:
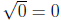 .
.
(2) The above is not talking about the square roots themselves being negative;
it's
talking about the number you plug into the square root being negative.
(3) All statements in this commandment and the next one also apply to fourth
roots,
sixth roots, eighth roots, etc.-all even-index roots.
3. When you take the square root of both sides of an equation, you get a "±
".
The term "square root of c" means any number whose square is c, that is, any
solution
x to the equation x2 = c. Of course, if c < 0, there are no solutions
(see above), and if
c = 0, there is only one solution (x = 0).
But if c > 0, then there are two different solutions to x2 = c, i.e. two
different square
roots of c. The symbol " 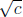 " is our shorthand for the positive solution ; sometimes we'll
" is our shorthand for the positive solution ; sometimes we'll
refer to 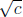 as "the" square root of c, but that's a little misleading, because there's
as "the" square root of c, but that's a little misleading, because there's
another: -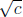 . So the solutions to x2 = c are x =
. So the solutions to x2 = c are x =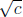 and x = -
and x = -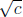 ; we shorthand
; we shorthand
this by writing x = ± 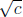 , but never forget that the " ± " is not a single symbol, but a
, but never forget that the " ± " is not a single symbol, but a
shorthand for two different things .
So the punchline is, if you've got some equation left =right, and you want to
take
the square root of both sides, you need to write
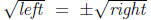 (in other words,
(in other words,
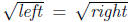 or
or 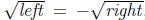 , so there's sort of a fork in the road-there are
, so there's sort of a fork in the road-there are
two equations now). If you forget the ±, you're literally missing 50% of the
possibilities.
Does it matter which side of the equation you put the ± on? No. Should you put a
±
on both sides? No; it wouldn't really be incorrect if you did, but it is
confusing and
unnecessary, as the second ± turns out to be redundant.
4. Beware of witchcraft cancelations.
For instance, tons of people would do the following (or something logically
equivalent ):
| false false false |
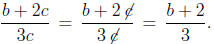 |
false false false |
This is untrue. Why? Well what's the germ of the correct
idea here? It's that 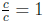 ,
,
so 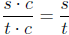 . In other words, if you can factor c out of the numerator and denominator
. In other words, if you can factor c out of the numerator and denominator
of a fraction, then the c's "cancel" away.
But this only works if that's what you're actually doing-i.e., you need to
factor c out
of the entire numerator and the entire denominator of the fraction. In the
example
above, this is not done. if you were to factor c out of the numerator, you would
get that
b + 2c = (b/c + 2) · c. So it is true that
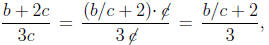
although it's debatable whether this is progress or not.
There are other kinds of "witchcraft cancelations," but the above type is the
most
common . Just beware of wishful thinking. Avoid the logic that says, "oh, here's
a c,
and here's another-let's cross them both out." If you can't explain your
wished-for
cancelation in terms of basic algebra facts, don't do it.
5. When you substitute, use parentheses.
In any situation where you are replacing a variable with an expression, surround
that
expression with parentheses when you put it in. For example:
If 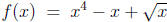 , then
, then
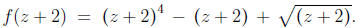
As you can see, I replaced every x in the first equation with a (z+2)-not just
z+2-in
the second. I like to think of the parentheses around the z + 2 as a kind of
packaging,
like a box or envelope, that keep the z and the 2 from getting separated in
transit.
Generally speaking, these parentheses are not optional. For instance, (z+2)4
and z+24
are not the same thing. Even if you mentally treat the second expression as if
it had
parentheses, that's not good enough-you need to say what you mean.
Occasionally, the parentheses won't actually do anything; for instance,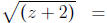 ..
..
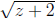 In situations like that, you should get rid of the parentheses as soon as
you
In situations like that, you should get rid of the parentheses as soon as
you
notice that they don't serve a purpose. And if you can tell ahead of time that
they
won't do anything, you can leave them out. But in my opinion, until you're
experienced
enough to be consistently right, better safe than sorry.
6. Beware of the (incorrect) belief that everything
distributes.
We know that c · (a + b) = c · a + c · b; in other words, if you apply the
"multiplication
by c" process to the sum a+b, it's the same as applying it to a and b
individually. This
is a consequence of the Distributive Property of multiplication .
The Distributive Property is a very special property of multiplication. For
other math-
ematical processes, like square-rooting or exponentiating, there are similarly
flavored,
believable-looking claims that a person could make; many of the important facts
of alge-
bra that you know are of this form. For instance, it's true that (a · b)2
= a2 · b2,
i.e. if you
multiply two numbers, then square the result, it's the same as first squaring each
num-
ber then multiplying-we say that "squaring distributes across multiplication."
Similar
things are true if you replace squaring with cube-rooting or taking absolute
values.
But here's the kicker-most statements that have this kind of flavor are untrue.
The rule of thumb is, if we don't tell you that it's true, it probably isn't.
Below is a
sampling of the most "popular" incorrect beliefs of this type.
| false | false false false false false false false false false false | false |
| false | 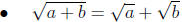 (in particular, (in particular,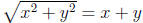 .) .) |
false |
| false | 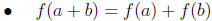 for every
function f(x) for every
function f(x) |
false |
| false | 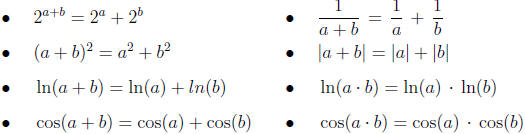 |
false |
| false | false | |
| false | false | |
| false | false | |
| false | etc. etc. etc. | false |
| false | false false false false false false false false false false | false |
| Prev | Next |