Algebraic Review
Most of this material is review from CS 173, though
students may have forgotten some
of it, especially details of notation. The exceptions are the sections on
strings and graph
induction.
Before you start, introduce yourself. Promise office hours will be posted very
soon and
encourage them to come.
1 Homework guidelines
• Put each problem on a different sheet of paper, we grade them separately.
• Put your name on each sheet of paper you submit.
• Put the section number on every sheet of paper you submit.
• Homeworks will usually be due Mondays at 4pm.
• The next homework is due next Tuesday.
Do not forget to register with the news server and start reading the news-
groups !
2 Numbers
What are Z, N (no zero), N0, (mention quickly Q and IR).
3 Divisibility
What does it mean for x to divide q ? Namely, there exists integer n such that q
= xn. As
such, every number n is divisible by 1 and n (i.e., itself).
An integer number is even if it can be divided by 2. A number which is not even,
is odd.
Q: Is zero even ? Well, 0 = 2· 0 and as such, 0 is divisible by two.
Meaning of p = q mod k. Examples... (i.e., 121 = 73 mod 3).
4
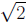is not rational
A number x is rational if it can be written as the ratio of two integers
.
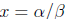The fraction
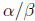is irreducible if α and β do not have any common divisors (except 1, of course).
Note
that a rational number has a unique way to be written in irreducible.
Lemma 4.1 An integer k is even if and only if k2 is even.
Proof: If k is even, then it can be written as k = 2u, where u is an integer. As
such,
k2 = (2u)2 = 4u2is even, since it can be divided by 2. As for the other
possibility, if
k = 2u + 1, then
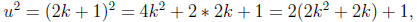
is odd (since it is the sum of an even number and an odd number), implying the
claim.
Theorem 4.2 The number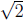 
is not rational (i.e.,
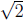is an irrational number).
Proof: Assume for the sake of contradiction that
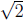is rational, and it can
written as the
irreducible ratio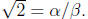 
Let us square both size of this equation. We get that
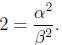
That is the number 2 is a divisor of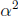 
. Namely,
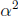is an even number. But then,
α must
be an even number. So, let α= 2a. We have that
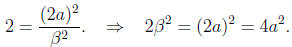
As such,
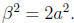
Namely,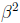 
is even, which implies, again that
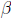is even. As such, let us write
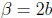, where
b is an integer. We thus have that
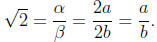
Namely, we started from a rational number in irreducible form (i.e.,
) and we
reduced
it further to a/b. But this is impossible. A contradiction. Our assumption that
is a
rational number is false. We conclude that
is irrational.
5 Review of set theory
Sets, set building notation (just show an example), subset, proper subset, empty
set, Venn
diagram
Tuples, cross product of two sets .
Sets of sets, power set , sets can contain a mixture of stuff like
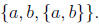
Demorgan' s Laws
Cardinality of a set
6 Strings
strings, empty string, sets of strings
substring, prefix , suffix, string concatenation
What happens when you concatenate the empty string with another string?
Suppose w is a string. Is the empty string a substring of w? (Yes!)
7 Recursive definition
Recursive definition (concrete example).
Let U be the set that contains the point (0, 0). Also:
•
if (x, y)∈ U, then (x + 1, y) ∈ U.
•
if (x, y) ∈ U, then (x, y + 1) ∈ U
Q: What is U?
A: Clearly, (0, 1)∈ U, (0, 2) ∈ U,.... (0, k) ∈ U (for any k).
As such, (1, k) ∈ U (for any k)
As such, (2, k)∈ U (for any k)
As such, (j, k) ∈ U (for any j > 0, k > 0).
Note that
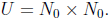
(A more complicated example of this is in the homework.)
8 Induction example
The following wasn't done in some (all?) of the sections, but you may still find
it useful to
read.
Consider a graph G = (V,E). The graph G is connected, if there is a path between
any
two vertices of G. A graph is acyclic if does not contain any cycle in it. A
leaf in G is a
node that has exactly one edge adjacent to it.
Lemma 8.1 A connected acyclic graph G over n > 1 vertices, must contain a leaf.
Proof: Indeed, start from a vertex v ∈ V (G), if it is a
leaf we are done, otherwise, there
must be an edge e = vu of G adjacent to v (since G is connected), and travel on
this edge
to u. Mark the edge e as used. Repeat this process of \walking" in the graph
till you reach
a leaf (and then you stop), where the walk can not use an edge that was used
before.
If this walk process reached a leaf then we are done. The other possibility is
that the
walk never ends. But then, we must visit some vertex we already visited a second
time (since
the graph is finite). But that would imply that G contains a cycle. But that is
impossible,
since G is acyclic (i.e., it does not contain cycles).
Claim 8.2 A connected acyclic graph G over n vertices has exactly n - 1 edges.
Proof: The proof is by induction on n.
The base of the induction is n = 2. Here we have two vertices, and since its
connected,
this graph must have the edge connecting the two vertices, implying the claim.
As for n > 2, we know by the above lemma that G contains a leaf, and let w
denote this
leaf.
Consider the graph H formed by G by removing from it the vertex w and the single
edge
e' attached to it. Clearly the graph H is connected and acyclic, and it has n -
1 vertices.
By the induction hypothesis, the graph H has n - 2 edges. But then, the graph G
has all
the edges of H plus one (i.e., e'). Namely, G has (n - 2) + 1 = n - 1 edges,
as claimed.
| Prev | Next |