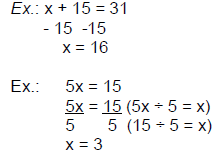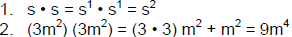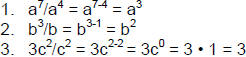Compass Math Sample

Find the Unknown:

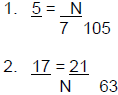
3. Nicole is a beautician. She takes care of 9 customers in 5 hours. What is the ratio of
customers to hours?

4. Jan earns $2.00 in commissions for every $5.00 in business. If she brings in
$325.00, how much money will she get in commissions?

5. A town wants to keep its ration of 7 parks to 5,000 people. If the town grows to
15,000 people, how many parks will it need?

6. If a plane flew 932 miles in 2 hours, how far will it fly in 7 hours?

Solving Equations

• Get the unknown on one side of the = sign and its value on the other side of the sign
• Use the opposite operation (-,+,x,÷) of the one shown in the equation
• Any operation (-,+,x,÷) performed on one side of the equation must be performed on
the other side of the equation
• The opposite of – is +, and the opposite of x is ÷

5. A light blue paint is made by mixing 2 parts of blue paint to 7 parts of white paint.
Using a proportion, determine how many pints of blue paint (N) should be mixed with
28 pints of white paint to make this light blue color.

6. Northwest reduced its roundtrip
ticket from Boston to Washington by $62. The sale
price was $169.95. What was the original price?

7. Amy and Kay sold a total of 560 cosmetic kits. Amy sold 6 times as many kits as
Kay. How many did each sell?

Key Words in Word Problems:
• Addition: Total, Sum, Increase, Together, Both, Altogether, Whole
• Subtraction: Difference, Remainder, How much less, How much more, How much is
left, Decreased by
• Multiplication: Product, Times, Of, Apiece
• Division: Quotient, Average, Shared, Equally, How many times

Signed Numbers
Adding Signed Numbers:
• Add all the positive numbers, make the total positive
• Add all the negative numbers , make the total negative
• Compare the two totals by subtracting the smaller from the larger, and give the
answer the sign of the larger total

Ex.: Add

1. (+3)+(-5)+(+12)+(-9) Positive total: + 3 + 12 = +15 Negative total: -5– 9 = -14 Comparison: +15 –14 = +1 ( or simply 1)	2. (-9)+(+10)+(-8)+(+4) Positive Total: (+10) + (+4) = +14 Negative Total: (-9)+ (-8)= -17 Comparison: +14 –17 = -3

1. (+5) + (-8)+ (+9) = 2. -18+ (-2)+6 = 3. 6 + (-8)=	4. (-9)+ (-4)+ (8) + (7) + (-2)= 5. Find the sum of : +8, -6,-5 6. Simply: -10+ (-13)+ (-26)

Subtracting Signed Numbers:
• Change the sign of the number being subtracted to the opposite sign
• Follow the rules for adding signed numbers

Ex.: Subtract

Multiplying Signed Numbers:
• When multiplying 2 numbers together, if the signs of the numbers are alike, the
answer is positive
• If the signs of the numbers are different, the answer is negative

Ex.: Multiply

a. (-8)(-7)= 56	b. -3 · 10 = -30
Since the signs are alike, the answer is positive.	The dot between the numbers is a symbol for multiplication. Since the signs are different, the answer is negative.
c. (-6)(+2) (-3)(+4)	d. (-2)(-11)(+3) (-5)
An even number of – signs gives a positive number.	An odd number of – signs gives a negative number.

Dividing Signed Numbers:
• If the signs of the numbers being divided are alike, the answer is positive
• If the signs of the numbers being divided are different, the answer is negative
Ex.: Divide

30 / -6= -5	-28/-12= +2 1/3
Since the signs are different, the answer is negative.	Remember the fraction bar implies division. Since the signs are alike, the answer is positive.

EXPONENETS AND MONOMIALS

Exponents:
• The formula for finding a volume of a prism is v = lwh. A cube is a prism that has
equal dimensions. Let s represent the length of each edge. So, the formula for the
volume of a cube is v = s x s x s or v = s³ (pronounced s cubed). The 3 in the
expression s³ is called the exponent. The s is called the base. The exponent
indicates the number of times the base is listed as a factor.

• When no exponent is used, as in A = lw, the exponent of each variable is understood
to be 1. If an expression contains factors that are repeated , you can rewrite the
expression using exponents.

• Remember y x y, y · y, and (y) (y) all mean multiply

5. A cube has edges 5 inches long. What is its volume?

6. Write r · r · r using an exponent.

Multiplying Monomials:
• When like bases are multiplied, the exponents are added. When monomials have
coefficients other than 1, remember to multiply coefficients.
Ex: Multiply

Dividing Monomials:
• Division is the reverse of multiplication. When monomials are multiplied, exponents
of like bases are added. When monomials are divided, exponents of like bases are
subtracted. When monomials have coefficients other than 1, remember to divide the
coefficients.

• Recall that expression such as 5/5 and a/a equal 1. If you use the rule for dividing
monomials, you see that a/a = a; therefore, any base raised to the zero power equals
one.

Ex: Divide