Elementary Algebra
• COURSE NAME: Elementary Algebra
• INSTRUCTOR: Dr. Kamal P. Hennayake
• OFFICE: S - 122
• OFFICE HOURS: Monday, Tuesday, Wednesday, and Thursday: 11:30 am –
12:45 pm
• PREREQUISITE: MAT 023 or appropriate score on the placement test.
• COURSE DESCRIPTION: “An introduction to algebra. Topics include
properties of whole
numbers, integers and rational umbers; solving equations; polynomials;
factoring; systems of
equations and graphs. ”
• (Three hours per week), three load hours, 0 credits.
• Now that you have decided to take this course, remember that a positive
attitude will make all
the difference in the world . Your belief that you can succeed is just as
important as your
commitment to this course. Make sure that you are ready for this course by
having the time and
positive attitude that it takes to succeed.
• In this course you will study:
o Solving Equations and Inequalities
o Graphing Equations and Inequalities
o Exponents and Polynomials
o Solving Systems of Equations
o Problem Solving
• This course is intended to provide a useful background in mathematics for
students pursuing any
degree or certificate. This is the middle step in your non -credit mathematics.
This is
approximately equivalent to the first year of high school algebra. In this
course, you will learn
many new concepts and see the expansion of several familiar ones. All the topics
in this course
are designed to prepare you for subsequent courses in Mathematics. You will be
doing some
applications that will help you understand the relevance of what you are
learning. As your
mathematical expertise expands in succeeding courses, the applications of your
skill will become
even more diverse and interesting. Your ability to succeed in those later
courses will very much
depend on how well you understand the material covered in this course.
• Scientific or graphing calculators may also be used to further illustrate
specific concepts.
• In addition to the class time, the average student should plan to spend six
hours outside of
class each week (2 hours for every hour spent in class). Students whose
background in
mathematics is below average, or who normally work at a slower than average
pace, should
schedule more time in order to keep up with the course material.
• REQUIRED COURSE MATERIALS:
o TEXTBOOK: Foundations of Mathematics by Marvin L. Bittinger and Judith
A. Penna.
Addison Wesley. 2004 ISBN # 0-321-16856-9
o CALCULATOR
o Pencil and a notebook to keep a very good set of notes. A separate
notebook to do the
homework.
• COURSE REQUIREMENTS:
o 11 pop quizzes (20 points each, best ten will be counted for total of 200
points)
o 5 tests (100 points each, best four will be counted for total of 400 points)
o 1 comprehensive final examination (100 points)
• Tests: At the end of each module you’ll take a test. Each test is worth
100 points. You are
not allowed to use notes or textbooks for your tests. Don’t forget to bring a
pencil, and a
calculator. If you missed a test for any reason, you have a zero for that test .
There are no
makeup test unless for an emergency.
• Final exam is a comprehensive exam. Everyone must take it in class.
• Quizzes: There will be pop quizzes at the beginning or at the end of
class. There are no
makeup quizzes.
• In order to comfortably succeed in MAT 031 you will need to be proficient in
the following
skills. If you need to brush up on any of these skills please ask for help
immediately!
o Basic number sense
o Add, subtract, multiply and divide integers and fractions
o Use of exponents and the order of operations
o Arithmetic operations of sign numbers
• Attendance: Research shows that attendance is the single most important
factor in school
success. Most students need guidance in understanding the procedures
involved in developing a
new mathematical process. If you find yourself unable to keep up with the class,
make an
appointment immediately to see the instructor outside of class time. Learning
builds day by day.
If you miss a day of class, you miss a day of learning. It is the student's
responsibility to
make up any work missed due to an absence for any reason.
• Academic Honesty: As a reminder, the College has a policy on academic
honesty. You are
expected to abide by the procedures set forth in the document.
• Accommodating Disabilities: Any student in this course who has a disability
that may prevent
him or her from fully demonstrating his or her abilities should contact the
instructor as soon as
possible, so we can discuss accommodation necessary to ensure full participation
and facilitate
your educational opportunity.
• College policy prohibits young children from
accompanying parents to class.
• Classroom Etiquette: It is assumed that all students will respect each
other’s rights to fully
participate in the discussion of the day. To that end, it is expected that
students will not engage
in behaviors that distract not only the instructor but also their fellow
classmates. Students who
engage in activities such as talking to each others, talking on cell phones or
text messaging,
leaving class for non-emergency needs, will be asked to leave. If you are
unlucky enough to be
one of these students, you will be required to meet with me in my office prior
to returning to
class. I expect that all of my students will behave in an adult, respectful and
professional
manner. Students are prohibited from using, activating or displaying personal
electronic devises.
• GRADES: The numerical final course grade will be computed as indicated
in the following
distribution , and letter grades will be assigned as follows.
| Components of Final Grade | Letter grade | Points | |
| Quizzes | 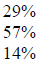 |
 |
90% or more |
| Tests | 80% - 89% | ||
| Final Examination | 70% - 79% | ||
| Less than 70% | |||
• TESTING: Dates for tests are given on the
syllabus. You should make a special effort to be
present for class on those days, but should it be absolutely necessary to
miss a scheduled
test, the student should contact the instructor as early as possible to make
other arrangements
for testing. A separate make-up test will be given only for an extreme
emergency, and
will be scheduled at the instructor's convenience.
If you are absent prior to a scheduled test, you will still be expected to take
the test at the
scheduled time and are expected to contact a classmate or the instructor in
advance to
obtain the information required to prepare for the test.
Although you will be tested on the subject matter of each chapter, tests for
specific sections may
be combined so as to maximize course effectiveness. The following outline may be
modified
slightly as necessary to accommodate student needs and to permit possible
computer and/or
video demonstrations. A brief description of the Objectives for each
chapter is detailed on the
following pages.
This course consists of all or parts of chapters #7, #8, #19, #12, #13 and #14
in the assigned
textbook. The following syllabus outlines in detail the material, which will be
presented from
each of the chapters, and the intended order of presentation.
COURSE OUTLINE
| CHAPTER | TOPIC COVERED |
| Seven | Solving Equations and Inequalities |
| Eight | Graphs of Linear Equations |
| Nine | Polynomials: Operations |
| Twelve | Graphs, Functions and Applications |
| Thirteen | Systems of Equations |
| Fourteen | More on Inequalities (Optional) |
CHAPTER OBJECTIVES
After completing each chapter the student should be able to accomplish the
following:
Chapter Seven – Solving Equations and Inequalities
OBJECTIVES:
1. Solving equations using the addition principle.
2. Solving equations using the multiplication principle.
3. Solve equations using both the addition and multiplication principle.
4. Solving a formula for a specific letter.
5. Solve applied problems involving percent.
6. Solve applied problems by translating to equations.
7. Solve inequalities using the addition and multiplication principles together.
8. Solve applied problems using inequalities.
Chapter Eight – Graphs of Linear Equations
OBJECTIVES:
1. Solve applied problems involving circle, bar, and line graphs.
2. Solve applied problems involving graphs of linear equations.
3. Find the intercepts of a linear equation, and graph using intercepts.
4. Find the slope of a line.
5. Apply steps for problem solving.
6. Use formulas to solve problems.
7. Solve application problems involving percents.
8. Solve and graph the solution set for a linear inequality in one variable.
Chapter Nine – Polynomials: Operations
OBJECTIVES:
1. Evaluate expressions with integer exponents.
2. Use product , power and quotient rules to evaluate exponential expressions.
3. Evaluate expressions raised to a negative integer exponent.
4. Solve applied problems using scientific notation.
5. Identify types of polynomials.
6. Add, subtract, multiply and divide polynomials.
7. Use synthetic division to divide a polynomial by a binomial .
Chapter Twelve – Graphs, Functions, and Applications
OBJECTIVES:
1. Solve applied problems involving functions and their graphs.
2. Find the domain and the range of a function.
3. Solve applied problems involving slope.
4. Graph linear equations.
5. Solve applied problems involving linear functions.
Chapter Thirteen – Systems of Equations
OBJECTIVES:
1. Solve a system of two linear equations or two functions by graphing.
2. Solve systems of two equations in two variables by substitution method.
3. Solve systems of two equations in two variables by the elimination method.
4. Solve applied problems using systems of two equations.
Chapter Fourteen – More on Inequalities
OBJECTIVES:
1. Write interval notation for the solution set of an inequality.
2. Solve an inequality using the addition and multiplication properties.
3. Find the intersection and union of two sets, and then graph the inequalities.
4. Find the distance between two points.
5. Solve equations containing absolute value expressions .
6. Solve inequalities containing absolute value expressions.
7. Graph linear inequalities in two variables.
8. Graph systems of linear inequalities in two variables and find the
coordinates of any
vertices.
Learning Outcomes
Students will be able to:
1. Perform calculations with integers.
2. Solve applied problems by writing the appropriate equation and solving it
appropriately.
3. Add, subtract. Multiply and divide polynomials.
4. Perform operations with exponents.
5. Use equations and inequalities to solve problems.
6. Evaluate exponents written in function notation.
REVIEW SHEET FOR THE FINAL EXAMINATION
The final examination for this course consists of fifty computational questions.
The
problems are similar to those that you have worked to complete each unit and
similar to the
questions you experienced on each quiz. One way to review all the material from
this course is to
work the Chapter Review located at the end of each chapter. Further, you may
find it beneficial to
review the Chapter Highlights at the end of each chapter. There you will find an
example of each of
the concepts. If you have any difficulties you should review that section of the
chapter more
thoroughly. If you have any questions, be sure to ask before you take the final
examination.
A suggested list of topics that you should review includes, but is not
necessarily limited to:
1. Add, subtract, multiply and divide signed numbers.
2. Write and simplify expressions using exponents.
3. Combine like terms in a given expression.
4. Solve equations, inequalities and literal equations .
5. Given two points, find the slope of the line containing them.
6. Evaluate expressions containing positive and/or negative exponents.
7. Multiply monomials, binomials and trinomials.
8. Divide monomials and divide by binomials.
9. Given sufficient information write the equation of a straight line.
10. Given two points find the slope of the line containing them.
11. Solve all type of application problems.
| Prev | Next |