Finding the Greatest Common Factor

Definition: The Greatest Common Factor (GCF) is the largest number/expression that `
divides into two or more expressions evenly .

For Example: For the numbers 18 and 27, 3 is a common factor, but 9 is the greatest
common factor , since 9 is the largest number that divides into 18 and 27
evenly.

Finding the GCF: One approach to finding the GCF is looking at the prime factors that
occurs the least (look for the smallest exponent ) in each of the numbers or expressions
that are involved. For instance, in the previous example , 18 and 27, factor each number
into its prime factors.

The least exponent on the 3 is two and on the 2 is zero (since 27 does not have any
factors of 2) so the GCF is 3² = 9.

Another example of finding the GCF of 90 and 120:

The least exponent of each factor is one so the GCF is 2●3●5 = 30.

Examples for Finding the GCF of Algebraic Expressions :

The same approach is used to find the GCF of algebraic expressions — factor into prime
factors first .

Example: Find the GCF of 12x²y³w and 20xy².

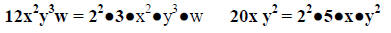
Choose the least exponent for each factor. So the GCF is 2²●x●y² (3, 5 or w did not occur
in both expressions so they are not part of the GCF).

Example: Find the GCF of 3x³ + 6x² and 6x² – 24

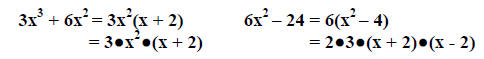
The GCF is 3(x + 2)