Fractions
A fraction is just a shorthand way of expressing a division problem. In other words, 5/2 = 5÷2. The Numerator is the ‘top’ number in a fraction and the Denominator is the ‘bottom’ number. For example: 5/2, the 5 is the numerator and the 2 is the denominator.
When adding and subtracting fractions , the denominators of the fractions must be the same. If the denominators of the fractions are already alike, just add or subtract the numerators and put the result over the common denominator. For example,
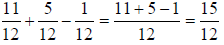
If the denominators of the fractions are different , multiply the fraction(s) by the fractional form(s) of the number 1 which makes the denominators the same. For example,
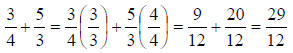
Since 12 is the lowest common denominator of 3 and 4, then we had to multiply by 3/3 and 4/4 to get 12 in both denominators. Since 3/3 and 4/4 both equal 1, we are not changing the value of the fractions . 1 is the only number you can multiply by without changing the values of the fractions.
When multiplying fractions, simply multiply the numerators
and multiply the denominators; then reduce. Reducing fractions is discussed
below. For example,
(5/7)*(2/3) = 10/21. When one fraction is multiplied by another fraction, the
product is smaller than either of the original fractions.
When dividing fractions, invert (put the denominator over
the numerator) the second fraction and multiply. For example, (5/7)÷(1/3) =
(5/7)*(3/1) = (5*3) /(7*1) = 15/7.
The GRE may include problems in which the numerator or denominator itself is a
fraction such as 5/(2/3). Just remember this is just another notation for
division. For example, 5÷(2/3) = 5*(3/2) = (5/1)*(3/2) = 15/2.
When adding, subtracting, multiplying, and dividing fractions, you must make sure the final fraction is in reduced form, especially if your final answer does not appear in the answer choices. Consider the example we used when discussing adding and subtracting fractions. The answer we got was 15/12. This answer would probably not appear as one of the answer choices for that question on the GRE because this fraction is not reduced. To reduce a fraction, simply factor the numerator and denominator into prime factors and cancel out like factors :
15/12 = (3*5)/ 2*2*3) = 5/(2 * 2) = 5/4
Another way to tackle this problem is to just divide the numerator and the denominator by the largest factor that is common to both which in this example would be 3. The result would be 5/4.
A mixed number is a fractional number greater than 1 which
is expressed as a whole number and a fraction such as
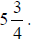In most cases on the GRE, you will need to
convert mixed numbers to fractions by multiplying the denominator by the whole
number, adding this product to the numerator, and putting this sum above the
denominator. For example,
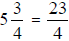
To convert a fraction greater than 1 to a mixed number,
divide the denominator into the numerator to get the whole number and put the
remainder over the denominator to get the fractional part. For example,
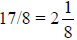
The GRE may ask you to compare fractions and decide which one is larger or smaller. There are two ways to compare fractions. One way is to find a common denominator and multiply the fractions by the fractional forms of 1 that give them the same denominator. For example, suppose we want to know which fraction is larger, 3/7 or 7/14. Since 14 is a common denominator, multiply 3/7 by 2/2 to get 6/14. Clearly 7/14 is larger than 6/14.
Another method for comparing fractions is cross-multiplication. Consider the two fractions in the example above, 3/7 and 7/14. In cross-multiplication, multiply the denominator of each fraction by the numerator of the opposite fraction; then compare the two products as follows.
14*3 is 42 and 7*7 is 42. Since 49 is bigger than 42, 7/14 is bigger than 3/7. When cross-multiplying you must be careful to work from bottom to top in the direction of the arrows. Had you multiplied numerator by denominator working from top to bottom, you would have gotten the wrong answer.
The following is an example of a GRE question asking you to compare more than two fractions. Example: Which of the following fractions is smaller?
4/7
5/8
8/11
To solve this type of problem, just compare the fractions two at a time. First, compare 4/7 and 5/8 and eliminate the largest of the two. The smallest of these two is 4/7. Now compare 4/7 to 8/11 and eliminate the largest. The smallest fraction is 4/7.
One reminder about fractions: if the denominators are
alike and the numerators are different, the one with the largest numerator is
the largest fraction; if the numerators are alike and the denominators are
different, the one with the largest denominator is the
smallest fraction. For example, 11/13 is larger than 11/14. If both the
numerators and the denominators are different, you must use one of the methods
described above to determine which is larger.
EXERCISE 2
1. Reduce each of the following fractions:
(a) 5/20 (c) 51/39 (e) 78/48
(b) 18/24 (d) 45/56 (f) 12/63
2. Perform the following operations :
(a) 5/6 + 9/10 (c) 6/25 ÷ 15/2 (e) 15/32 – 7/8
(b) (2/3)/6 (d) 5 + 5/6 (f) (3/10)/(2/15)
3. Determine the larger fraction in each pair of the following fractions:
(a) 28/53, 27/53 (b) 14/21, 14/22 (c) 7/5, 11/12
4. Convert the mixed number
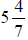to a fraction.
5. Convert the fraction 25/7 to a mixed number.
6. How many halves are in the number 6? How many thirds?
| Prev | Next |