Mathematics Meet
Problem 1
Michael is celebrating his fifteenth birthday today. How
many Sundays have there been in his
lifetime?
Problem 2
Evaluate
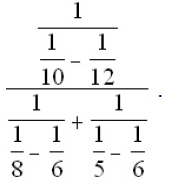
Problem 3
Find the sum of all the prime numbers less than 100 which are one more than a multiple of six.
Problem 4
At the beginning of each hour from 1 o’clock AM to 12 NOON
and from 1 o’clock PM to 12
MIDNIGHT a coo-coo clock’s coo-coo bird coo-coos the number of times equal to
the number
of the hour. In addition , the coo-coo clock’s coo-coo bird coo-coos a single
time at 30 minutes
past each hour. How many times does the coo-coo bird coo-coo from 12:42 PM on
Monday until
3:42 AM on Wednesday?
Problem 5
The sizes of the freshmen class and the sophomore class
are in the ratio 5:4. The sizes of the
sophomore class and the junior class are in the ratio 7:8. The sizes of the
junior class and the
senior class are in the ratio 9:7. If these four classes together have a total
of 2158 students, how
many of the students are freshmen?
Problem 6
We draw a radius of a circle . We draw a second radius 23
degrees clockwise from the first
radius. We draw a third radius 23 degrees clockwise from the second. This
continues until we
have drawn 40 radii each 23 degrees clockwise from the one before it. What is
the measure in
degrees of the smallest angle between any two of these 40 radii?
Problem 7
At a movie theater tickets for adults cost 4 dollars more
than tickets for children. One afternoon
the theater sold 100 more child tickets than adult tickets for a total sales
amount of 1475 dollars.
How much money would the theater have taken in if the same tickets were sold,
but the costs of
the child tickets and adult tickets were reversed?
Problem 8
A rogue spaceship escapes. 54 minutes later the police
leave in a spaceship in hot pursuit. If the
police spaceship travels 12% faster than the rogue spaceship along the same
route, how many
minutes will it take for the police to catch up with the rogues?
Problem 9
Moving horizontally and vertically from point to point
along the lines in the diagram below, how
many routes are there from point A to point B which consist of six horizontal
moves and six
vertical moves?

Problem 10
How many rectangles are there in the diagram below such
that the sum of the numbers within the
rectangle is a multiple of 7?
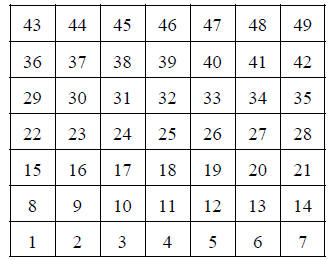
Problem 11

Find the coefficient of 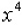 in
in 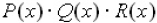 .
.
Problem 12
How many positive integers divide the number 10! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 ?
Problem 13
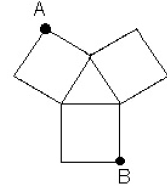
An equilateral triangle with side length 6 has a square of
side length 6
attached to each of its edges as shown. The distance between the two
farthest vertices of this figure (marked A and B in the figure) can be
written as 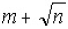 where m and n are positive
integers .
where m and n are positive
integers .
Find m + n.
Problem 14
The rodent control task force went into the woods one day
and caught 200 rabbits and 18
squirrels. The next day they went into the woods and caught 3 fewer rabbits and
two more
squirrels than the day before. Each day they went into the woods and caught 3
fewer rabbits and
two more squirrels than the day before. This continued through the day when they
caught more
squirrels than rabbits. Up through that day how many rabbits did they catch in
all?
Problem 15
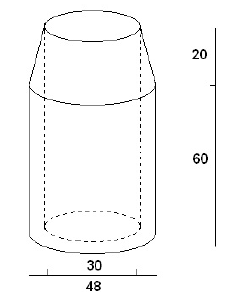
A concrete sewer pipe fitting is shaped like a cylinder
with diameter 48 with a cone on top. A
cylindrical hole of diameter 30 is bored all the way through the center of the
fitting as shown.
The cylindrical portion has height 60 while the conical top portion has height
20. Find N such
that the volume of the concrete is Nπ.
| Prev | Next |