Decimal Fraction
1. Decimal Fractions .
(a) Prove that every rational number has either a terminating or repeating expansion. (Hint. long division.)
(b) In light of the last question, give me a clear way to
generate an
infinite decimal expansion that does not repeat, thus constructing
an irrational number . Be sure I can tell how to generate each digit
and also make an argument why it does not repeat.
(c) Consider an infinite decimal expansion
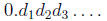Write it as
a limit of a sequence of truncated ("cut-off") decimal representations .
(d) Prove that the sequence in the last question is
Cauchy. (Reminder.
a sequence an is Cauchy if for any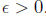 
, there is
a natural number
N such that if m, n > N, then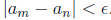 
)
(e) (don't turn in) Remind yourself what a completion of a
metric
space is, and convince yourself that the real numbers are the completion of the rational numbers .
(f) Write 0.999 . . . as the limit of a sequence of
terminating decimals .
Prove that the limit of this sequence is 1. Yes, you'll have to use
an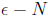 
argument.
2. Comparing Set Cardinalities. Prove using the
definition of "same
size" and "fits in" in class that the following pairs of sets have the same
size.
(a) Prime numbers and whole numbers.
(b) Terminating decimals and repeating decimals (here you can count
an infinitely repeating 0 as repeating).
| Prev | Next |