Basic Algebra: Unit 8 Factoring Part II
Special Cases of Factoring
Difference of Two Squares
a2 − b2 = (a − b)(a + b).
Perfect Square (two cases)
a2 + 2ab + b2 = (a + b)2,
a2 − 2ab + b2 = (a − b)2.
Sum and Difference of Cubes
a3 + b3 = (a + b)(a2 − ab
+ b2),
a3 − b3 = (a − b)(a2 + ab + b2).
These should be used as formulas you have memorized, not
something you “work out”. You can “work out” the difference
of square and perfect square cases using the grouping method of factoring if you
have to , but the sum and difference of
cubes must be used as memorized formulas.
Example Factor 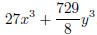
Notice that this looks like it might be a sum of cubes. Try to write in terms of quantities cubed:
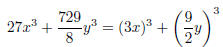
Now, use the appropriate formula you have memorized: a3
+ b3 = (a + b)(a2 − ab + b2). Identify: a = 3x, 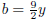 .
.
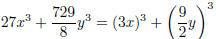
= (a)3 + (b)3 identify is as sum of cubes
= (a + b)(a2 − ab + b2) use sum of cubes formula
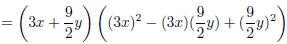 sub back in a = 3x and
sub back in a = 3x and 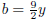
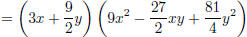 simplify
simplify
I would accept the above since it is factored, but
remember that you can sometimes write a factored form in different
ways. The following are all equivalent :
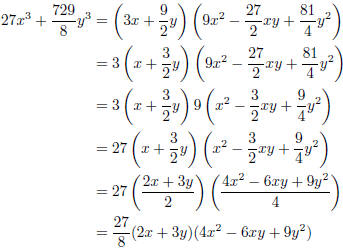
Example Factor 9x2 − 42xy + 49y2.
Notice that the first term and last term look like squares:
9x2 = (3x)2 = a2 (so a = 3x) and 49y2
= (7y)2 = b2 (so b = 7y).
Check if the middle term is 2ab = 2(3x)(7y) = 42xy. Yes! So this is a perfect
square (difference).
9x2 − 42xy + 49y2 = a2 − 2ab + b2
identify as a perfect square (difference)
![]() = (a − b)2 perfect square (difference) formula
= (a − b)2 perfect square (difference) formula
![]() = (3x − 7y)2 sub back in a = 3x and b = 7y.
= (3x − 7y)2 sub back in a = 3x and b = 7y.
Example Factor 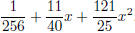
Notice that the first term and last term look like squares:
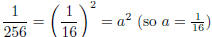 and
and
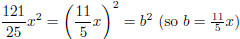
Check if the middle term is
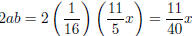 .Yes! So this is a perfect square (sum).
.Yes! So this is a perfect square (sum).
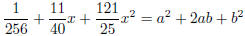 identify as a perfect
square (sum)
identify as a perfect
square (sum)
![]() = (a + b)2 perfect square (sum) formula
= (a + b)2 perfect square (sum) formula
![]()
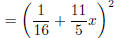 sub back in
sub back in
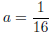 and
and 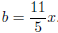
Example Factor 16x4 − 1.
16x4 − 1 =(4x2 )2− (1)2 rewrite to
see if it is a difference of squares
 = (a)2 − (b)2 Identify as difference of squares, a = 4x2,
b = 1
= (a)2 − (b)2 Identify as difference of squares, a = 4x2,
b = 1
 = (a + b)(a − b) write down memorized formula
= (a + b)(a − b) write down memorized formula
 = (4x2 + 1)(4x2 − 1) substitute back values for a = 4x2
and b = 1
= (4x2 + 1)(4x2 − 1) substitute back values for a = 4x2
and b = 1
 = (4x2 + 1)((2x)2 − (1)2) first polynomial is prime;
second is a difference of squares, a = 2x, b = 1
= (4x2 + 1)((2x)2 − (1)2) first polynomial is prime;
second is a difference of squares, a = 2x, b = 1
 = (4x2 + 1)(a + b)(a − b) write down memorized formula
= (4x2 + 1)(a + b)(a − b) write down memorized formula
 = (4x2 + 1)(2x + 1)(2x − 1) substitute back values for a = 2x and b =
1
= (4x2 + 1)(2x + 1)(2x − 1) substitute back values for a = 2x and b =
1
Example Factor 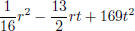 .
.
Notice that the first term and last term look like squares:
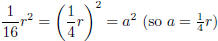 and 169t2 = (13t)2 = b2
(so b = 13t).
and 169t2 = (13t)2 = b2
(so b = 13t).
Check if the middle term is 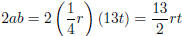 . Yes! So this is
a perfect square (difference).
. Yes! So this is
a perfect square (difference).
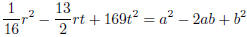 identify as a perfect square (difference)
identify as a perfect square (difference)
![]() = (a − b)2 perfect square (difference) formula
= (a − b)2 perfect square (difference) formula
![]()
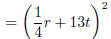 sub back in
sub back in 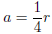 and b = 13t.
and b = 13t.
A Prime Polynomial is a polynomial that cannot be factored
using the techniques we developed here. For now, we are
concerned with integers, so something like x2 −3 would be considered
a prime polynomial even though we can write it as
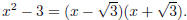
In practice you aren’t told which factoring technique to use, so being able to
recognize the different cases is important.
Using Factoring to Solve Equations
Zero factor property: If a · b = 0, then a = 0 or b = 0.
Solve quadratic equations by factoring:
2x2 + x − 10 = 0
Look for two numbers whose product is −20 and sum is +1: +5,−4
2x2 + 5x − 4x − 10 = 0
x(2x + 5) − 2(2x − 5) = 0
(x − 2)(2x + 5) = 0
x − 2 = 0 or 2x + 5 = 0
x = 2 or x = −5/2
A very common error in solving quadratic equations ax 2 + bx + c = 0
is to try to “isolate” the x (since this is what you
did for linear equations ). This is entirely the wrong way to proceed, and will
not lead you to the solution.
What this error looks like is the following:
3x2 + 5x + 2 = 0 ( equation we want to solve for x)
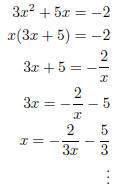
and so on. These steps are all mathematically correct, but
they will not lead to the solution since your goal when solving
a quadratic equation is not to isolate the x. Compare the above to a correct
solution that uses factoring:
3x2 + 5x + 2 = 0 (equation we want to solve for x)
 (factor
by grouping method: need two numbers whose product is 6 and sum is 5: 2 and 3)
(factor
by grouping method: need two numbers whose product is 6 and sum is 5: 2 and 3)
3x2 + 2x + 3x + 2 = 0 (rewrite middle term using 2 and 3)
x(3x + 2) + (3x + 2) = 0 (common factor in terms)
(x + 1)(3x + 2) = 0 (factor by grouping)
(x + 1) = 0 or (3x + 2) = 0 (zero factor property)
x = −1 or 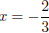 (simplify)
(simplify)
Application: Falling Objects When an object is
thrown straight upwards, it’s height S in meters is given by the
quadratic equation
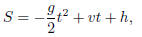
where g = acceleration due to gravity, which is 9.8m/s2
 v = initial upward velocity of the object in m/s
v = initial upward velocity of the object in m/s
 h = height above ground from which the object is thrown in meters
h = height above ground from which the object is thrown in meters
 t = time in seconds
t = time in seconds
This mathematical model of a physical system assumes there is no wind resistance
(among other things). We often
approximate the model as
S = −5t2 + vt + h.
Example Jon is in a baseball park outfield stands (right by the field), and he
throws a ball straight up in the air with all
his might. It leaves his hand with a velocity of 13 m/s, and at a height of 6 m
above the field. How long will it take the
ball to land on the field?
Solution : The ball hits the field when S = 0, and we also have v = 13 m/s and h
= 6 m, so we need to solve
0 = −5t2 + 13t + 6 (grouping method: need two numbers whose product is −30 and
sum is 13: 15 and −2)
0 = −5t2 + 15t − 2t + 6 (rewrite middle term using 15 and −2)
0 = 5t(−t + 3) + 2(−t + 3) (common factors in terms)
0 = (5t + 2)(−t + 3) (factor by grouping)
(5t + 2) = 0 or (−t + 3) = 0 (zero factor property)
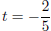 or t = 3 (simplify)
or t = 3 (simplify)
Exclude the negative answer as unphysical, and we see the ball hits the field
after 3 seconds.
Example You are standing on a cliff overlooking the ocean. You are 180 meters
above the ocean. You drop a pebble into
the ocean (dropping implies the initial velocity is 0 m/s). How long will it
take for the pebble to hit the water?
Solution: The pebble hits the water when S = 0, and we also have v = 0 m/s and h
= 180 m, so we need to solve
0 = −5t2 + 180
0 = −5(t2 − 36) (common factors in terms)
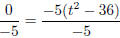 (divide each side by −5)
(divide each side by −5)
0 = t2 − 36 (difference of squares)
0 = (t − 6)(t + 6)
(t − 6) = 0 or (t + 6) = 0 (zero factor property)
t = 6 or t = −6 (simplify)
Exclude the t = −6 as unphysical, and we see the pebble hits the water after 6
seconds.
Example Factor 3x3a3 − 11x4a2
− 20x5a.
(common factors in terms) 3x3a3 − 11x4a2 −
20x5a = x3a(3a2 − 11xa − 20x2)
To factor 3a2 − 11xa − 20x2 we can treat this one of two
ways:
1. As a quadratic in x: −20x2 − 11ax + 3a2
2. As a quadratic in a: 3a2 − 11xa − 20x2
Let’s do the first, and see what happens. Let a tag along as if it was a number,
and use the grouping method.
The grouping number is (−20)(3a2) = −60a2.
Find two numbers whose product is −60a2 and whose sum is −11a: −15a
and 4a.
We will use these numbers to rewrite the middle term.
−20x2 − 11xa + 3a2 = −20x2 − 15ax + 4ax + 3a2
 = −5x(4x + 3a) + a(4x + 3a)
= −5x(4x + 3a) + a(4x + 3a)
![]() (common factors in terms)
(common factors in terms)
 = (−5x + a)(4x + 3a)
= (−5x + a)(4x + 3a)![]() (factor by grouping)
(factor by grouping)
Putting this back, we have determined that
3x3a3 − 11x4a2 − 20x5a = x3a(−5x +
a)(4x + 3a).
Example The area of a triangle is 3 ft2. The height is 10 ft longer than 4 times
the base. Determine the dimensions of
the triangle.
Let x be the length of the base. Then the height is equal to 4x + 10.
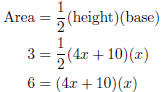
4x2 + 10x − 6 = 0 Two numbers: product −24, sum is 10: 12,−2
4x2 + 12x − 2x − 6 = 0
4x(x + 3) − 2(x + 3) = 0
(4x − 2)(x + 3) = 0
4x − 2 = 0 or x + 3 = 0
x = 1/2 or x = −3
Exclude the x = −3 as unphysical, and the dimensions of the triangle are base =
1/2 ft, and height = 4(1/2) + 10 = 12
ft.
Example By Dividing a − b into a3 − b3,
verify the formula a3 − b3 = (a − b)(a2 + ab +
b2).
Before we can divide, we have to include missing terms: a3 − b3
= a3 + 0a2b + 0ab2 − b3.

This shows that
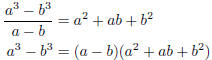
Example Factor x4 − y4.
x4 − y4 =(x2 )2
− (y2)2 rewrite to see if it is a difference of squares
= (a)2 − (b)2 Identify as difference of squares, a = x2, b = y2
= (a + b)(a − b) write down memorized formula
= (x2 + y2)(x2 − y2) substitute back
values for a = x2 and b = y2
= (x2 + y2)(x2 − y2) first
polynomial is prime; second is a difference of squares, a = x, b = y
= (x2 + y2)(a + b)(a − b) write down memorized formula
= (x2 + y2)(x + y)(x − y) substitute back values for a = x
and b = y
| Prev | Next |