FUNDAMENTAL TRIGONOMETRIC IDENTITIES
Reciprocal Identities
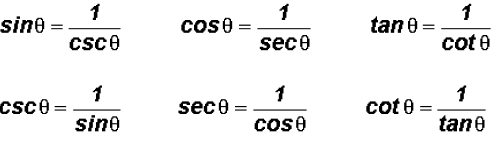
Quotient Identities

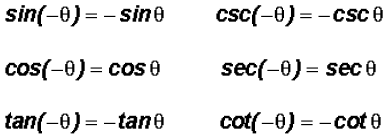
Pythagorean Identities
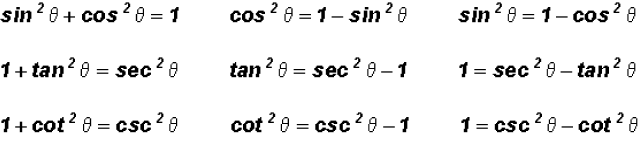
Problem 1:
Add or subtract the following trigonometric expressions:
(a) 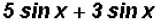
Since both terms have a sin x factor, we only have to add the coefficients.
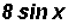
(b) 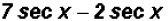
Since both terms have a sec x factor, we only have to subtract the
coefficients.
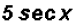
(c) 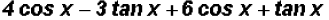
Here we combine the terms containing cos x and the terms containing tan x.
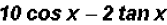
(d) 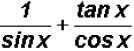
the common denominator is 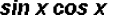
to add the two fractions the number 1 has to be
multiplied by cos x and the
expression tan x by sin x, and finally we get
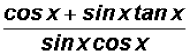
(e) 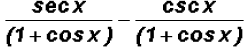
both fractions already have the same denominator, therefore
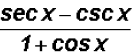
(f) 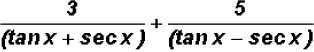
the common denominator is
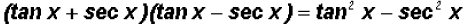
to add the two fractions, the number 3 has to be multiplied by (tan x
- sec x)
and the number 5 by (tan x + sec x)
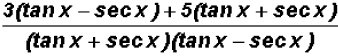
and multiplying out the numerator and combining like terms, we finally get
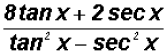
Problem 2:
Multiply the following trigonometric expressions :
(a)
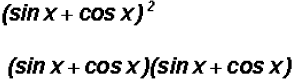
Now we will use FOIL to expand as follows :
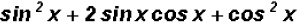
(b) 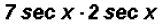
Here we will multiply the coefficients and the trigonometric ratios to get
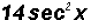
(c) 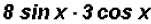
Here we will multiply the coefficients and the trigonometric ratios to get
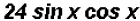
Problem 3:
Factor the following trigonometric expressions:
(a) 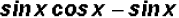
Notice that every term contains a factor of sin x which
can be factored out as
follows:

(b) 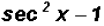
Notice that we are dealing with a the Difference of
Squares and we can factor
as follows:
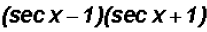
(c) 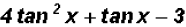
Factor the following expression just like the trinomial
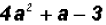 , that is,
, that is,
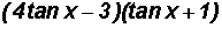
Problem 4:
Change the fraction 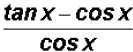 to two terms and
reduce.
to two terms and
reduce.
Note: You cannot cancel out cos x in the fraction
above. Only factors can
be canceled in rational expressions.
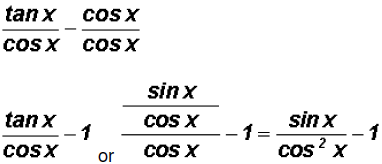
Problem 5:
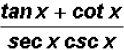 can be reduced to a
single number. Find this number.
can be reduced to a
single number. Find this number.
What could we do?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? YES
We can use Reciprocal Identities to rewrite tangent,
cotangent, secant, and
cosecant as follows:
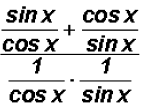
NOTE: While this is certainly a good start, it does not
guarantee
success. We might have to give up and think of something else to
do! If you are wondering if you are ever going to have to use this,
wait until you get to calculus. It is often much easier to reduce a
"complicated" trigonometric expression to a single trigonometric
ratio when working with calculus concepts.
Since we learned in algebra to always simplify complex
fractions, we will
multiply both the numerator and the denominator by the LCD sin x cos x
just
like we used to do in algebra.
But before we do this, let's combine the fractions in the
numerator of the
complex fraction as follows:
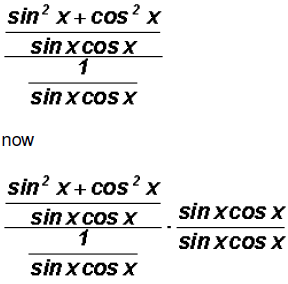
Next, we will distribute and at the same time reduce just
like we learned in
algebra to get
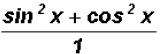
Now what?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? YES
We know that 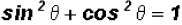 (Pythagorean Identity), therefore,
(Pythagorean Identity), therefore,
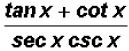 can be reduced to the number 1.
can be reduced to the number 1.
Problem 6:
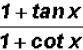 can be reduced
to a single trigonometric ratio, such as cos(x), sin(x), tan(x),
can be reduced
to a single trigonometric ratio, such as cos(x), sin(x), tan(x),
sec(x), csc(x), or cot(x). Find this ratio.
What could we do?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? YES
We can use Reciprocal Identities to rewrite tangent and cotangent as follows:
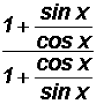
Since we learned in algebra to always simplify complex
fractions, we will
multiply both the numerator and the denominator by the LCD sin x cos x
just
like we used to do in algebra.
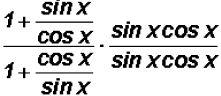
Next, we will distribute and at the same time reduce just
like we learned in
algebra to get
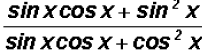
Now what?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? YES
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? NO
Let's factor common factors out of the numerator and the
denominator for a
lack of anything better to do.
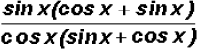
As you can see, the numerator and denominator have a
factor in common and
when reduced we end up with
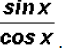 . Finally, we do know
that this equals
. Finally, we do know
that this equals 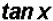 .
.
Therefore, we were able to reduce
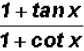 to the single trigonometric ratio
to the single trigonometric ratio
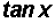 .
.
Problem 7:
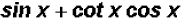 can be reduced to a
single trigonometric ratio, such as cos(x), sin
can be reduced to a
single trigonometric ratio, such as cos(x), sin
(x), tan(x), sec(x), csc(x), or cot(x). Find this ratio.
First, we will use 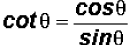 to
rewrite the expression as
to
rewrite the expression as 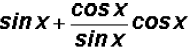 .
.
This is also equal to 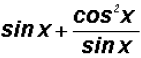 .
.
For a lack of anything better to do, let's write the last
expression as a single fraction.
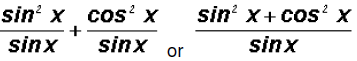
We see that we have the Pythagorean Identity
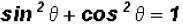 in the numerator, so
in the numerator, so
that we can replace it with 1 to get
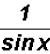 which equals
which equals
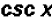 .
.
Problem 8:
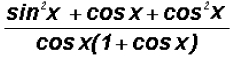 can be reduced to a
single trigonometric ratio, such as cos
can be reduced to a
single trigonometric ratio, such as cos
(x), sin(x), tan(x), sec(x), csc(x), or cot(x). Find this ratio.
Recognizing the Pythagorean Identity
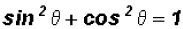 in the numerator, we can
in the numerator, we can
change the expression as follows:
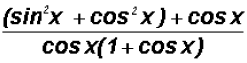
which also equals 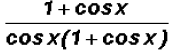
Lastly, we can cancel out the expression
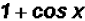 since it occurs both in the numerator
since it occurs both in the numerator
and in the denominator to find 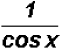 which equals
which equals
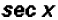 .
.
Problem 9:
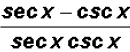 can be reduced to a
difference of two trigonometric ratios. Find this
can be reduced to a
difference of two trigonometric ratios. Find this
difference.
What could we do?
1. Add or subtract trigonometric expressions? NO
2. Multiply trigonometric expressions? NO
3. Factor trigonometric expressions? NO
4. Separate rational trigonometric expressions? NO
5. Use fundamental identities to rewrite an expression? YES
We can use Reciprocal Identities to rewrite secant and cosecant as follows:
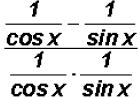
Since we learned in algebra to always simplify complex
fractions, we will
multiply both the numerator and the denominator by the LCD sin x cos x
just
like we used to do in algebra.
But before we do this, let's combine the fractions in the
numerator of the
complex fraction as follows:
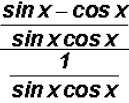
Please note that it is not mandatory to write sin x
as the first factor in the
product sin x cos x. However, it has become "unofficial" standard
practice
to do so!
Next,
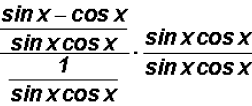
Finally, we will distribute and at the same time reduce
just like we learned in
algebra to get
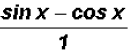
We find that 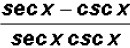 can be reduced to the difference
can be reduced to the difference
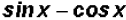 .
.
| Prev | Next |