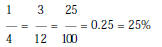Learning Standards for Mathematics

Mathematical Reasoning	Number and Numeration
1. Students use mathematical reasoning to analyze mathematical situations, make conjectures, gather evidence, and construct an argument. Students: • apply a variety of reasoning strategies. • make and evaluate conjectures and arguments using appropriate language. • make conclusions based on inductive reasoning. • justify conclusions involving simple and compound (i.e., and/or) statements. This is evident, for example, when students: use trial and error and work backwards to solve a problem. identify patterns in a number sequence. are asked to find numbers that satisfy two conditions, such as n > -4 and n ≤ 6.	2. Students use number sense and numeration to develop an understanding of the multiple uses of numbers in the real world , the use of numbers to communicate mathematically, and the use of numbers in the development of mathematical ideas. Students: • understand, represent, and use numbers in a variety of equivalent forms (integer, fraction, decimal, percent, exponential, expanded and scientific notation). • understand and apply ratios, proportions, and percents through a wide variety of hands-on explorations. • develop an understanding of number theory (primes, factors, and multiples). • recognize order relations for decimals, integers, and rational numbers. This is evident, for example, when students: use prime factors of a group of denominators to determine the least common denominator. select two pairs from a number of ratios and prove that they are in proportion. demonstrate the concept that a number can be symbolized by many different numerals as in:

Sample Problems


	Key ideas are identified by numbers (1). Performance indicators are identified by bullets (•). Sample tasks are identified by triangles ()

Students will understand mathematics and become mathematically confident by
communicating and reasoning mathematically, by applying mathematics in
real-world settings, and by solving problems through the integrated study of
number systems , geometry, algebra, data analysis, probability, and trigonometry

Operations

Modeling/Multiple
Representation

3. Students use mathematical operations and
relationships among them to understand mathematics.

Students:
• add, subtract, multiply, and divide fractions, decimals,
and integers.
• explore and use the operations dealing with roots and
powers .
• use grouping symbols (parentheses) to clarify the
intended order of operations.
• apply the associative, commutative, distributive, inverse,
and identity properties.
• demonstrate an understanding of operational algorithms
(procedures for adding, subtracting, etc.).
• develop appropriate proficiency with facts and
algorithms.
• apply concepts of ratio and proportion to solve problems.

This is evident, for example, when students:

create area models to help in understanding fractions, decimals,
and percents.

find the missing number in a proportion in which three of the
numbers are known, and letters are used as place holders.
s arrange a set of fractions in order, from the smallest to the
largest:

3 1 2 1 1
—, —, —, —, —
4 5 3 2 4

illustrate the distributive property for multiplication over
addition, such as

2(a + 3) = 2a + 6.

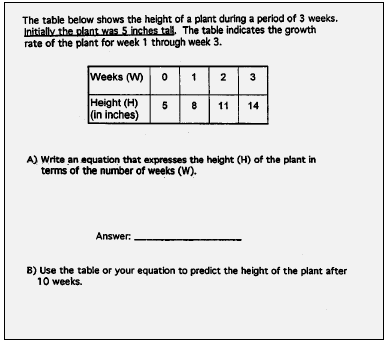
4. Students use mathematical modeling/multiple
representation to provide a means of presenting,
interpreting, communicating, and connecting
mathematical information and relationships.

Students:

• visualize, represent, and transform two- and three-dimensional
shapes.
• use maps and scale drawings to represent real objects or
places.
• use the coordinate plane to explore geometric ideas.
• represent numerical relationships in one- and two-dimensional
graphs.
• use variables to represent relationships.
• use concrete materials and diagrams to describe the
operation of real world processes and systems.
• develop and explore models that do and do not rely on
chance.
• investigate both two- and three-dimensional
transformations.
• use appropriate tools to construct and verify geometric
relationships.
• develop procedures for basic geometric constructions.

This is evident, for example, when students:

build a city skyline to demonstrate skill in linear measurements,
scale drawing, ratio, fractions, angles, and geometric shapes.

bisect an angle using a straight edge and compass.

draw a complex of geometric figures to illustrate that the
intersection of a plane and a sphere is a circle or point .

Sample Problems

Measurement	Uncertainty
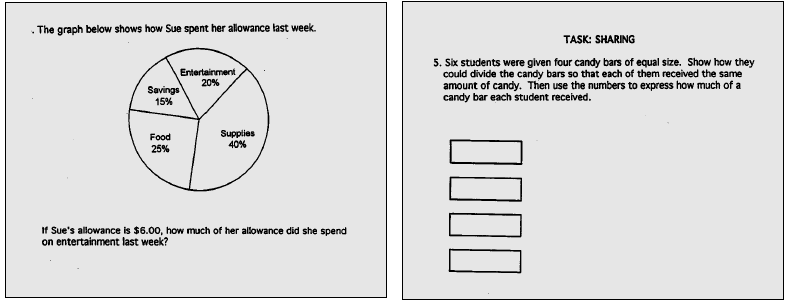
5. Students use measurement in both metric and English measure to provide a major link between the abstractions of mathematics and the real world in order to describe and compare objects and data. Students: • estimate, make, and use measurements in real-world situations. • select appropriate standard and nonstandard measurement units and tools to measure to a desired degree of accuracy. • develop measurement skills and informally derive and apply formulas in direct measurement activities. • use statistical methods and measures of central tendencies to display, describe, and compare data. • explore and produce graphic representations of data using calculators/computers. • develop critical judgment for the reasonableness of measurement. This is evident, for example, when students: use box plots or stem and leaf graphs to display a set of test scores. estimate and measure the surface areas of a set of gift boxes in order to determine how much wrapping paper will be required. explain when to use mean, median, or mode for a group of data.	6. Students use ideas of uncertainty to illustrate that mathematics involves more than exactness when dealing with everyday situations. Students: • use estimation to check the reasonableness of results obtained by computation, algorithms, or the use of technology. • use estimation to solve problems for which exact answers are inappropriate. • estimate the probability of events. • use simulation techniques to estimate probabilities. • determine probabilities of independent and mutually exclusive events. This is evident, for example, when students: construct spinners to represent random choice of four possible selections. perform probability experiments with independent events (e.g., the probability that the head of a coin will turn up, or that a 6 will appear on a die toss). estimate the number of students who might chose to eat hot dogs at a picnic.

Sample Problems

Students will understand mathematics and become mathematically confident by
communicating and reasoning mathematically, by applying mathematics in
real-world settings, and by solving problems through the integrated study of
number systems, geometry, algebra , data analysis, probability, and trigonometry.

Patterns/Functions

7. Students use patterns and functions to develop
mathematical power, appreciate the true beauty of
mathematics, and construct generalizations that
describe patterns simply and efficiently.

Students:
• recognize, describe, and generalize a wide variety of
patterns and functions.
• describe and represent patterns and functional
relationships using tables, charts and graphs , algebraic
expressions , rules, and verbal descriptions.
• develop methods to solve basic linear and quadratic
equations.
• develop an understanding of functions and functional
relationships: that a change in one quantity (variable)
results in change in another.
• verify results of substituting variables.
• apply the concept of similarity in relevant situations.
• use properties of polygons to classify them.
• explore relationships involving points, lines, angles, and
planes.
• develop and apply the Pythagorean principle in the
solution of problems.
• explore and develop basic concepts of right triangle
trigonometry.
• use patterns and functions to represent and solve
problems.

This is evident, for example, when students:

find the height of a building when a 20-foot ladder reaches the
top of the building when its base is 12 feet away from the
structure.
investigate number patterns through palindromes (pick a 2- digit
number, reverse it and add the two—repeat the process until a
palindrome appears)

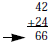
palindrome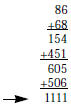

s solve linear equations, such as 2(x + 3) = x + 5 by several
methods.

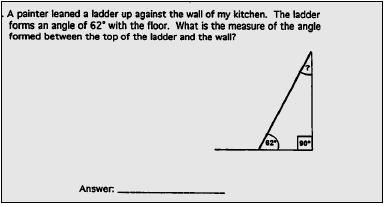
Sample Problem